Multivariate Time Series Analysis With Python for Forecasting and Modeling (Updated 2024)
Introduction
Time is the most critical factor in data science and machine learning, influencing whether a business thrives or falters. That’s why we see sales in stores and e-commerce platforms aligning with festivals. Businesses analyze multivariate time series of spending data over years to discern the optimal time to open the gates and witness a surge in consumer spending.
But how can you, as a data scientist, perform this analysis? Don’t worry, you don’t need to build a time machine! Time Series modeling is a powerful technique that acts as a gateway to understanding and forecasting trends and patterns.

But even a time series model has different facets. Most of the examples we see on the web deal with univariate time series. Unfortunately, real-world use cases don’t work like that. There are multiple variables at play, and handling all of them at the same time is where a data scientist will earn his worth.
Learning Objectives
- Understand what a multivariate time series is and how to deal with it.
- Understand the difference between univariate and multivariate time series.
- Learn the implementation of multivariate time series in Python following a case study-based tutorial.
Table of contents
Univariate Vs. Multivariate Time Series Forecasting Python
This article assumes some familiarity with univariate time series, their properties, and various techniques used for forecasting. Since this article will be focused on multivariate time series, I would suggest you go through the following articles, which serve as a good introduction to univariate time series:
- Comprehensive guide to creating time series forecast
- Build high-performance time series models using Auto Arima
But I’ll give you a quick refresher on what a univariate time series is before going into the details of a multivariate time series. Let’s look at them one by one to understand the difference.
Univariate Time Series
A univariate time series, as the name suggests, is a series with a single time-dependent variable.
For example, have a look at the sample dataset below, which consists of the temperature values (each hour) for the past 2 years. Here, the temperature is the dependent variable (dependent on Time).

If we are asked to predict the temperature for the next few days, we will look at the past values and try to gauge and extract a pattern. We would notice that the temperature is lower in the morning and at night while peaking in the afternoon. Also, if you have data for the past few years, you would observe that it is colder during the months of November to January while being comparatively hotter from April to June.
Such observations will help us in predicting future values. Did you notice that we used only one variable (the temperature of the past 2 years)? Therefore, this is called Univariate Time Series Analysis/Forecasting.
Multivariate Time Series (MTS)
A Multivariate time series has more than one time series variable. Each variable depends not only on its past values but also has some dependency on other variables. This dependency is used for forecasting future values. Sounds complicated? Let me explain.
Consider the above example. Suppose our dataset includes perspiration percent, dew point, wind speed, cloud cover percentage, etc., and the temperature value for the past two years. In this case, multiple variables must be considered to predict temperature optimally. A series like this would fall under the category of multivariate time series. Below is an illustration of this:
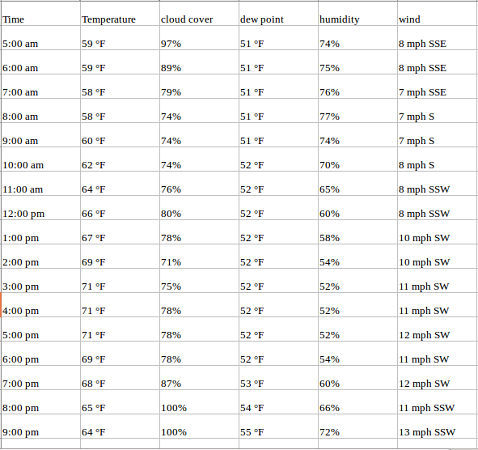
Now that we understand what a multivariate time series looks like, let us understand how we can use it to build a forecast.
Dealing With a Multivariate Time Series – VAR
In this section, I will introduce you to one of the most commonly used methods for multivariate time series forecasting – Vector Auto Regression (VAR).
In a VAR algorithm, each variable is a linear function of the past values of itself and the past values of all the other variables. To explain this in a better manner, I’m going to use a simple visual example:
We have two variables, y1, and y2. We need to forecast the value of these two variables at a time ‘t’ from the given data for past n values. For simplicity, I have considered the lag value to be 1.


To compute y1(t), we will use the past value of y1 and y2. Similarly, to compute y2(t), past values of both y1 and y2 will be used.
Simple mathematical way of representing this relation:
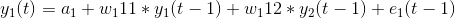

Here,
- a1 and a2 are the constant terms,
- w11, w12, w21, and w22 are the coefficients,
- e1 and e2 are the error terms
These equations are similar to the equation of an AR process. Since the AR process is used for univariate time series data, the future values are linear combinations of their own past values only. Consider the AR(1) process:
y(t) = a + w*y(t-1) +e
In this case, we have only one variable – y, a constant term – a, an error term – e, and a coefficient – w. In order to accommodate the multiple variable terms in each equation for VAR, we will use vectors. We can write equations (1) and (2) in the following form:

The two variables are y1 and y2, followed by a constant, a coefficient metric, a lag value, and an error metric. This is the vector equation for a VAR(1) process. For a VAR(2) process, another vector term for time (t-2) will be added to the equation to generalize for p lags:

The above equation represents a VAR(p) process with variables y1, y2 …yk. The same can be written as:


The term εt in the equation represents multivariate vector white noise. For a multivariate time series, εt should be a continuous random vector that satisfies the following conditions:
- E(εt) = 0
The expected value for the error vector is 0 - E(εt1,εt2‘) = σ12
The expected value of εt and εt‘ is the standard deviation of the series.
Why Do We Need Vector Autoregressive Models?
Recall the temperate forecasting example we saw earlier. An argument can be made for it to be treated as a multiple univariate series. We can solve it using simple univariate forecasting methods like AR. Since the aim is to predict the temperature, we can simply remove the other variables (except temperature) and fit a model on the remaining univariate series.
Another simple idea is to forecast values for each series individually using the techniques we already know. This would make the work extremely straightforward! Then why should you learn another forecasting technique? Isn’t this topic complicated enough already?
From the above equations (1) and (2), it is clear that each variable is using the past values of every variable to make predictions. Unlike AR, VAR is able to understand and use the relationship between several variables. This is useful for describing the dynamic behavior of the data and also provides better forecasting results. Additionally, implementing VAR is as simple as using any other univariate technique (which you will see in the last section).
The extensive usage of VAR models in finance, econometrics, and macroeconomics can be attributed to their ability to provide a framework for achieving significant modeling objectives. With VAR models, it is possible to elucidate the values of endogenous variables by considering their previously observed values.
Granger’s Causality Test
Granger’s causality test can be used to identify the relationship between variables prior to model building. This is important because if there is no relationship between variables, they can be excluded and modeled separately. Conversely, if a relationship exists, the variables must be considered in the modeling phase.
The test in mathematics yields a p-value for the variables. If the p-value exceeds 0.05, the null hypothesis must be accepted. Conversely, if the p-value is less than 0.05, the null hypothesis must be rejected.
Stationarity of a Multivariate Time Series
We know from studying the univariate concept that a stationary time series will, more often than not, give us a better set of predictions. If you are not familiar with the concept of stationarity, please go through this article first: A Gentle Introduction to handling non-stationary Time Series.
To summarize, for a given univariate time series:
y(t) = c*y(t-1) + ε t
The series is said to be stationary if the value of |c| < 1. Now, recall the equation of our VAR process:

Note: I is the identity matrix.
Representing the equation in terms of Lag operators, we have:

Taking all the y(t) terms on the left-hand side:


The coefficient of y(t) is called the lag polynomial. Let us represent this as Φ(L):


For a series to be stationary, the eigenvalues of |Φ(L)-1| should be less than 1 in modulus. This might seem complicated, given the number of variables in the derivation. This idea has been explained using a simple numerical example in the following video. I highly encourage watching it to solidify your understanding:
Similar to the Augmented Dickey-Fuller test for univariate series, we have Johansen’s test for checking the stationarity of any multivariate time series data. We will see how to perform the test in the last section of this article.
Train-Validation Split
If you have worked with univariate time series data before, you’ll be aware of the train-validation sets. The idea of creating a validation set is to analyze the performance of the model before using it for making predictions.
Creating a validation set for time series problems is tricky because we have to take into account the time component. One cannot directly use the train_test_split or k-fold validation since this will disrupt the pattern in the series. The validation set should be created considering the date and time values.
Suppose we have to forecast the temperate diff, dew point, cloud percent, etc., for the next two months using data from the last two years. One possible method is to keep the data for the last two months aside and train the model for the remaining 22 months.
Once the model has been trained, we can use it to make predictions on the validation set. Based on these predictions and the actual values, we can check how well the model performed and the variables for which the model did not do so well. And for making the final prediction, use the complete dataset (combine the training data and validation sets).
Python Implementation
In this section, we will implement the Vector AR model on a toy dataset. I have used the Air Quality dataset for this and you can download it from here.
Python Code
Preparing the Data
The data type of the Date_Time column is object, and we need to change it to datetime. Also, for preparing the data, we need the index to have datetime. Follow the below commands:
df['Date_Time'] = pd.to_datetime(df.Date_Time , format = '%d/%m/%Y %H.%M.%S')
data = df.drop(['Date_Time'], axis=1)
data.index = df.Date_TimeDeal with Missing Values
The next step is to deal with the missing values. It is not always wise to use df.dropna. Since the missing values in the data are replaced with a value of -200, we will have to impute the missing value with a better number. Consider this – if the present dew point value is missing, we can safely assume that it will be close to the value of the previous hour. That makes sense, right? Here, I will impute -200 with the previous value.
You can choose to substitute the value using the average of a few previous values or the value at the same time on the previous day (you can share your idea(s) of imputing missing values in the comments section below).
#missing value treatment
cols = data.columns
for j in cols:
for i in range(0,len(data)):
if data[j][i] == -200:
data[j][i] = data[j][i-1]
#checking stationarity
from statsmodels.tsa.vector_ar.vecm import coint_johansen
#since the test works for only 12 variables, I have randomly dropped
#in the next iteration, I would drop another and check the eigenvalues
johan_test_temp = data.drop([ 'CO(GT)'], axis=1)
coint_johansen(johan_test_temp,-1,1).eigBelow is the result of the test:
array([ 0.17806667, 0.1552133 , 0.1274826 , 0.12277888, 0.09554265,
0.08383711, 0.07246919, 0.06337852, 0.04051374, 0.02652395,
0.01467492, 0.00051835])Creating the Validation Set
We can now go ahead and create the validation set to fit the model and test its performance.
#creating the train and validation set
train = data[:int(0.8*(len(data)))]
valid = data[int(0.8*(len(data))):]
#fit the model
from statsmodels.tsa.vector_ar.var_model import VAR
model = VAR(endog=train)
model_fit = model.fit()
# make prediction on validation
prediction = model_fit.forecast(model_fit.y, steps=len(valid))Making it Presentable
The predictions are in the form of an array, where each list represents the predictions of the row. We will transform this into a more presentable format.
#converting predictions to dataframe
pred = pd.DataFrame(index=range(0,len(prediction)),columns=[cols])
for j in range(0,13):
for i in range(0, len(prediction)):
pred.iloc[i][j] = prediction[i][j]
#check rmse
for i in cols:
print('rmse value for', i, 'is : ', sqrt(mean_squared_error(pred[i], valid[i])))Output:
rmse value for CO(GT) is : 1.4200393103392812
rmse value for PT08.S1(CO) is : 303.3909208229375
rmse value for NMHC(GT) is : 204.0662895081472
rmse value for C6H6(GT) is : 28.153391799471244
rmse value for PT08.S2(NMHC) is : 6.538063846286176
rmse value for NOx(GT) is : 265.04913993413805
rmse value for PT08.S3(NOx) is : 250.7673347152554
rmse value for NO2(GT) is : 238.92642219826683
rmse value for PT08.S4(NO2) is : 247.50612831072633
rmse value for PT08.S5(O3) is : 392.3129907890131
rmse value for T is : 383.1344361254454
rmse value for RH is : 506.5847387424092
rmse value for AH is : 8.139735443605728After the testing on the validation set, let’s fit the model on the complete dataset.
#make final predictions
model = VAR(endog=data)
model_fit = model.fit()
yhat = model_fit.forecast(model_fit.y, steps=1)
print(yhat)We can test the performance of our model by using the following methods:
- Akaike information criterion (AIC): It quantifies the quality of a model by balancing the fit of the model to the data with the complexity of the model. AIC provides a way to compare different models and choose the one that best fits the data with the least complexity.
- Bayesian information criterion (BIC): This stats measure is used for model selection among a set of candidate models. Like the Akaike information criterion (AIC), BIC provides a trade-off between the goodness of fit and model complexity. However, BIC places a stronger penalty on the number of parameters than AIC does, which can help prevent overfitting.
Conclusion
Before I started this article, the idea of working with a multivariate time series seemed daunting in its scope. It is a complex topic, so take your time to understand the details. The best way to learn is to practice, so I hope the above Python implementations will be useful for you.
I encourage you to use this approach on a dataset of your choice. This will further cement your understanding of this complex yet highly useful topic. If you have any suggestions or queries, share them in the comments section.
Key Takeaways
- Multivariate time series analysis involves the analysis of data over time that consists of multiple interdependent variables.
- Vector Auto Regression (VAR) is a popular model for multivariate time series analysis that describes the relationships between variables based on their past values and the values of other variables.
- VAR models can be used for forecasting and making predictions about the future values of the variables in the system.
Frequently Asked Questions
A. Vector Auto Regression (VAR) model is a statistical model that describes the relationships between variables based on their past values and the values of other variables. It is a flexible and powerful tool for analyzing interdependencies among multiple time series variables.
A. The order of a VAR model specifies the number of lags used in the model. It determines how many past observations of the variables are included in the model. The order is usually determined using information criteria such as AIC and BIC.
A. Granger causality tests can be used to determine whether one variable is useful in predicting another variable in a VAR model. It involves testing whether the inclusion of lagged values of one variable in a VAR model improves the forecasting accuracy of another variable.











HI. Thanks for sharing the knowledge and the great article! Could you pls add some details regarding the stationarity test process described in the article : the test is done and the results are presented but it is not clear if it could be concluded that the data is stationary; after the test is done no further actions to make the data stationary are performed...why so. Thanks
Why not just use Random Forest for this? Thank you
Hi John, random forest can be used for supervised machine learning algorithms. In this case, we don't have a test set. Considering the example for weather prediction used in section 1 -if you consider temperature as target variable and the rest as independent variables, the test set must have the independent variables, which is not the case here. Using VAR , we predict all the variables .
Hi Alex, under the stationarity section, we understood that if the modulus of eigenvalues are less than 1, the series would be classified as stationary. While implementation, since the condition is satisfied, I have not performed any transformation on the series. There is a complete article that describes dealing with non stationary time series (link provided in this article).
I have to face the same type of problem. I have one target variable and other rests of variables are independent. Data is given day to day time series observation. Now I want to forecast the target variable for the next three months. It is helpful if you share this type of article.
Hi , I have applied the coint_johansen on my dataset. But , since most of the dependent variables are 0 , I am getting Singular Matrix error. How can I solve it ?
Hi, Please share the notebook. Have dropped the mail
Can you give the csv used in this?
The csv file is shared in the post itself. Refer section 6 of the article.
Hi Aish, Thanks for the great article. Could you pl explain how a VAR and ECM differentiate. Thx
Hi, I haven't worked with ECM yet. You can probably put the question on discuss.analyticsvidhya.com so that the community can help you clarify the doubt.
Hi! I was wondering about ranges of each column of the dataset. VAR models express every output as a linear combination of other variables weighted in a certain way. So, using absolute values changing in different ranges is probably not a good solution. RMSE high values seem to confirm this. Am I wrong?
That's a good point. Normalizing should reduce the rmse value. Have you tried applying it on this dataset?
#missing value treatment cols = data.columns for j in cols: for i in range(0,len(data)): if data[j][i] == -200: data[j][i] = data[j][i-1] the above code can be replaced with data = data.fillna(method='ffill') http://pandas.pydata.org/pandas-docs/stable/generated/pandas.DataFrame.fillna.html
Hi, Thanks a lot for the great article! I guess, the Python implementation was done in Python 2.3. I am using Python 3.0 and getting the below exception while replacing the missing values and checking the stationarity part. #missing value treatment cols = data.columns for j in cols: for i in range(0,len(data)): if data[j][i] == -200: data[j][i] = data[j][i-1] #checking stationarity from statsmodels.tsa.vector_ar.vecm import coint_johansen #since the test works for only 12 variables, I have randomly dropped #in the next iteration, I would drop another and check the eigenvalues johan_test_temp = data.drop(['CO(GT)'], axis=1) coint_johansen(johan_test_temp,-1,1).eig Error:- A value is trying to be set on a copy of a slice from a DataFrame [Warning] TypeError: unsupported operand type(s) for -: 'str' and 'str' Can you please help me solving the error? Also, could you please provide me the O/P (few lines) of the below line:- # make prediction on validation prediction = model_fit.forecast(model_fit.y, steps=len(valid)) Thanks a lot.
Hello, It was a very instructive article, I have a question on your final prediction. Why do you fit a new VAR model on your whole dataset to make your prediction instead of taking the previous fitted model (with your training set) ? Thank you very much
Hi Rick, We build a new model for two reasons - Firstly, we must train the model on the complete set otherwise we loose some information. Secondly, the model makes prediction for dates after the training data. If we use only the train set, the predictions will be for dates present on the validation set.
Hi, Thank you for the tutorial, i want to ask you please about this line : # make prediction on validation prediction = model_fit.forecast(model_fit.y, steps=len(valid)) what does y in model_fit.y mean ? and can we apply this approach (test of stationnarity+VAR) if we have just 2 variables both of them dependent to time thank you so much
Hi Soukaina,
prediction = model_fit.forecast(model_fit.y, steps=len(valid))We first fit the model on the data and then forecast values for the length of validation set.Hello, The article is really great! I have understood the mathematics and reasoning behind the VAR, however, I still have a problem in compiling the same in python and I need basic codes for the same. Please help me regarding the same. Thank you very much.
Hey Parth, The complete code is given in the article itself. Let me know which part are you facing an issue with.
Hello Aishwarya I have 2 datasets that contains weather data, air pollution data, and all the variables measures in hours. How can I study the correlation between variables to do the features selection. I do not need all the variables in ny module,I need to identify the air pollution variables that effected by the weather variables How could i do that?
Hi Maya, You can use the
data.corr()function to get the correlation between the variables. You can then select or remove the variables.df = pd.read_csv("AirQualityUCI.csv", parse_dates=[['Date', 'Time']]); i have problem with parse_date function he doeesn't work. Can i have another fufnction which can permit to parse 'Date' and 'Time' ?
Hi, You can read the dataset without using parse_dates, and then later convert the datatype of column from object to datetime using the pd.to_datetime function.
Run as df = pd.read_csv("AirQualityUCI.csv",decimal=',',delimiter=';',parse_dates=[['Date', 'Time']])
Hi Aishwarya, in this part: prediction = model_fit.forecast(model_fit.y, steps=len(valid)) how will the model perceive that it has to forecast for the values in the Valid data, also how can we check the accuracy?
Hi there, this is extremely helpful and thank you for easy explanation. Im trying to model a house price prediction based on many independent economic variables, do you think this multi VAR model will work better than a multi ARIMA model ?
Great article I really enjoyed it. I wish it would have went a few steps further like appending the results to the original data frame then doing some charting or visualizations of the predictions.
How can i visualise the results?
You can use the matplot library. Simply plot the actual values and the predictions on the same plot to compare.
Hi Aishwarya, I've to make my data stationary as the values of it are higher than 1 when performed Johansen’s test. Can you provide any resource how to make data stationary. Thanks
Hello Aishwarya, I have some doubt please help me out, in my data set there is test data and I want to predict for the test data but in my test data there is no dependent variable so how to predict for the test data? Thank You.
Hi Prabin, You can go for other forecasting techniques like the ARIMA model or SARIMA model
Hey, I applied this technique on a Stock market data set that I'm using, this sounds perfect for the same since we do not have the metric values like (open,close,volume) etc when you predict for the future. My issue is when I put a time step greater than 4 yhat = model_fit.forecast(model_fit.y, steps=4) I get values as this [[ 1.17209033e+03 1.18086615e+03 1.16135799e+03 1.17042778e+03 -6.06615633e+03] [ 1.17046801e+03 1.17967174e+03 1.16002395e+03 1.17002167e+03 -5.08440819e+05] [ 1.17000230e+03 1.17913784e+03 1.15954912e+03 1.16943372e+03 -9.05551651e+05] [ 1.16941661e+03 1.17854065e+03 1.15899300e+03 1.16887356e+03 -1.19753464e+06]] Is this because it is finding it hard to predict at that high of a time step? Thanks for the help!
Hi I am getting below error. please let me know how to fix it ValueWarning: No frequency information was provided, so inferred frequency MS will be used. % freq, ValueWarning) /home/dspl_user/.local/lib/python2.7/site-packages/statsmodels/tsa/base/tsa_model.py:191: FutureWarning: Creating a DatetimeIndex by passing range endpoints is deprecated. Use `pandas.date_range` instead.
Hello Aishwarya, I have data with two columns and 10000 rows, i want to predict next 1000 data, is it possible using VAR.
Hi Aishwarya, While fitting the VAR model on my fataframe I am getting the following error TypeError: unsupported operand type(s) for -: 'str' and 'str' kindly help!
Hello Have two variables and 100000 no's previous values . Is it possible to predict 1000 steps using VAR .
Hi, In my dataset time is UTC Format, so df['Date_Time'] = pd.to_datetime(df.Date_Time , format = '%d/%m/%Y %H.%M.%S') data = df.drop(['Date_Time'], axis=1) data.index = df.Date_Time when i usig this code i get error. any ather solution for this . Thankyou
Hi Aishwarya, So can I use the same approach where I want to predict consumable items? For example, if I want to predict how many alcohol bottles will be required in a given flight? For this, I have a past alcohol consumption, the current number of Passenger in a given flight and the season. What will be the best approach to predict consumption? Regards Ankur
Thanks for this post, now is my guide ;) Question: I have temperature in a period of time and also number of owls born (per month). The hypothesis is that the temperature influences on the number of owls born. With this model is possible to take into consideration not only the temperature of the current month, but also month -1, month -2 and so on? Thanks in advance for your guide
Hi Can you help how can i create ARIMA model for multivariate data?
Hi Aishwarya, Thank you for this brilliant post, 2 questions, and they might be very basic, so i apologize in advance. 1. How do you intrepret the results? you end up with a list of RMSEs but what do they mean?and how can i tell if a value is "good" or "bad"? 2. i saw you wrote that one could plot "Simply plot the actual values and the predictions on the same plot to compare" but the actual value is an input, and the predictions, as far as i understand are just the RMSE? Thank you
Hi Aishwarya, Thank you for this brilliant post, i have to questions, that might be very basic, so i apologize in advance. 1. How to you interpret the results you have? what are the meaning of the RMSEs you have? how do you know them to be "good" or "bed"? 2. how do you plot it? i saw you commented that you can "Simply plot the actual values and the predictions on the same plot to compare" but where do you get those prediction from? the "pred" df? Thank you Navot
Hi Aishwarya, many thanks for sharing the knowledge, its a great article. I now understand the time series forecasting using VAR. However I have a question. Is it possible to predict "temperature" for a specific day in the future and considering one of the dependent variables is at a specific value say CO. e.g what will be the temperature on 1st May at 9.00am if the CO is nn. ?
Hi, if I have to forecast Two wheeler demand, and in my test data i already have the predicted values of all the independent variables ( through analyst estimates for GDP, Monsoon, and other variables), do i still need to use VAR or i can fit multiple linear regression? Thanks
Hi! Thank you for the article. I have a specific situation for which I have not found an answer anywhere thusfar (as in my situation I do not explain my time series by their values in the previous time period [T-1]). I have a dataset of 5 variables, with one of the independent variables (global temperature anomaly) showing nonstationarity and the rest of my time series showing stationarity. I like to explain the local temperature (dependent variable) with the global temperature, 3 wind vector variables (west-east component, south-north and vorticity which is the upward speed of wind and used as a proxy for cloud cover) and lastly a memory term for local temperature. Since I do monthly regressions (meaning that I investigate only 1 particular month over a span of 60 years to remove seasonality, for example 1950-2010 for the month June ONLY) this memory term is not a lag term in the econometric sense, but the previous month. So in the mentioned example this would be May between 1950-2010. How do I proceed to make a statistically solid regression if one of my dependent variables is nonstationary and the rest is stationary? Like mentioned, I solely look to local temperature as explained by the independent variables at that same T, and i dont explain any of my variables with their lagged values in time period T-1 (as loc temperature in May for 1972 would not have any influence on loc temperature for May 1973 since there are a lot of time steps in between that I do not include in the regression). Thank you, any help would be greatly appreciated.
Hi Aishwarya, I am getting negative predicted sales values after applying pred function. Do I need to do any log transformation in my data before fitting it with VAR model. Please let me know how to tackle this situation?
Hi there! quick question what does the "(model_fit, steps=1)" mean in the code you used? make final predictions model = VAR(endog=data) model_fit = model.fit() yhat = model_fit.forecast(model_fit.y, steps=1) print(yhat)
Hi dear, thank you for this article, however I have some questions regarding the multivariate series. Will u pls. send an email at itzmediana@gmailcom, so that we could discuss this further?