Want to Generate your own Music using Deep Learning? Here’s a Guide to do just that!
Overview
- Learn how to develop an end-to-end model for Automatic Music Generation
- Understand the WaveNet architecture and implement it from scratch using Keras
- Compare the performance of WaveNet versus Long Short Term Memory for building an Automatic Music Generation model
Introduction
“If I were not a physicist, I would probably be a musician. I often think in music. I live my daydreams in music. I see my life in terms of music.” – Albert Einstein
I might not be a physicist like Mr. Einstein, but I wholeheartedly agree with his thoughts on music! I can’t remember a single day when I didn’t open up my music player. My travel to and from office is accompanied by the tune of music and honestly, it helps me focus on my work.
I’ve always dreamed of composing music but didn’t quite get the hang of instruments. That was until I came across deep learning. Using certain techniques and frameworks, I was able to compose my own original music score without really knowing any music theory!
This was one of my favorite professional projects. I combined my two passions – music and deep learning – to create an automatic music generation model. It’s a dream come true!
I am thrilled to share my approach with you, including the entire code to enable you to generate your own music! We’ll first quickly understand the concept of automatic music generation before diving into the different approaches we can use to perform this. Finally, we will fire up Python and design our own automatic music generation model.
Table of Contents
- What is Automatic Music Generation?
- What are the Constituent Elements of Music?
- Different Approaches to Music Generation
- Using WaveNet Architecture
- Using Long Short Term Memory (LSTM)
- Implementation – Automatic Music Composition using Python
What is Automatic Music Generation?
Music is an Art and a Universal language.
I define music as a collection of tones of different frequencies. So, the Automatic Music Generation is a process of composing a short piece of music with minimum human intervention.
What could be the simplest form of generating music?
It all started by randomly selecting sounds and combining them to form a piece of music. In 1787, Mozart proposed a Dice Game for these random sound selections. He composed nearly 272 tones manually! Then, he selected a tone based on the sum of 2 dice.
Another interesting idea was to make use of musical grammar to generate music.
Musical Grammar comprehends the knowledge necessary to the just arrangement and combination of musical sounds and to the proper performance of musical compositions
– Foundations of Musical Grammar
In the early 1950s, Iannis Xenakis used the concepts of Statistics and Probability to compose music – popularly known as Stochastic Music. He defined music as a sequence of elements (or sounds) that occurs by chance. Hence, he formulated it using stochastic theory. His random selection of elements was strictly dependent on mathematical concepts.
Recently, Deep Learning architectures have become the state of the art for Automatic Music Generation. In this article, I will discuss two different approaches for Automatic Music Composition using WaveNet and LSTM (Long Short Term Memory) architectures.
Note: This article requires a basic understanding of a few deep learning concepts. I recommend going through the below articles:
- A Comprehensive Tutorial to learn Convolutional Neural Networks (CNNs) from Scratch
- Essentials of Deep Learning: Introduction to Long Short Term Memory (LSTM)
- Must-Read Tutorial to Learn Sequence Modeling
What are the Constituent Elements of Music?
Music is essentially composed of Notes and Chords. Let me explain these terms from the perspective of the piano instrument:
- Note: The sound produced by a single key is called a note
- Chords: The sound produced by 2 or more keys simultaneously is called a chord. Generally, most chords contain at least 3 key sounds
- Octave: A repeated pattern is called an octave. Each octave contains 7 white and 5 black keys
Different Approaches to Automatic Music Generation
I will discuss two Deep Learning-based architectures in detail for automatically generating music – WaveNet and LSTM. But, why only Deep Learning architectures?
Deep Learning is a field of Machine Learning which is inspired by a neural structure. These networks extract the features automatically from the dataset and are capable of learning any non-linear function. That’s why Neural Networks are called as Universal Functional Approximators.
Hence, Deep Learning models are the state of the art in various fields like Natural Language Processing (NLP), Computer Vision, Speech Synthesis and so on. Let’s see how we can build these models for music composition.
Approach 1: Using WaveNet
WaveNet is a Deep Learning-based generative model for raw audio developed by Google DeepMind.
The main objective of WaveNet is to generate new samples from the original distribution of the data. Hence, it is known as a Generative Model.
Wavenet is like a language model from NLP.
In a language model, given a sequence of words, the model tries to predict the next word. Similar to a language model, in WaveNet, given a sequence of samples, it tries to predict the next sample.
Approach 2: Using Long Short Term Memory (LSTM) Model
Long Short Term Memory Model, popularly known as LSTM, is a variant of Recurrent Neural Networks (RNNs) that is capable of capturing the long term dependencies in the input sequence. LSTM has a wide range of applications in Sequence-to-Sequence modeling tasks like Speech Recognition, Text Summarization, Video Classification, and so on.
Let’s discuss in detail how we can train our model using these two approaches.
Wavenet: The Training Phase
This is a Many-to-One problem where the input is a sequence of amplitude values and the output is the subsequent value.
Let’s see how we can prepare input and output sequences.
Input to the WaveNet:
WaveNet takes the chunk of a raw audio wave as an input. Raw audio wave refers to the representation of a wave in the time series domain.
In the time-series domain, an audio wave is represented in the form of amplitude values which are recorded at different intervals of time:
Output of the WaveNet:
Given the sequence of the amplitude values, WaveNet tries to predict the successive amplitude value.
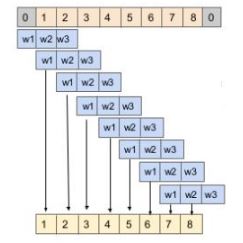
Let’s understand this with the help of an example. Consider an audio wave of 5 seconds with a sampling rate of 16,000 (that is 16,000 samples per second). Now, we have 80,000 samples recorded at different intervals for 5 seconds. Let’s break the audio into chunks of equal size, say 1024 (which is a hyperparameter).
The below diagram illustrates the input and output sequences for the model:

Input and Output of first 3 chunks
We can follow a similar procedure for the rest of the chunks.
We can infer from the above that the output of every chunk depends only on the past information ( i.e. previous timesteps) but not on the future timesteps. Hence, this task is known as Autoregressive task and the model is known as an Autoregressive model.
Inference phase
In the inference phase, we will try to generate new samples. Let’s see how to do that:
- Select a random array of sample values as a starting point to model
- Now, the model outputs the probability distribution over all the samples
- Choose the value with the maximum probability and append it to an array of samples
- Delete the first element and pass as an input for the next iteration
- Repeat steps 2 and 4 for a certain number of iterations
Understanding the WaveNet Architecture
The building blocks of WaveNet are Causal Dilated 1D Convolution layers. Let us first understand the importance of the related concepts.
Why and What is a Convolution?
One of the main reasons for using convolution is to extract the features from an input.
For example, in the case of image processing, convolving the image with a filter gives us a feature map.
Convolution is a mathematical operation that combines 2 functions. In the case of image processing, convolution is a linear combination of certain parts of an image with the kernel.
You can browse through the below article to read more about convolution:
What is 1D Convolution?
The objective of 1D convolution is similar to the Long Short Term Memory model. It is used to solve similar tasks to those of LSTM. In 1D convolution, a kernel or a filter moves along only one direction:
The output of convolution depends upon the size of the kernel, input shape, type of padding, and stride. Now, I will walk you through different types of padding for understanding the importance of using Dilated Causal 1D Convolution layers.
When we set the padding valid, the input and output sequences vary in length. The length of an output is less than an input:
When we set the padding to same, zeroes are padded on either side of the input sequence to make the length of input and output equal:
Pros of 1D Convolution:
- Captures the sequential information present in the input sequence
- Training is much faster compared to GRU or LSTM because of the absence of recurrent connections
Cons of 1D Convolution:
- When padding is set to the same, output at timestep t is convolved with the previous t-1 and future timesteps t+1 too. Hence, it violates the Autoregressive principle
- When padding is set to valid, input and output sequences vary in length which is required for computing residual connections (which will be covered later)
This clears the way for the Causal Convolution.
Note: The pros and Cons I mentioned here are specific to this problem.
What is 1D Causal Convolution?
This is defined as convolutions where output at time t is convolved only with elements from time t and earlier in the previous layer.
In simpler terms, normal and causal convolutions differ only in padding. In causal convolution, zeroes are added to the left of the input sequence to preserve the principle of autoregressive:
Pros of Causal 1D convolution:
- Causal convolution does not take into account the future timesteps which is a criterion for building a Generative model
Cons of Causal 1D convolution:
- Causal convolution cannot look back into the past or the timesteps that occurred earlier in the sequence. Hence, causal convolution has a very low receptive field. The receptive field of a network refers to the number of inputs influencing an output:
As you can see here, the output is influenced by only 5 inputs. Hence, the Receptive field of the network is 5, which is very low. The receptive field of a network can also be increased by adding kernels of large sizes but keep in mind that the computational complexity increases.
This drives us to the awesome concept of the Dilated 1D Causal Convolution.
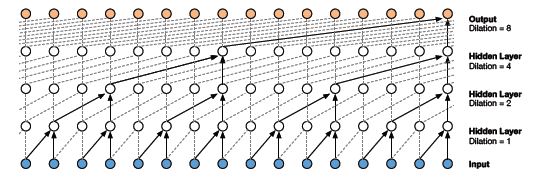
What is Dilated 1D Causal Convolution?
A Causal 1D convolution layer with the holes or spaces in between the values of a kernel is known as Dilated 1D convolution.
The number of spaces to be added is given by the dilation rate. It defines the reception field of a network. A kernel of size k and dilation rate d has d-1 holes in between every value in kernel k.
As you can see here, convolving a 3 * 3 kernel over a 7 * 7 input with dilation rate 2 has a reception field of 5 * 5.
Pros of Dilated 1D Causal Convolution:
- The dilated 1D convolution network increases the receptive field by exponentially increasing the dilation rate at every hidden layer:
As you can see here, the output is influenced by all the inputs. Hence, the receptive field of the network is 16.
Residual Block of WaveNet:
A building block contains Residual and Skip connections which are just added to speed up the convergence of the model:
The Workflow of WaveNet:
- Input is fed into a causal 1D convolution
- The output is then fed to 2 different dilated 1D convolution layers with sigmoid and tanh activations
- The element-wise multiplication of 2 different activation values results in a skip connection
- And the element-wise addition of a skip connection and output of causal 1D results in the residual
Long Short Term Memory (LSTM) Approach
Another approach for automatic music generation is based on the Long Short Term Memory (LSTM) model. The preparation of input and output sequences is similar to WaveNet. At each timestep, an amplitude value is fed into the Long Short Term Memory cell – it then computes the hidden vector and passes it on to the next timesteps.
The current hidden vector at timestep ht is computed based on the current input at and previously hidden vector ht-1. This is how the sequential information is captured in any Recurrent Neural Network:
Pros of LSTM:
- Captures the sequential information present in the input sequence
Cons of LSTM:
- It consumes a lot of time for training since it processes the inputs sequentially
Implementation – Automatic Music Generation using Python
The wait is over! Let’s develop an end-to-end model for the automatic generation of music. Fire up your Jupyter notebooks or Colab (or whichever IDE you prefer).
Download the Dataset:
I downloaded and combined multiple classical music files of a digital piano from numerous resources. You can download the final dataset from here.
Import libraries:
#library for understanding music from music21 import *
Reading Musical Files:
Let’s define a function straight away for reading the MIDI files. It returns the array of notes and chords present in the musical file.
Now, we will load the MIDI files into our environment
Understanding the data:
Under this section, we will explore the dataset and understand it in detail.
Output: 304
As you can see here, no. of unique notes is 304. Now, let us see the distribution of the notes.
Output:

From the above plot, we can infer that most of the notes have a very low frequency. So, let us keep the top frequent notes and ignore the low-frequency ones. Here, I am defining the threshold as 50. Nevertheless, the parameter can be changed.
frequent_notes = [note_ for note_, count in freq.items() if count>=50] print(len(frequent_notes))
Output: 167
As you can see here, no. of frequently occurring notes is around 170. Now, let us prepare new musical files which contain only the top frequent notes
Preparing Data:
Preparing the input and output sequences as mentioned in the article:
Now, we will assign a unique integer to every note:
unique_x = list(set(x.ravel())) x_note_to_int = dict((note_, number) for number, note_ in enumerate(unique_x))
We will prepare the integer sequences for input data
Similarly, prepare the integer sequences for output data as well
unique_y = list(set(y)) y_note_to_int = dict((note_, number) for number, note_ in enumerate(unique_y)) y_seq=np.array([y_note_to_int[i] for i in y])
Let us preserve 80% of the data for training and the rest 20% for the evaluation:
from sklearn.model_selection import train_test_split x_tr, x_val, y_tr, y_val = train_test_split(x_seq,y_seq,test_size=0.2,random_state=0)
Model Building
I have defined 2 architectures here – WaveNet and LSTM. Please experiment with both the architectures to understand the importance of WaveNet architecture.
I have simplified the architecture of the WaveNet without adding residual and skip connections since the role of these layers is to improve the faster convergence (and WaveNet takes raw audio wave as input). But in our case, the input would be a set of nodes and chords since we are generating music:
Define the callback to save the best model during training:
mc=ModelCheckpoint('best_model.h5', monitor='val_loss', mode='min', save_best_only=True,verbose=1)
Let’s train the model with a batch size of 128 for 50 epochs:
history = model.fit(np.array(x_tr),np.array(y_tr),batch_size=128,epochs=50, validation_data=(np.array(x_val),np.array(y_val)),verbose=1, callbacks=[mc])
Loading the best model:
#loading best model
from keras.models import load_model
model = load_model('best_model.h5')
Its time to compose our own music now. We will follow the steps mentioned under the inference phase for the predictions.
Now, we will convert the integers back into the notes.
x_int_to_note = dict((number, note_) for number, note_ in enumerate(unique_x)) predicted_notes = [x_int_to_note[i] for i in predictions]
The final step is to convert back the predictions into a MIDI file. Let’s define the function to accomplish the task.
Converting the predictions into a musical file:
convert_to_midi(predicted_notes)
Some of the tunes composed by the model:
Awesome, right? But your learning doesn’t stop here. Just remember that we have built a baseline model. There are plenty of ways to improve the performance of the model even further:
- As the size of the training dataset is small, we can fine-tune a pre-trained model to build a robust system
- Collect as much as training data as you can since the deep learning model generalizes well on the larger datasets
End Notes
Deep Learning has a wide range of applications in our daily life. The key steps in solving any problem are understanding the problem statement, formulating it and defining the architecture to solve the problem.
I had a lot of fun (and learning) while working on this project. Music is a passion of mine and it was quite intriguing combining deep learning with that.
I am looking forward to hearing your approach to the problem in the comments section. And if you have any feedback on this article or any doubts/queries, kindly share them in the comments section below and I will get back to you.






















You are giving a sample from the dataset for generating. How it is acceptable? Give some new pattern not in the dataset. Let's see how it generates now
You can find the updated version of the code now!
Hi! How can we get a longer track, for example for 3 minutes? Do we need to change only the number of timesteps? Or is there anything else we need to tune?
What if I want to make the music longer? What I got is only about 3-5 sec.
Where can i find the created MIDI files?
Hey, I was wondering if it is possible for the neural networks to distinguish different instrument sounds beyond a piano (such as bass, drum, etc). If not, I would be interested to see different instrument pieced together from this ML method to create a pleasant sounding instrumental?
Thanks for this wonderful tutorial. Super cool!
Hi Aravind, amazing post! in the wavenet paper it mentions that it is not using any pooling layers. Also would love to learn ideas on how to take this model further! Thank you!
Hey Aravind, thanks for the post :) I can't get the code to work: Intellij throws the following error: UnicodeDecodeError: 'utf-8' codec can't decode byte 0xa9 in position 10: invalid start byte Could you help me? Thanks
I am facing the below error while reading the MIdi files. Can you please help me with this Error: UnicodeDecodeError: 'utf-8' codec can't decode byte 0xa9 in position 10: invalid start byte
Hey. Thanks for taking the time to write this. Was there any progress since the article was released? The end result doesn't sound very impressive :)
Hello. My name is Sriram. I would very much like to talk to you about a clarification on the above project. It's very much important to me. I'm stuck at a level. So, please consider this request and contact me. It would be a great pleasure. Thank you so much.
How do you increase the number of seconds the song is generated for , like for now its 7 seconds, and i wanted it to be for 1 or 2 mins. Please let me know
Sorry I cannot see the Midi sample music files (No Longer Shared on your Google Drive) nor the code, is there any Github Link for tgsi ti play with ?
Hi, This looks good. Can you share the dataset btw?
Dataset's link is expired. Would you please update it?
We aren't able to access the dataset. Could you please fix that?
Hi, i wanted to do something like this but with just all the wav files of my own music I have made over the years, and then use it to generate based on my own music I have created. Do you know of any guides on this or any adaptions to these instructions to do it with Wav (or mp3) instead of MIDI? There's probably only about 100 wavs, would that even be worth doing? Thanks Chris. And Great article anyway!