How does Artificial Neural Network (ANN) algorithm work? Simplified!
In the last article (click here), we briefly talked about the basics of ANN technique. But before using the technique, an analyst must know, how does the technique really work? Even though the detailed derivation may not be required, one should know the framework of the algorithm. This knowledge serves well for multiple purposes:
- Firstly, it helps us understand the impact of increasing / decreasing the dataset vertically or horizontally on computational time.
- Secondly, it helps us understand the situations or cases where the model fits best.
- Thirdly, it also helps us explain why certain model works better in certain environment or situations.
This article will provide you a basic understanding of Artificial Neural Network (ANN) framework. We won’t go into actual derivation, but the information provided in this article will be sufficient for you to appreciate and implement the algorithm. By the end of the article, I will also present my views on the three basic purposes of understanding any algorithm raised above.
Formulation of Neural network
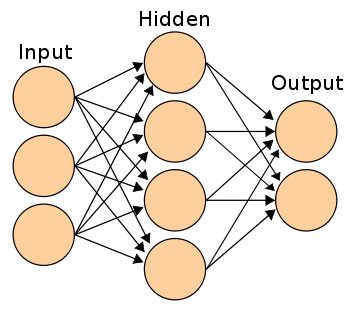
We will start with understanding formulation of a simple hidden layer neural network. A simple neural network can be represented as shown in the figure below:
The linkages between nodes are the most crucial finding in an ANN. We will get back to “how to find the weight of each linkage” after discussing the broad framework. The only known values in the above diagram are the inputs. Lets call the inputs as I1, I2 and I3, Hidden states as H1,H2.H3 and H4, Outputs as O1 and O2. The weights of the linkages can be denoted with following notation:
W(I1H1) is the weight of linkage between I1 and H1 nodes.
Following is the framework in which artificial neural networks (ANN) work:
Few statistical details about the framework
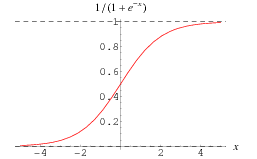
Every linkage calculation in an Artificial Neural Network (ANN) is similar. In general, we assume a sigmoid relationship between the input variables and the activation rate of hidden nodes or between the hidden nodes and the activation rate of output nodes. Let’s prepare the equation to find activation rate of H1.
Logit (H1) = W(I1H1) * I1 + W(I2H1) * I2 + W(I3H1) * I3 + Constant = f
= > P(H1) = 1/(1+e^(-f))
Following is how the sigmoid relationship looks like :
How are the weights re-calibrated? A short note
Re-calibration of weights is an easy, but a lengthy process. The only nodes where we know the error rate are the output nodes. Re-calibration of weights on the linkage between hidden node and output node is a function of this error rate on output nodes. But, how do we find the error rate at the hidden nodes? It can be statistically proved that:
Error @ H1 = W(H1O1)*Error@O1 + W(H1O2)*Error@O2
Using these errors we can re-calibrate the weights of linkage between hidden nodes and the input nodes in a similar fashion. Imagine, that this calculation is done multiple times for each of the observation in the training set.
The three basic questions
What is the correlation between the time consumed by the algorithm and the volume of data (compared to traditional models like logistic)?
As mentioned above, for each observation ANN does multiple re-calibrations for each linkage weights. Hence, the time taken by the algorithm rises much faster than other traditional algorithm for the same increase in data volume.
In what situation does the algorithm fits best?
ANN is rarely used for predictive modelling. The reason being that Artificial Neural Networks (ANN) usually tries to over-fit the relationship. ANN is generally used in cases where what has happened in past is repeated almost exactly in same way. For example, say we are playing the game of Black Jack against a computer. An intelligent opponent based on ANN would be a very good opponent in this case (assuming they can manage to keep the computation time low). With time ANN will train itself for all possible cases of card flow. And given that we are not shuffling cards with a dealer, ANN will be able to memorize every single call. Hence, it is a kind of machine learning technique which has enormous memory. But it does not work well in case where scoring population is significantly different compared to training sample. For instance, if I plan to target customer for a campaign using their past response by an ANN. I will probably be using a wrong technique as it might have over-fitted the relationship between the response and other predictors.
For same reason, it works very well in cases of image recognition and voice recognition.
What makes ANN a very strong model when it comes down to memorization?
Artificial Neural Networks (ANN) have many different coefficients, which it can optimize. Hence, it can handle much more variability as compared to traditional models.
Did you find the article useful? Have you used any other machine learning tool recently? Do you plan to use ANN in any of your business problems? If yes, share with us how you plan to go about it.










Thanks for this excellent article. I've been using ANN for a while and I understand that it can be very well used in forecasting modelling, eg. in stock market forecasting. And certainly it would over-fit in cases where the train & test data are significantly unrelated.
Its probably not a good idea to use ANN for forecasting. I have seen implementation of ANN in flood forecasting and generally speaking, it is not good specially for the cases that haven't occurred in the past. So, lets say there is a big flood which last occurred 100 years ago, and given the fact we didn't feed our model that data, there is not a remote chance that ANN can predict it. This has been very well stated in the article above.
I don't believe in the generalization power of ANNs which can memorize but can't generalize to unseen data. Does any one have examples where they do?
ANNs can do well in case of classification problems as well. I have used a very simple single layer feed forward in solving a two class commercial problem. It gives good sensitivity and specificity.
I love working with artificial neural networks algorithm. The reason being is because they are focused on replicating the reasoning patterns of the human brain. In addition, ANN's can replicate connections of neurons which work together to relay output from processed information.