How I created a package in R & published it on CRAN / GitHub (and you can too)?

Introduction

Most popular programming languages have one thing in common – they are all “Open source”. Open source is a decentralised development model which is based on community participation. The community members contribute to the development of the programming language and these contributions are publicly available to be accessed by anyone.

Community participation is the prime reason for continuous development and innovation in these open source languages like R, C++, C#, Java, PHP, Python, Ruby, etc. For data science, R is one of the most popular language. The main reason for its popularity is continuous contribution and support from R practitioners in the data science community. These packages form the backbone of R programming language.

While a lot of tutorials are being shared across on solving problems using R, the open source development gets lesser attention.  For me, creating a package and giving it back to the community meant a huge thing. It was my way to starting to give back and I know this is just the start.

In order to help expand the community further, I decided to write an article about the process of package creation and how to contribute a package to open source R community. Also, we are going to create a package and contribute it to the open source community.

Read on!

Table of Contents

1. What is a R package?
2. Why I created my first R Package?
3. Advantages and challenges of creating a package
4. Prerequisites
5. Writing you first package from scratch
6. Publishing a package
7. My experience after CRAN contribution
8. Additional tips
9. Additional resources

1. What is a R package?

A package in R is simply a reusable R function(s) with standard and self-explanatory documentation on how to use it. Sometimes, packages come with sample data as well.

There are 10,000+ packages on CRAN until today and majority of these packages have dependency on some other R package(s). This signifies that most of the packages are built over the functionality of some other package(s).

For example, a package I authored named ensembleR has main dependency on caret package along with some other packages: e1071, ipred, knitr, rmarkdown which are used for running the examples and creating vignettes.

You can realise the importance of packages in R by this handy infographic with the most commonly used libraries in R:

2. Why I created my first R Package?

Sometime back in one of the competition on Analytics Vidhya, I was trying to ensemble varioud models. I realized that there is no easy to use open source package for ensembling in R.

That’s when I decided to take this opportunity to create a simple package that will enable people to perform ensembling (stacking) using a few lines of code. Hence, I have created a package named ensembleR, which can be accessed on CRAN. This package enables people to create ensemble of several models in R. To know more about ensembling in R, read here.

This package can create millions of unique ensembles (Stacked models) and give predictions using all of them within a single line of code. The current version on CRAN is the initial release of the package. You can find more details on how this package works here.

The process of creating a package in R is both challenging as well as exciting, especially for the first time. I started off with learning the basic structure and process of creating a package.

Once I coded the package, I learnt how to submit it on CRAN to make it available to other community members. Getting it on CRAN was the toughest part because of extensive and rigorous testing of the package, which is also responsible for maintaining the quality and consistency of packages that go on CRAN.

In this article, I’ll take you through the complete process of creating a package from scratch and getting it on CRAN and/ or GitHub to be made available publicly.

3. Advantages and Challenges in creating a R package

The advantages for creating a R package are:

• Implementing new and unexplored ideas.
• Ability to help other programmers with useful functions.
• Recognition in the community.
• Contributing to the continuously evolving open source community.
• Adding value to your CV.

Also, there are certain challenges also in creating a package:

• Continuously resolving the bugs that users might report and maintenance work.
• Passing rigorous quality checks to submit them on central repositories like CRAN.
• Continuously rolling out new updates. If the maintainer of a package is not active on rolling out updates on CRAN, then the package is orphaned.

4. Pre-requisites

Before, beginning to write a package, there are few prerequisites you should be familiar with. These prerequisites are:

• Familiarity with basic R programming.
• Basic understanding of functions and looping in R.
• Working knowledge of GitHub.
• Also, you’ll need to make sure that you have installed a few packages namely: quantmod, xts, roxygen2 and devtools.

5. Writing your first package from scratch

Now let’s get started with creating a simple package of our own. Within this package, we’ll create a function to offer the functionality of predicting the stock price movement for tomorrow using simple logistic regression given the stock symbol. Simple enough. Let’s begin!

1. Create a new project by going to File > New Project.

2. You can choose an existing directory or choose to create a new one. Then choose the project type as R package.

3. This is the time you choose an appropriate name for your package. I’m going to name it StockPredictoR. For naming your packages, you can use periods (like predictoR ) or camel case as we are using here. I’ll advice you to not use underscores while naming your packages. Also, choose the appropriate subdirectory that you want to store this project in.

4. This will create the following files in the directory. All the code will be stored in R folder while the manual and supporting documents will be stored in main folder.

5. Open the DESCRIPTION file within R studio and edit the contents to best match your package description. Then save it. For this package, this is what I did.

6. If your package uses functions from some other package, then you should also include another field named Imports. Like for this package, I’m going to use functions from quantmod, stats and xts packages. There are two more fields: Depends and Suggest.When you use Imports and Depends, you mention that the user must have these packages installed for your package to work smoothly. The only difference between Imports and Depends is that Depends loads and attach the package functions, while Import only loads the package functions. You should almost always use Imports to avoid any function name masking issues.Suggests involves the library which might be required for running the examples or generating documentation. The final description file for this package looks like this

7. Go into the R folder and you’ll find hello.R script already present there. Open the hello.R script.

8. Now, you need to replace the contents of hello.R with:

#' @title
#'
#' @description
#'
#' @param
#'
#' @return
#'
#' @examples
#'
#' @export

Here,

• The ‘title’ field will contain the title of the package.
• The ‘description field is for detailed explanation of what the package does.
• The ‘param’ field will contain the parameters that we’ll take in the functions offered by the package. If there are multiple parameters, you can use multiple ‘param’ fields to specify each one separately.
• In the ‘return’ field you will mention the object that will be returned from your function.
• The ‘examples’ field will contain the demonstration examples of the function(s) that you offer in your package.
• The ‘export’ field will contain the function names that you want the end user to access. You can also hide certain functions from your code that you don’t want to offer by not mentioning them here.

9. I have gone on to fill all these fields as:

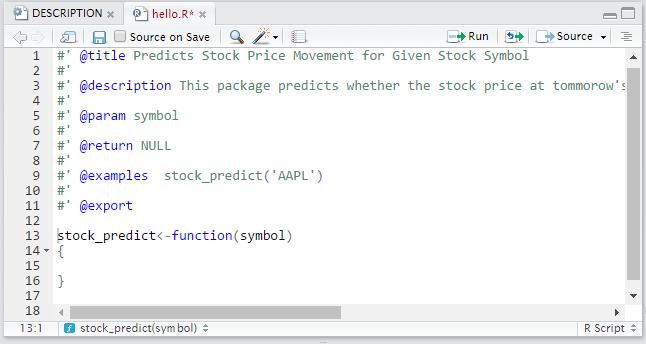
10. Now it’s time to write the function that will actually predict the stock price movement given the stock symbol. This function ‘stock_predict’ has to be written in the hello.R file itself under the export field. This is the what the hello.R file looks like after writing the function:

#' @title Predicts Stock Price Movement for Given Stock Symbol
#'
#' @description This package predicts whether the stock price at tommorow's market close would be higher or lower compared to today's closing place.
#'
#' @param symbol
#'
#' @return NULL
#'
#' @examples  stock_predict('AAPL')
#'
#' @export stock_predict
stock_predict<-function(symbol)
{

#To ignore the warnings during usage
options(warn=-1)
options("getSymbols.warning4.0"=FALSE)
#Importing price data for the given symbol
data<-data.frame(xts::as.xts(get(quantmod::getSymbols(symbol))))

#Assighning the column names
colnames(data) <- c("data.Open","data.High","data.Low","data.Close","data.Volume","data.Adjusted")

#Creating lag and lead features of price column.
data <- xts::xts(data,order.by=as.Date(rownames(data)))
data <- as.data.frame(merge(data, lm1=stats::lag(data[,'data.Adjusted'],c(-1,1,3,5,10))))

#Extracting features from Date
data$Date<-as.Date(rownames(data))
data$Day_of_month<-as.integer(format(as.Date(data$Date),"%d"))
data$Month_of_year<-as.integer(format(as.Date(data$Date),"%m"))
data$Year<-as.integer(format(as.Date(data$Date),"%y"))
data$Day_of_week<-as.factor(weekdays(data$Date))

#Naming variables for reference
today <- 'data.Adjusted'
tommorow <- 'data.Adjusted.5'

#Creating outcome
data$up_down <- as.factor(ifelse(data[,tommorow] > data[,today], 1, 0))

#Creating train and test sets
train<-data[stats::complete.cases(data),]
test<-data[nrow(data),]

#Training model
model<-stats::glm(up_down~data.Open+data.High+data.Low+data.Close+
data.Volume+data.Adjusted+data.Adjusted.1+
data.Adjusted.2+data.Adjusted.3+data.Adjusted.4+
Day_of_month+Month_of_year+Year+Day_of_week,
family=binomial(link='logit'),data=train)

#Making Predictions
pred<-as.numeric(stats::predict(model,test[,c('data.Open','data.High','data.Low','data.Close','data.Volume','data.Adjusted','data.Adjusted.1','data.Adjusted.2','data.Adjusted.3','data.Adjusted.4','Day_of_month','Month_of_year','Year','Day_of_week')],type = 'response'))

#Printing results
print("Probability of Stock price going up tommorow:")
print(pred)
}

11. Great! You have almost written your first package. Now, to make sure that your testing module is properly set up to simulate CRAN checks, go to Build > Configure Build Tools.

Now check the “Generate documentation with Roxygen” option and put “–as-cran” under Check Package space to simulate the CRAN package checking and testing.

12. Before moving forward, I’ll suggest you to go to the R folder and rename hello.R to StockPredictoR.R

13. Open the name space file and make sure that it says: export(stock_predict). If yours is different, then you should make it similar to this one:

14. We are done now. You just need to go into Build > Clean and Rebuild. Clicking on this will build the package and load it in the current environment.

15. Let’s try the example we specified and see what is the probability that the tomorrow’s closing price for the Apple stock will be higher than today’s closing price.

16. Let’s now use the package that we just created for finding the probability that the Google’s stock price at tomorrow’s close will be greater than today’s closing price.

6. Publishing a package

As you have successfully created a package in R, you’ll like to share it with others to let them use the functions in your package. For the process of publishing a package, there are two popular platforms: CRAN and GitHub.

6.1 Publishing your package on CRAN

Getting your package on CRAN is a difficult task due to the extensive and rigorous testing carried out on the packages before they can be published on CRAN. Along with passing these tests, you need to have comprehensive vignettes describing the working of your package. These vignettes will be stored in vignettes folder that you can create in the main project directory.

Once you’re sure that your package is doing well against the local simulation tests and is well documented, you need to create the source package by going to Build > Build Source Package.

After the source package is created, you can then submit an application to publish it on CRAN here.

6.2 Publishing your package on GitHub

Generally, a much easier way to make your package public is to publish it on GitHub. The simplest way to publish your package on GitHub is to create a new repository and upload the contents of the main folder (StockPredictor in our case) to that repository. I have done the same here.

Now, anyone can install and use this package using the following command:

devtools::install_github(“sauravkaushik8/SamplePackage”)

7. My experience after CRAN contribution

I can’t express how I feel after putting a package on CRAN. The usability of the package probably means very little to the outside world, but that is irrelevant. For me, I know that I have started the journey to make my favourite tool even stronger.

After making the CRAN contribution, I have realised that it has helped me in number of ways:

• I developed a deep appreciation of the kind of efforts that go in quality checks before a package gets uploaded on CRAN.
• Creating this package and submitting it on CRAN helped me gain recognition in R community especially from the people who were using my package.
• It added a lot of value to my CV and if you’re looking to boost your CV as well, I’ll highly recommend you to make open source contributions.
• This package has helped me to perform well in several data science competitions so far and I hope it would have helped several other community members as well.

8. Additional tips

Hopefully, you would have found this article helpful in creating your first open source package in R. Based on my experience, I’ll like to make a few useful suggestions:

• If you want to create your own package in R, you should convince yourself on three things:
  • What is the value addition that it makes to the global R community?
  • There is no other package already out there doing similar tasks?
  • Even if there is another package, then is my package still able to add a new functionality or make the same functionalities faster.
• For creating your own package in R, I’ll advice you to start with the steps listed above. Once, you are comfortable with the flow, you can easily get more sophisticated in function writing and learn from the codes of various packages already on GitHub.
• If you get your package on CRAN, then you need to make sure that you constantly roll out updates of your package to fix some bugs and/or add new functionality. Packages not updated for a specific period of time are orphaned by CRAN.

9. Additional Resources

• R Packages by Hadley Wickham
• Creating R packages by CRAN
• Writing R extensions

End Notes

I believe this article would have given you a good understanding of the process involved in creating your own packages in R from scratch. By following this tutorial, by now you would have hand-ons experience in creating a package in R.

Packages form the backbone of R programming language and I’ll highly encourage you to contribute to the development of the R language as well.

Did you enjoy reading this article?  Do share your views in the comment section below. If you have any doubts / questions feel free to drop them in the comments below.

Learn, compete, hack and get hired

saurav kaushik

Saurav is a Data Science enthusiast, currently in the final year of his graduation at MAIT, New Delhi. He loves to use machine learning and analytics to solve complex data problems.