Deep Learning 101: Beginners Guide to Neural Network

Introduction

If there is one area in data science that has led to the growth of Machine Learning and Artificial Intelligence in the last few years, it is Deep Learning. From research labs in universities with low success in the industry to powering every smart device on the planet – Deep Learning and Neural Networks have started a revolution.

Note: If you are more interested in learning concepts in an Audio-Visual format, We have this entire article explained in the video below. If not, you may continue reading.

In this article, we will be introducing you to the components of neural networks.

Building Blocks of a Neural Network: Layers and Neurons

There are two building blocks of a Neural Network, let’s look at each one of them in detail-

1. What are Layers in a Neural Network?

A neural network is made up of vertically stacked components called Layers. Each dotted line in the image represents a layer. There are three types of layers in a NN-

Input Layer– First is the input layer. This layer will accept the data and pass it to the rest of the network.

Hidden Layer– The second type of layer is called the hidden layer. Hidden layers are either one or more in number for a neural network. In the above case, the number is 1. Hidden layers are the ones that are actually responsible for the excellent performance and complexity of neural networks. They perform multiple functions at the same time such as data transformation, automatic feature creation, etc.

Output layer– The last type of layer is the output layer. The output layer holds the result or the output of the problem. Raw images get passed to the input layer and we receive output in the output layer. For example-

In this case, we are providing an image of a vehicle and this output layer will provide an output whether it is an emergency or non-emergency vehicle, after passing through the input and hidden layers of course.

Now, that we know about layers and their function let’s talk in detail about what each of these layers is made up of.

2. What are Neurons in a Neural Network?

A layer consists of small individual units called neurons.  A neuron in a neural network can be better understood with the help of biological neurons. An artificial neuron is similar to a biological neuron. It receives input from the other neurons, performs some processing, and produces an output.

Now let’s see an artificial neuron-

Here, X1 and X2 are inputs to the artificial neurons, f(X) represents the processing done on the inputs and y represents the output of the neuron.

What is a Firing of a neuron?

In real life, we all have heard the phrase- “Fire up those neurons” in one form or another. The same applies to artificial neurons as well. Every neuron has a tendency to fire but only in certain conditions. For example-

If we represent this f(X) by addition then this neuron may fire when the sum is greater than, say 100. While there may be a case where the other neuron may fire when the sum is greater than 10-

These certain conditions which differ neuron to neuron are called Threshold. For example, if the input X1 into the first neuron is 30 and X2 is 0:

This neuron will not fire, since the sum 30+0 = 30 is not greater than the threshold i.e 100. Whereas if the input had remained the same for the other neuron then this neuron would have fired since the sum of 30 is greater than the threshold of 10.

Now, the negative threshold is called the Bias of a neuron. Let us represent this a bit mathematically. So we can represent the firing and non-firing condition of a neuron using these couple of equations-

If the sum of the inputs is greater than the threshold then the neuron will fire. Otherwise, the neuron will not fire. Let’s simplify this equation a bit and bring the threshold to the left side of the equations. Now, this negative threshold is called Bias-

One thing to note is that in an artificial neural network, all the neurons in a layer have the same bias. Now that we have a good understanding of bias and how it represents the condition for a neuron to fire, let’s move to another aspect of an artificial neuron called Weights.

So far even in our calculation, we have assigned equal importance to all the inputs. For example-

Here X1 has a weight of 1 and  X2 has a weight of 1 and the bias has a weight of 1 but what if we want to have different weights attached to different inputs?

Let’s have a look at an example to understand this better. Suppose today is a college party and you have to decide whether you should go to the party or not based on some input conditions such as Is the weather good? Is the venue near?  Is your crush coming?

So, if the weather is good then it will be presented with a value of 1, otherwise 0. Similarly, if the venue is near it will be represented by 1, otherwise 0. And similarly for whether your crush is coming to the party or not.

Now suppose being a college teenager, you absolutely adore your crush and you can go to any lengths to see him or her. So you will definitely go to the party no matter how the weather is or how far the venue is, then you will want to assign more weight to X3 which represents the crush in comparison to the other two inputs.

Such a situation can be represented if we assign weights to an input such as this-

We can assign a weight of 3 to the weather, a weight of 2 to the venue, and a weight of 6 to the crush. Now if the sum of all these three factors that is weather, venue, and crush is greater than a threshold of 5, then you can decide to go to the party otherwise not.

Note: X0 is the bias value

So for example, we have taken initially the condition where crush is more important than the weather or the venue itself.

So let’s say for example, as we represented here the weather(X1) is bad represented by 0 and the venue(X2) is far off represented by 0 but your crush(X3) is coming to the party which is represented by 1, so when you calculate the sum after multiplying the values of Xs with their respective weights, we get a sum of 0 for Weather(X1), 0 for Venue(X2) and 6 for Crush(X3). Since 6 is greater than the threshold of 5, you will decide to go to the party. Hence the output(y) is 1.

Let’s imagine a different scenario now. Imagine you’re sick today and no matter what you will not attend the party then this situation can be represented by assigning equal weight to weather, venue, and crush with the threshold of 4.

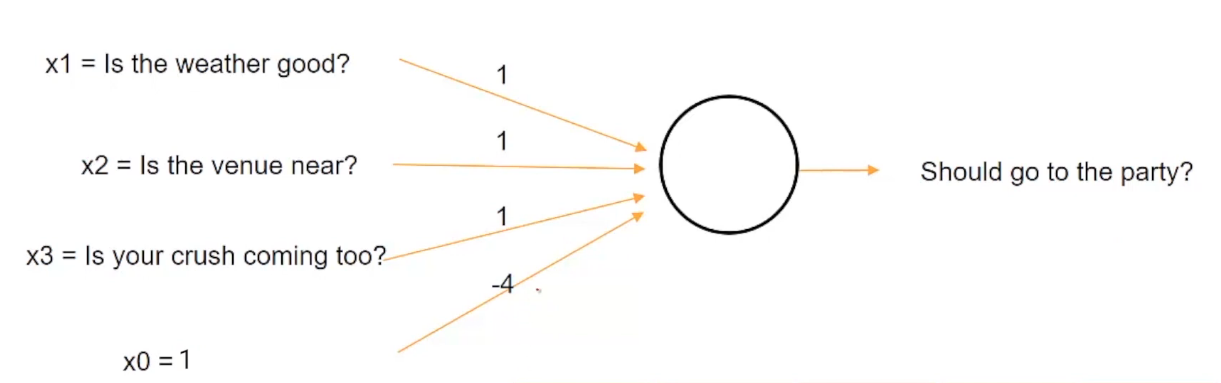
Now, in this case we are changing the value of the threshold and setting it to a value of 4 so even if the weather is good, the venue is near and your crush is coming, you won’t be going to the party since the sum i.e 1 + 1 + 1 equal to 3, is less than the threshold value of 4.

This w0, w1, w2, and w3 are called the weights of neurons and are different for different neurons. These weights are the ones that a neural network has to learn to make good decisions.

Activation Functions in a Neural Network

Now that we know how a neural network combines different inputs using weights, let’s move to the last aspect of a neuron called the Activation functions. So far what we have been doing is simply adding some weighted inputs and calculating some output and this output can read from minus infinity to infinity.

But this can be challenged in many circumstances. Assume we first want to estimate the age of a person from his height, weight, and cholesterol level and then classify the person as old or not, based on if the age is greater than 60.

Now if we use this given neuron then the age of -20 is even possible. You know that the range of age according to the current structure of this neuron will range from -∞ to ∞. So even the age of someone as -20 is possible, given this absurd range for age we can still use our condition to decide whether a person is old or not. For example, if we have said a certain criterion such as a person is old only if the age is greater than 60. So even if the age comes out to be -20 we can use this criterion to classify the person as not old.

But it would have been much better had the age made much more sense such as if the output of this neuron which represents the age had been in the range of let’s say 0 to 120. So, how can we solve this problem when the output of a neuron is not in a particular range?

One method is to clip the age on the negative side would be to use a function such as max(0, X).

Now let’s first note the original condition, before using any function. For the positive X, we had a positive Y, and for negative X we had a negative Y. Here x-axis represents the actual values and y represents the transformed values-

But now if you want to get rid of the negative values what we can do is use a function like max(0, X). Using this function anything which is on the negative side of the x-axis gets clipped to 0.

This type of function is called a ReLU function and these classes of functions, which transform the combined input are called Activation functions. So, ReLU is an activation function.

Depending on the type of transformation needed there can be different kinds of activation functions. Let’s have a look at some of the popular activation functions-

1. Sigmoid activation function– This function transforms the range of combined inputs to a range between 0 and 1. For example, if the output is from minus infinity to infinity which is represented by the x-axis, the sigmoid function will restrict this infinite range to a value between 0 & 1.
2. Tanh activation function- This function transforms the range of combined inputs to a range between -1 and 1. Tanh looks very similar to the shape of the sigmoid but it restricts the range between -1 and 1.

Different activation functions perform differently on different data distribution. So sometimes you have to try and check different activation functions and find out which works better for a particular problem.

Frequently Asked Questions

End Notes

So far, we have discussed that the neural network is composed of different types of layers stacked together and each of these layers is composed of individual units called Neurons. Every neuron has three properties: first is biased, second is weight and third is the activation function.

Further, bias is the negative threshold after which you want the neuron to fire. Weight is how you define which input is more important to the others. The activation function helps to transform the combined weighted input to arrange according to the need at hand.

I highly recommend you check out our Certified AI & ML BlackBelt Plus Program to begin your journey into the fascinating world of data science and learn these and many more topics.

I hope this article works as a starting point to your learning towards neural networks and deep learning.

Reach out to us in the comments below in case you have any doubts.

Himanshi Singh 27 Jul 2023

I am a data lover and I love to extract and understand the hidden patterns in the data. I want to learn and grow in the field of Machine Learning and Data Science.