Introduction
Handwritten digit classification is one of the multiclass classification problem statements. In this article, we’ll introduce the multiclass classification using Support Vector Machines (SVM). We’ll first see what exactly is meant by multiclass classification, and we’ll discuss how SVM is applied for the multiclass classification problem. Finally, we’ll look at Python code for multiclass classification using Sklearn SVM.
The particular question on which we will be focusing in this article is as follows:
“How can you extend a binary classifier to a multi-class classifier in case of SVM algorithm?”
Multiclass Classification: In this type of classification, the machine learning model should classify an instance as only one of three classes or more. For Example, Classifying a text as positive, negative, or neutral.
Learning Objectives
- Understand the concept of multiclass classification and its significance in solving complex classification problems.
- Explore the fundamentals of Support Vector Machines (SVM) and their role in multiclass classification tasks.
- Identify and compare three popular approaches for multiclass classification using SVM: One vs One (OVO), One vs All (OVA), and Directed Acyclic Graph (DAG).
- Gain insights into the working principles of each approach, including their advantages, challenges, and implementation strategies.
- Recognize key aspects such as regularization, kernel functions, and optimization techniques, and their impact on multiclass SVM performance.
This article was published as a part of the Data Science Blogathon.
Table of contents
What are Support Vector Machines (SVM)?
SVM is a supervised machine learning algorithm that helps in both classification and regression problem statements. It tries to find an optimal boundary (known as hyperplane) between different classes. In simple words, SVM does complex data transformations depending on the selected kernel function, and based on those transformations, it aims to maximize the separation boundaries between your data points.
- Working of SVM: In the simplest form where there is a linear separation, SVM tries to find a line that maximizes the separation between a two-class data set of 2-dimensional space points.
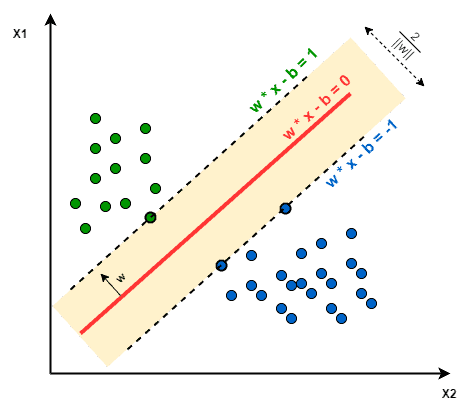
- The objective of SVM: The objective of SVM is to find a hyperplane that maximizes the separation of the data points to their actual classes in an n-dimensional space. The data points which are at the minimum distance to the hyperplane i.e, closest points are called Support Vectors.
For example: In the given diagram, the support vectors consist of three points layered on the scattered lines, comprising 2 blue and 1 green support vectors, with the separation hyperplane represented by the solid red line.
Multiclass Classification Using SVM
In its most basic type, SVM doesn’t support multiclass classification. For multiclass classification, the same principle is utilized after breaking down the multi-classification problem into smaller subproblems, all of which are binary classification problems.
The popular methods that are used to perform multi-classification on the problem statements using SVM (multiclass support vector machines) are as follows:
- One vs One (OVO) approach
- Directed Acyclic Graph (DAG) approach
- One vs All (OVA) approach
Now, let’s discuss each of these approaches one by one in a detailed manner:
One vs One (OVO)
This method decomposes our multiclass classification problem into binary subproblems. Consequently, we obtain binary classifiers for each pair of classes. To make final predictions, we employ majority voting along with the distance from the margin as a confidence criterion.
However, a significant drawback of this approach is the necessity to train numerous SVMs.
In the case of multi-class/multi-label problems with L categories, consider the (s, t)-th classifier:
- Positive Samples: all points in class s ({ xi: s ∈ yi })
- Negative samples: all points in class t ({ xi: t ∈ yi })
- fs, t(x): decision value of this classifier (where a large value of fs, t(x) indicates a higher probability for label s over label t)
- f t, s(x) = – f s, t(x)
- Prediction: f(x) = argmax s ( Σ t fs, t(x) )
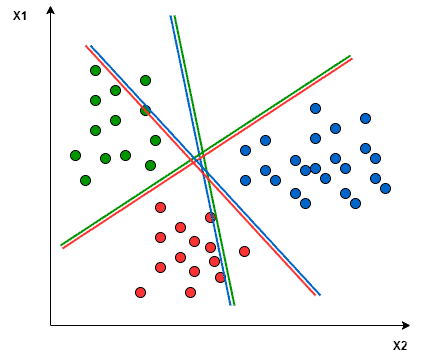
For instance, let’s consider a scenario with three class classification problems: Green, Red, and Blue.

In the One-to-One approach, we aim to identify the hyperplane that separates every pair of classes, disregarding the points of the third class. For example, the Red-Blue line maximizes separation only between blue and red points, without considering the green points.
Also Read: Top 10 Machine Learning Algorithms to Use in 2024
One vs All (OVA)
In this technique, for an N class problem, we train N SVMs:
SVM number -1 learns “class_output = 1” vs “class_output ≠ 1” SVM number -2 learns “class_output = 2” vs “class_output ≠ 2” . . . . SVM number -N learns “class_output = N” vs “class_output ≠ N”
To predict the output for new input data, we predict with each of the built SVMs and then determine which one yields the prediction farthest into the positive region, acting as a confidence criterion for a specific SVM.
Challenges in N SVMs
However, there are challenges in training these N SVMs:
- High Computation: Implementing the One vs All (OVA) strategy requires more training points, leading to increased computation.
- Imbalanced Problems: For instance, in an MNIST dataset with 10 classes (0 to 9) and 1000 points per class, one SVM may have 9000 points while another has only 1000, resulting in an unbalanced problem.
To address this issue:
- Utilize the 3-sigma rule of the normal distribution to fit data and subsample accordingly, maintaining class distribution.
- Randomly select data points from the majority class.
- Employ popular subsampling techniques like SMOTE.
For multi-class/multi-label problems with L categories:
For the t-th classifier:
- Positive Samples: all points in class t ({ xi: t ∈ yi })
- Negative samples: all points not in class t ({ xi: t ∉ yi })
- ft(x): the decision value for the t-th classifier (where a large value of ft indicates a higher probability that x is in class t)
- Prediction: f(x) = argmax t ft(x)
In the One vs All approach, a hyperplane is sought to separate the classes, considering all points and dividing them into two groups: one for the points of the class being analyzed and another for all other points.
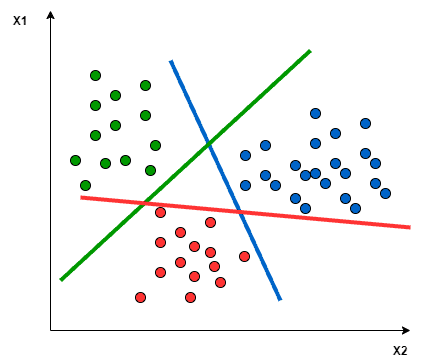
A single SVM conducts binary classification and can differentiate between two classes. Accordingly:
- In the One vs All approach, the classifier employs L SVMs.
- In the One vs One approach, the classifier uses L(L-1)/2 SVMs.
Directed Acyclic Graph (DAG)
This approach is more hierarchical and aims to address the shortcomings of the One vs One and One vs All approach.
It adopts a graphical approach wherein classes are grouped based on logical categorization.
Benefits: This method offers advantages such as fewer SVM trains compared to the OVA approach, and it mitigates diversity issues from the majority class, which is a concern in the OVA approach.
Challenge: When the dataset doesn’t naturally come in distinct groups (e.g., CIFAR 10 image classification dataset), applying this approach directly becomes problematic. In such cases, identifying the logical grouping within the dataset becomes a manual task.
Conclusion
In conclusion, multiclass classification using Support Vector Machines (SVM) is a powerful approach for solving complex classification problems like handwritten digit recognition. SVMs extend binary classifiers to handle multiple class labels, enabling accurate classification into predefined categories.
We explored fundamental SVM concepts, including the objective of finding an optimal decision boundary and identifying support vectors. Three popular approaches for multiclass classification with SVMs were discussed: One vs One (OVO), One vs All (OVA), and Directed Acyclic Graph (DAG), each with unique advantages and challenges.
Key aspects such as regularization, kernel functions (linear, polynomial, radial basis function), and optimization techniques were highlighted, emphasizing the role of scikit-learn for implementation.
While this article covered essential concepts, advanced topics like cross-validation, decision boundaries, and model evaluation metrics remain unexplored. Additionally, topics like neural networks and non-linear SVMs offer alternative approaches to classification.
In summary, multiclass SVMs offer a robust framework for classifying data into multiple categories, making them valuable in data science and AI. By mastering these concepts, practitioners can build accurate models for various applications.
Key Takeaways
- Multiclass classification using SVM extends binary classifiers to handle multiple class labels, enabling accurate classification into predefined categories like handwritten digit recognition.
- Three main approaches for multiclass classification with SVM are One vs One (OVO), One vs All (OVA), and Directed Acyclic Graph (DAG), each with unique advantages and challenges.
- The OVO approach breaks down the multiclass problem into binary subproblems, while OVA trains separate SVM classifiers for each class. DAG offers a hierarchical grouping approach, reducing diversity from the majority class.
- Challenges in training multiple SVM classifiers include increased computation and unbalanced class distributions, which can be addressed through subsampling and techniques like SMOTE.
- While this article covers essential concepts, advanced topics like cross-validation and model evaluation metrics remain unexplored, indicating further avenues for exploration in multiclass SVM classification.
Frequently Asked Questions
A. Multiclass classification involves categorizing instances into multiple classes, such as positive, negative, or neutral sentiments in text data. SVM tackles multiclass classification by breaking it into smaller binary classification subproblems, employing techniques like one-vs-rest or one-vs-one.
A. Popular methods include one-vs-one (OVO), one-vs-all (OVA), and Directed Acyclic Graph (DAG) approaches. These methods divide the multiclass problem into binary subproblems, leveraging multiple SVM classifiers’ decision functions.
A. In the OVA approach, each class has its SVM classifier, treating samples from that class as positive examples and others as negatives. The final prediction selects the class with the highest confidence score among all SVM classifiers.
A. Training numerous SVM classifiers can pose issues like increased computation and unbalanced class distributions. Techniques like subsampling from the majority class or using SMOTE algorithms help mitigate these challenges and enhance classifier performance.
A. The DAG approach is more hierarchical and aims to overcome limitations of OVA and OVO methods. It groups classes based on logical grouping, reducing diversity in the majority class. However, it may require manual class grouping unlike other approaches.
The media shown in this article are not owned by Analytics Vidhya and is used at the Author’s discretion.








I just admire your intelligence!!!