Interview Prep
Career
GenAI
Prompt Engg
ChatGPT
LLM
Langchain
RAG
AI Agents
Machine Learning
Deep Learning
GenAI Tools
LLMOps
Python
NLP
SQL
AIML Projects

Reading list

Machine Learning Basics for a Newbie
6 Steps of Machine learning Lifecycle Introduction to Predictive Modeling
Introduction to Exploratory Data Analysis & Data Insights Descriptive Statistics Inferential Statistics How to Understand Population Distributions?
Reading Data Files into Python Different Variable Datatypes
Probability for Data Science Basic Concepts of Probability Axioms of Probability Conditional Probability
Central Tendencies for Continuous Variables Spread of Data KDE plots for Continuous Variable Overview of Distribution for Continuous variables Normal Distribution Skewed Distribution Skeweness and Kurtosis Distribution for Continuous Variable
Central Tendencies for Categorical Variables Understanding Discrete Distributions Performing EDA on Categorical Variables
Dealing with Missing Values Understanding Outliers Identifying Outliers in Data Outlier Detection in Python Outliers Detection Using IQR, Z-score, LOF and DBSCAN
Sample and Population Central Limit Theorem Confidence Interval and Margin of Error
Bivariate Analysis Introduction
Covariance Pearson Correlation Spearman's Correlation & Kendall's Tau Correlation versus Causation Tabular and Graphical methods for Bivariate Analysis Performing Bivariate Analysis on Continuous-Continuous Variables
Tabular and Graphical methods for Continuous-Categorical Variables Introduction to Hypothesis Testing P-value Two sample Z-test T-test T-test vs Z-test Performing Bivariate Analysis on Continuous-Catagorical variables
Chi-Squares Test Bivariate Analysis on Categorical Categorical Variables
Multivariate Analysis A Comprehensive Guide to Data Exploration The Data Science behind IPL
Supervised Learning vs Unsupervised Learning Reinforcement Learning Generative and Descriminative Models Parametric and Non Parametric model
Machine Learning Pipeline Preparing Dataset Build a Benchmark Model: Regression Build a Benchmark Model: Classification
Evaluation Metrics for Machine Learning Everyone should know Confusion Matrix Accuracy Precision and Recall AUC-ROC Log Loss R2 and Adjusted R2
Dealing with Missing Values Replacing Missing Values Imputing Missing Values in Data Working with Categorical Variables Working with Outliers Preprocessing Data for Model Building
Understanding Cost Function Understanding Gradient Descent Math Behind Gradient Descent Assumptions of Linear Regression Implement Linear Regression from Scratch Train Linear Regression in Python Implementing Linear Regression in R Diagnosing Residual Plots in Linear Regression Models Generalized Linear Models Introduction to Logistic Regression Odds Ratio Implementing Logistic Regression from Scratch Introduction to Scikit-learn in Python Train Logistic Regression in python Multiclass using Logistic Regression How to use Multinomial and Ordinal Logistic Regression in R ? Challenges with Linear Regression Introduction to Regularisation Implementing Regularisation Ridge Regression Lasso Regression
Introduction to K Nearest Neighbours Determining the Right Value of K in KNN Implement KNN from Scratch Implement KNN in Python
Bias Variance Tradeoff Introduction to Overfitting and Underfitting Visualizing Overfitting and Underfitting Selecting the Right Model What is Validation? Hold-Out Validation Understanding K Fold Cross Validation
Introduction to Feature Selection Feature Selection Algorithms Missing Value Ratio Low Variance Filter High Correlation Filter Backward Feature Elimination Forward Feature Selection Implement Feature Selection in Python Implement Feature Selection in R
Introduction to Decision Tree Purity in Decision Tree Terminologies Related to Decision Tree How to Select Best Split Point in Decision Tree? Chi-Squares Information Gain Reduction in Variance Optimizing Performance of Decision Tree Train Decision Tree using Scikit Learn Pruning of Decision Trees
Introduction to Feature Engineering Feature Transformation Feature Scaling Feature Engineering Frequency Encoding Automated Feature Engineering: Feature Tools
Introduction to Naive Bayes Conditional Probability and Bayes Theorem Introduction to Bayesian Adjustment Rating: The Incredible Concept Behind Online Ratings! Working of Naive Bayes Math behind Naive Bayes Types of Naive Bayes Implementation of Naive Bayes
Understanding how to solve Multiclass and Multilabled Classification Problem Evaluation Metrics: Multi Class Classification
Introduction to Ensemble Techniques Basic Ensemble Techniques Implementing Basic Ensemble Techniques Finding Optimal Weights of Ensemble Learner using Neural Network Why Ensemble Models Work well?
Introduction to Stacking Implementing Stacking Variants of Stacking Implementing Variants of Stacking Introduction to Blending Bootstrap Sampling Introduction to Random Sampling Hyper-parameters of Random Forest Implementing Random Forest Out-of-Bag (OOB) Score in the Random Forest IPL Team Win Prediction Project Using Machine Learning Introduction to Boosting Gradient Boosting Algorithm Math behind GBM Implementing GBM in python Regularized Greedy Forests Extreme Gradient Boosting Implementing XGBM in python Tuning Hyperparameters of XGBoost in Python Implement XGBM in R/H2O Adaptive Boosting Implementing Adaptive Boosing LightGBM Implementing LightGBM in Python Catboost Implementing Catboost in Python
Different Hyperparameter Tuning methods Implementing Different Hyperparameter Tuning methods GridsearchCV RandomizedsearchCV Bayesian Optimization for Hyperparameter Tuning Hyperopt
Understanding SVM Algorithm SVM Kernels In-depth Intuition and Practical Implementation SVM Kernel Tricks Kernels and Hyperparameters in SVM Implementing SVM from Scratch in Python and R
Introduction to Principal Component Analysis Steps to Perform Principal Compound Analysis Computation of Covariance Matrix Finding Eigenvectors and Eigenvalues Implementing PCA in python Visualizing PCA A Brief Introduction to Linear Discriminant Analysis Introduction to Factor Analysis
Introduction to Clustering Applications of Clustering Evaluation Metrics for Clustering Understanding K-Means Implementation of K-Means in Python Implementation of K-Means in R Choosing Right Value for K Profiling Market Segments using K-Means Clustering Hierarchical Clustering Implementation of Hierarchial Clustering DBSCAN Defining Similarity between clusters Build Better and Accurate Clusters with Gaussian Mixture Models
Understand Basics of Recommendation Engine with Case Study
8 Ways to Improve Accuracy of Machine Learning Models
Introduction to Dask Working with CuML
Introduction to Machine Learning Interpretability Framework and Interpretable Models model Agnostic Methods for Interpretability Implementing Interpretable Model Understanding SHAP Out-of-Core ML Introduction to Interpretable Machine Learning Models Model Agnostic Methods for Interpretability Game Theory & Shapley Values
Introduction to Machine Learning Interpretability Framework and Interpretable Models model Agnostic Methods for Interpretability Implementing Interpretable Model Understanding SHAP Out-of-Core ML Introduction to Interpretable Machine Learning Models Model Agnostic Methods for Interpretability Game Theory & Shapley Values
Introduction to AutoML Implementation of MLBox Introduction to PyCaret TPOT Auto-Sklearn EvalML
Pickle and Joblib Introduction to Model Deployment
Deploying Machine Learning Model using Streamlit Deploying ML Models in Docker Deploy Using Streamlit Deploy on Heroku Deploy Using Netlify Introduction to Amazon Sagemaker Setting up Amazon SageMaker Using SageMaker Endpoint to Generate Inference Deploy on Microsoft Azure Cloud Introduction to Flask for Model Deploying ML model using Flask
Model Deployment in Android Model Deployment in Iphone

Solving Accuracy vs. Cost using probabilities (with case study)

Tavish Srivastava
Tavish Srivastava Last Updated : 18 Apr, 2015
5 min read

confusion

As a manager, you face cost vs. quality / accuracy trade-offs on a regular basis. This can be in the form of any of these questions:

  • Should we invest more time and resources to gather incremental data and take more informed decision?
  • What is the value gained by asking the analyst in your team to spend one more day on data cleansing?
  • What is the incremental gain by trying out some more hypothesis and gain slightly higher lift curve in your predictive models?
  • What is the value of extra time / resources spent on gathering additional information?

If you are a decision making authority, these dilemma arise quite often. Sadly, not many people have a framework to answer these questions. They end up taking these decision based on their gut or change their stand multiple times in the process.

If you do not put a framework around these problems, your decision making is dependent on how the problem is narrated to you or how you think about it at that instance. This also leads to change in stand / decisions multiple times. In this article, I have laid out a simple framework to answer these questions and have illustrated its usage through a case study.

[stextbox id=”section”] Framework: [/stextbox]

The framework for these situations is fairly simple. As a stand alone decision, you invest resources until the value created by these investments is higher than the cost incurred.

On the other hand, If there are multiple opportunities with limited resources, you invest in the projects, which give you the highest ROI.

[stextbox id=”section”] Case study – Background : [/stextbox]

You are the general manager of FUORD, an automobile company in India. FUORD has recently launched a model in India and China called Bistra. The engine of this model has been outsourced to two companies, namely X and Y (referred as vendor after this). Both X and Y make an identical design of the engines. However, 10 out of every 100 engines from Vendor X are faulty in working whereas 1 out of 100 engines of Y is faulty in working. India and China import exact the same number of engines. FUORD has a policy of not revealing the vendor name while sending the engines to any country. Hence, in any month India has an equal probability of receiving either engines manufactured by X or by Y.

[stextbox id=”section”] Faulty engine found :: [/stextbox]

After 10 months of launch of Bistra, you found one of the engines is of wrong design. A fault in design is against the code of conduct of FUORD and the contract with this supplier needs to be terminated immediately. But the fix is that neither you nor anyone in the firm is sure whether this engine was supplied by X or Y. Here are various costs involved in the process:

  • Test for working of each engine costs the company $40 k   .
  • Cost of a decision of terminating a wrong vendor contract is $1 MM.

Should you test an engine for its working, if it is faulty or not before terminating the supply from a vendor?

Note: Fault in design and fault in working of the engine are two independent events.

[stextbox id=”section”]The play of probabilities: [/stextbox]

What is the probability that the lot in India in the 10th month of the launch came from X? Obviously 0.5, as there are only two options of choosing a vendors and both equally likely. Can you take a decision to terminate any of the two vendors based on your intuition? Probably not. What do you do in such situations? Collect more information.

But is the collection of information worth the cost which you will incur to test an engine. Let’s try to find out the expected costs involved.

[stextbox id=”grey”]

Event X : The lot in the 10th month is from X

Event Y : The lot in the 10th month is from Y

Event F: The chosen engine is faulty

Event P: The chosen engine is perfect

P(X) = P(Y) = 0.5

P(F/X ) = Probability of the engine being faulty given that the lot is from X = 0.1 (Given)

P(F/Y ) = Probability of the engine being faulty given that the lot is from Y = 0.01 (Given)

[/stextbox]

We already know that

condition2

 

condition1

[stextbox id=”grey”]

P(F) = Probability of the engine being faulty

= P(F∩X) + P(F∩Y)

= P(F/X)*F(X) + P(F/Y)*P(Y)

= 0.5*(0.1 + 0.01) = 0.055

P(X/F) = Probability of lot being from X given that the first random engine chosen is faulty

= P(X∩F) /P(F)

= 0.5*0.1/0.055 = 0.909

P(P) = Probability of the engine being perfect  = P(P∩X) + P(P∩Y)

= P(P/X)*P(X) + P(P/Y)*P(Y)

= 0.5*(0.9 + 0.99) = 0.945

P(X/P) = Probability of lot being from X given that the first random engine chosen is perfect

= P(X∩P) /P(P)

= 0.5*0.9/0.945 = 0.47

P(Y/P) = 0.53

[/stextbox]
K : Event of choosing the correct vendor after the first engine assessment.

Good Choice Bad Choice

[stextbox id=”grey”]

P(K) = P(K∩F) + P(K∩P)

= P(F) * P(K/F) + P(P)*P(K/P)

= 0.055*0.909 + 0.945*0.53

= 0.05 +  0.5 = 0.55

Now let’s make some cost estimations.

Expected value of cost if engine assessment is not done= A = $1MM * 0.5 = $500 k

Expected value of cost if the engine assessment is done = B = $40 k + 0.45 *$1MM = $490k

[/stextbox]

Clearly A > B and, hence, assessment of first engine is totally justified. Also, on a stand alone basis, we were able to reduce cost of wrong assessment by $10 k, by investing $40 k

[stextbox id=”section”]  End Notes :  [/stextbox]

In this part of the case study, we took a very simple case with a single step of processing. Say, you completed the first test and found the engine to be perfect. Now you wish to check if the second test is cost effective or not. Make cases and find the expected cost of test and cost saved by the test. Make the comparison and write in the box below your recommendation to do the second test or not?

Did you find the article useful? Share with us how you would have approached making strategies mentioned in the article. Do let us know your thoughts about this article in the box below.

If you like what you just read & want to continue your analytics learning, subscribe to our emails, follow us on twitter or like our facebook page.

Tavish Srivastava
Tavish Srivastava

Tavish Srivastava, co-founder and Chief Strategy Officer of Analytics Vidhya, is an IIT Madras graduate and a passionate data-science professional with 8+ years of diverse experience in markets including the US, India and Singapore, domains including Digital Acquisitions, Customer Servicing and Customer Management, and industry including Retail Banking, Credit Cards and Insurance. He is fascinated by the idea of artificial intelligence inspired by human intelligence and enjoys every discussion, theory or even movie related to this idea.

Free Courses

Generative AI 4.7

Generative AI - A Way of Life

Explore Generative AI for beginners: create text and images, use top AI tools, learn practical skills, and ethics.
Large Language Models 4.5

Getting Started with Large Language Models

Master Large Language Models (LLMs) with this course, offering clear guidance in NLP and model training made simple.
Prompt Engineering 4.6

Building LLM Applications using Prompt Engineering

This free course guides you on building LLM apps, mastering prompt engineering, and developing chatbots with enterprise data.
LlamaIndex 4.8

Improving Real World RAG Systems: Key Challenges & Practical Solutions

Explore practical solutions, advanced retrieval strategies, and agentic RAG systems to improve context, relevance, and accuracy in AI-driven applications.
RAG systems using LlamaIndex 4.7

Microsoft Excel: Formulas & Functions

Master MS Excel for data analysis with key formulas, functions, and LookUp tools in this comprehensive course.

Recommended Articles

Responses From Readers

Clear

sumalatha
sumalatha

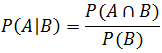
great, clarified my understanding about probability. plz keep providing this type of stuff. thank you.

123

Write for us

Write, captivate, and earn accolades and rewards for your work
  • Reach a Global Audience
  • Get Expert Feedback
  • Build Your Brand & Audience
  • Cash In on Your Knowledge
  • Join a Thriving Community
  • Level Up Your Data Science Game
imag

We use cookies essential for this site to function well. Please click to help us improve its usefulness with additional cookies. Learn about our use of cookies in our Privacy Policy & Cookies Policy.

Show details