Introduction
Encountering ensemble learning algorithm in winning solutions of data science competitions has become a norm now. The ability to train multiple learners on a set of hypothesis, not only adds robustness to the model, but also enables it to deliver highly accurate predictions. In case you missed, I would recommend reading Basics of Ensemble Learning Explained in Simple English before you go forward.
While building ensemble models, one of most common challenge that people face is to find optimal weights. Few of them fight hard to solve this challenge and the not so brave ones, convince themselves to apply simple bagging, which assumes equal weight for all models and takes the average of all predicted values.
It often works well because it removes variance error from individual models. However, as we know, assigning equal weights is not the best approach to obtain the best combination of models. What could be an alternate way? In this article, I’ve solved the problem of finding out the optimal weights in ensemble learners using neural network in R Programming.
Let’s consider a simple problem
Imagine you have built 3 models on a given (hypothetical) data set. Each of these models predicts probability of output for an event.
In the following figure : Model 1, Model 2 and Model 3 are the three predictive models. Each of them have their own uniqueness and can work as a team to perform even better than individually best model.
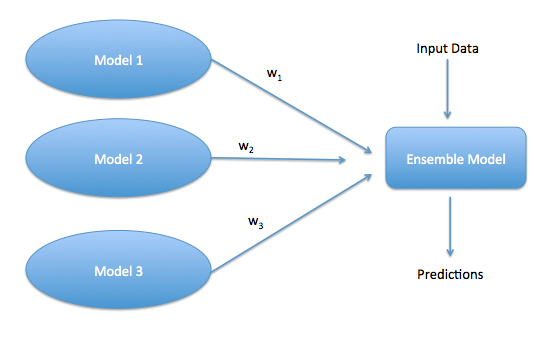 We initially assume a 33.33% weight for each of the model and build an Ensemble model. Here, the challenge is to optimize these weights w1, w2 and w3 in such a fashion as to build a highly powerful ensemble model.
We initially assume a 33.33% weight for each of the model and build an Ensemble model. Here, the challenge is to optimize these weights w1, w2 and w3 in such a fashion as to build a highly powerful ensemble model.
What could be a traditional approach to this problem?
Assume p1 , p2 and p3 are three outputs from the three models respectively. We need to optimize w1, w2 and w3 to optimize an objective function. Let’s try to write down the constraints and objective function mathematically :
Constraint :
w1 + w2 + w3 = 1
p = w1 * p1 + w2 * p2 + w3 * p3
Objective function (Maximize Likelihood function) :
Maximize (Product over all observations [ (p) ^ (y) * (1-p) ^ (1-y) ] )
where y is the response flag for the observation p is the predicted probability through ensemble model p1, p2 and p3 : predicted probabilities from individual model w1, w2 and w3 : weights given to each model
This is a classic case of simplex optimization. However, with a huge number of models to bag, and diving into mathematical formulas every time can be stressful and time consuming at times. Hence, we need a smarter method here.
We’ll now learn to find these weights without getting into such mathematical formulation using neural network implementation.
How to find optimal weights using Neural Network?
I understand, neural network implementation can be quite overwhelming at times. Hence, to solve the current case in hand, we’ll not deep dive into the complex concepts of deep neural network.
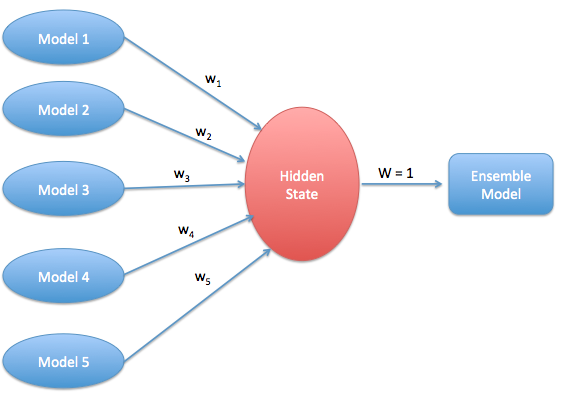
Basically, neural network operates on finding weights for interlink between ( input variable to hidden node) and ( hidden node to output node). Our objective here is to find the right combination of weights from input nodes directly to the output node.
Here is an easy and diligent way to accomplish this task. We restrict the number of hidden nodes to one. This will automatically adjust the weight from hidden node to output node as 1. This implies that the hidden node and the output node is no longer different.
Here is a simplistic schema to represent what we just discussed :
So we found a way! This will automatically accomplish what we were trying to do using simplex equations. Let’s put this formulation down to a R code
# x is a matrix of multiple predictions coming from different learners #y is a vector of all output flags #x_test is a matrix of multiple predictions on an unseen sample x <- as.matrix(prediction_table) y <- as.numeric(output_flags) nn <- dbn.dnn.train(x,y,hidden = c(1), activationfun = "sigm",learningrate = 0.2,momentum = 0.8) nn_predict <- n.predict(nn,x) nn_predict_test <- n.predict(nn,x_test)
End Notes
I have implemented this logic on multiple Kaggle problems and found that the results are quite encouraging. Here is one such example from a recent competition:
- Simple logistic model at score of 100
- Best machine learning model at score of 107
- Simple bagging techniques of 110, and finally
- Optimized weights using neural network of 113.
In this article, I’ve explained the method to find optimal weight in an ensemble model using a traditional approach and neural network implementation (recommended).









Hi Tavish, I found this article very interesting. However I need some more understanding on the matrices x,y and x_test used in your code. For example I have 3 models and their corresponding predicted values in the following format: Actual Value | Predicted Value by Model1 | Predicted Value by Model2 | Predicted Value by Model3 A | A1 | A2 | A3 B | B1 | B2 | B3 C | C1 | C2 | C3 - - - In such a case what will be the contents of x,y and test_x?
Hi Samrat, In this case x will be A1,A2,A3 and y will be column A. To build test you need an unseen population. Hope this clarifies. Tavish
Hi Tavish, Excellent Write-up. i have a Quick question. How to set activation function for Numerical Predicted values( it might be Time Series or Regression Output). i had tried "linear" and "tanh" also. but i 'm getting only Categorical Output. like 1 or 0. Please help me this out
Hi Karthi, If you are using neural net package, then using the code mentioned in the article will give you probability prediction.
Thanks for the explanation Tavish. I'm not familiar with the R package. " nn <- dbn.dnn.train(x,y,hidden = c(1), activationfun = "sigm",learningrate = 0.2,momentum = 0.8) " According to the code above, the activiationfun is "sigm" for both hidden node and output node. And the weight W from hidden node to output node is fixed to 1 , which means W will not be updated during the backpropagation. Am I right ? or the network setting is not like this?
Thanks lot Tavish.
Trying to implement this logic for my model. Iam not able to find weights w1,w2,w3,... for the model in dbn.dnn.train. I understand number of weights should be the same as number of columns of predictions given by different models. Searching documentation of dbn.dnn.train doesnt give "Values" description which is normally given in other packages. Please give a pointer on this.