Introduction
Statistics is one of the key ingredient any data scientist must know to have a long successful career in data science industry. After the overwhelming response from Skilltest Statistics we immediately launched Skilltest Statistics II. We launched this unique self-assessment challenge for individuals to test their knowledge and identify their strengths & weaknesses.
As we had promised the Skilltest Statistics II will be more advanced, we delivered some nerve wrenching questions. The heat during the competition was intense and we kept wondering who will make it to the top this time.
More than 1100 participants registered for the challenge and we received around 401 submissions. A loud applaud to all the participants for making it a big success and heartiest congratulations to the winners.
Overall Results
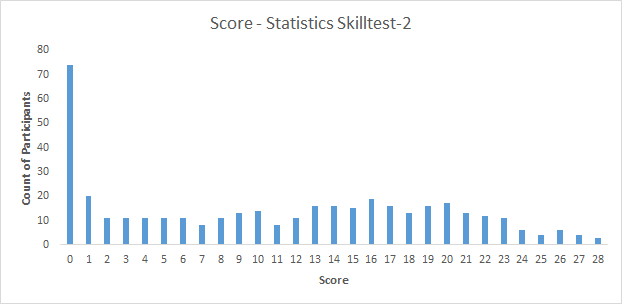
Who could have asked for a better way to analyze the results of a statistical skill test on this topic? Here is the distribution of the scores:
Here are a few measures of the distribution:
Mean = 10.86
Median = 11.00
Let us look at the variance:
Standard Deviation = 8.35
95% confidence interval – [0, 27.23)
So, congratulations for the top 3 people (27 and above) to set themselves above the rest of the population.
If your score is more than 18, you are in the top 25 percentile – you deserve a pat!
Skilltest Questions and Answers
The skill test consisted of 40 questions based on hypothesis testing, t-test and correlation. We think any data scientist should know these concepts like back of their hand.
Read on to find out detailed explaination of each question.
1) Numerous studies have demonstrated that listening to music while studying can improve memory. To demonstrate this phenomenon a researcher obtains a sample of 36 students and gives them a standardised memory test while they listen to music. The sample mean of the students’ score in the test was observed to be 28(while they listen to music). Under normal circumstances(without music), the scores of the test form a normal distribution with a mean of 25 and S.D of 6. Use alpha = 0.05 (one tailed test). Which of the following best represents a null hypothesis?
a) Listening to music while studying will not impact memory
b) Listening to music while studying may worsen memory
c) Listening to music while studying may improve memory
d) Listening to music while studying will not improve memory and might make it worse.
Ans: d) Listening to music while studying will not improve memory and might make it worse.
For more detailed explaination read here explaination 1 and explaination 2.
2) Numerous studies have demonstrated that listening to music while studying can improve memory. To demonstrate this phenomenon a researcher obtains a sample of 36 students and gives them a standardised memory test while they listen to music. The sample mean of the students’ score in the test was observed to be 28(while they listen to music). Under normal circumstances(without music), the scores of the test form a normal distribution with a mean of 25 and S.D of 6. Use alpha = 0.05 (one tailed test). Which of the following best represents an alternate hypothesis?
a) Listening to music while studying will not impact memory
b) Listening to music while studying will worsen memory
c) Listening to music while studying will improve memory
d) Listening to music while studying will not improve memory and might make it worse.
Ans: c) Listening to music while studying may improve memory
Since the null is “not improving memory and actually make it worse” the alternate should be “may improve memory”.
For more detailed explaination read here explaination 1 and explaination 2.
3) Numerous studies have demonstrated that listening to music while studying can improve memory. To demonstrate this phenomenon a researcher obtains a sample of 36 students and gives them a standardised memory test while they listen to music. The sample mean of the students’ score in the test was observed to be 28(while they listen to music). Under normal circumstances(without music), the scores of the test form a normal distribution with a mean of 25 and S.D of 6. Use alpha = 0.05 (one tailed test). What is your statistical decision? (Hint: Use z-test)
a) Reject the null
b) Accept the null
c) Can’t say
d) None of these
Ans: a) Reject the null. The standard error = 1 which gives the z-value (28 – 25)/1 = 3.
Clearly z = 3 has a p-value less than 0.05 so the null is rejected.
For detailed explaination read here.
4) Given the null hypothesis: that a process is producing no more than the maximum allowable rate of defective items. In this situation, a type II error would be:
a) to conclude that the process is producing too many defectives when it actually is not
b) to conclude that the process is not producing too many defectives when it actually is
c) to conclude that the process is not producing too many defectives when it is not
d) to conclude that the process is producing too many defectives when it is
Ans: b) to conclude that the process is not producing too many defectives when it actually is
A type II error is a statistical term used within the context of hypothesis testing that describes the error that occurs when one accepts a null hypothesis that is actually false.
For a detailed explaination read here.
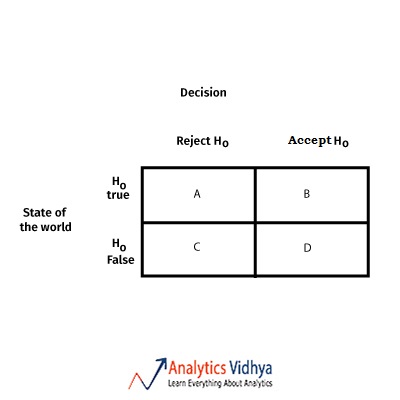
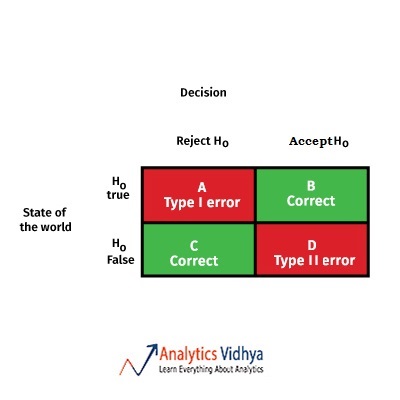
5) Which of these is known as Type 1 error
a) A
b) B
c) C
d) D
Ans: a) A
In statistical hypothesis testing, a type I error is the incorrect rejection of a true null hypothesis (a “false positive”), while a type II error is incorrectly retaining a false null hypothesis (a “false negative”).
For a detailed explaination read here.
6) If the P-value of a distribution is less than alpha, we can say that :
a) sample is not statistically significant
b) failed to reject null hypothesis
c) Sample is statistically significant
d) Insufficient data
Ans: c) Sample is statistically significant
When p-value is less than alpha, we reject the null hypothesis. In other words we have evidence to believe that the sample statistic is significantly different from the population parameter.
For further clarification read here.
7) Given a sample, which of the following tests can be used to determine whether the sample is statistically significant when population standard deviation is unknown
a) Z-test
b) t-test
c) F-test
d) a & b
Ans: d) z-test or t-test
Given a large sample z-test is used, whereas a t-test is used for for a small sample even if population parameter is unknown.
For detailed explaination read here.
8) Given a sample, which of the following tests can be used to determine whether the sample is statistically significant when the sample size is small (n<30)?
a) Z-test
b) t-test
c) F-test
d) a & b
Ans: b) t-test
For a small sample(n < 30) t-test is used.
For further clarification read here.
9) A hypothesis test is conducted and values of the sample mean and sample standard deviation when n = 25 are such that they do not lead to the rejection of H0. You calculate a p-value of 0.0667. What will happen to the p-value if you observe the same sample mean and standard deviation for a sample > 25?
a) Increase
b) Decrease
c) Stays the same
d) May increase or decrease
Ans: b) decrease
Increasing the sample size decreases the standard error, which in turn increases t-value/z-value thus decreasing the p-value.
10) Population mean = 50, Sample mean = 37, Standard Deviation of the Population = 10, Sample Size = 4. Taking alpha=0.05, can we reject the null hypothesis(two-tailed test)?
a) Yes
b) No
c) Can be rejected for all alpha
d) None of these
Ans: a)Yes
Standard error = 10/2 = 5. t-value = (50 – 37)/5 = 2.6, looking at the t-table with 4-1 = 3 degrees of freedom we reject the null hypothesis.
11) Students of the Chinese population have a mean learning rate of 7.47 with a standard deviation of 2.41. All the students of the Chinese population are provided with tablets so as to improve their learning rate. The Chinese government draws a sample of 50 students and found their new learning rate(after providing tablets) to be 8.3. Which box best fits the scenario, if the population learning rate after providing tablets was found to be 7.8 (a few years later)?
a) A
b) B
c) C
d) D
Ans: a) A
Standard error = 2.41/sqrt(50). The z-value of the sample can be calculated to be 2.44=((8.3 – 7.47)/SE). Which rejects the null hypothesis. Similarly the actual learning rate’s z-value can be calculated to be 0.97 which accepts the null hypothesis. This is a typical case of Type 1 error.
12) A two-tailed test is one where:
a) results in only one direction can lead to rejection of the null hypothesis
b) negative sample means lead to rejection of the null hypothesis
c) results in either of two directions can lead to rejection of the null hypothesis
d) no results lead to the rejection of the null hypothesis
Ans: c) results in either of two directions can lead to rejection of the null hypothesis
For a sample to be statistically significant(or synonymously rejecting the null hypothesis), the sample statistic can be either significantly lesser or greater that the population parameter. Hence c).
13) There are two schools namely DAV and St.Mary. Population parameters of marks of two schools are: Mean (DAV)=70.79, Mean (St. Mary)= 44.45, STDEV (DAV)=17.34, STDEV (St. Mary)= 26.17. Can you conclusively say that students of DAV score more than students of St. Mary(with 95% confidence level)?
a) Yes
b) No
c) Insufficient Data
d) Can’t say
Ans: a) Yes
Mean (DAV)=70.79
Mean (St. Mary)= 44.45
STDEV (DAV)=17.34
STDEV (St. Mary)= 26.17
Step1: Find the Mean difference of both school and combined standard deviation using formula
Mean difference = 70.79 – 44.45 = 26.34
n1 for DAV = 107
n2 for St Mary =140
Combined Standard Deviation = sqrt( 17.45*17.45/107 + 26.17*26.17/140) = 2.78
Step2: Calculate the Z value
Z= 26.34 / 2.78 = 9.47
Here Z value is very high, which makes the p value ~0 (look at the z-table). So yes we can say that students of DAV score more than students of students of St. Mary(95% confidence).
For more detailed explaination read here.
14) There are two schools namely DAV and St.Mary. Population parameters of marks of two schools are: Mean (DAV)=70.79, Mean (St. Mary)= 44.45, STDEV (DAV)=17.34, STDEV (St. Mary)= 26.17. Find the p-value of the difference of marks between the schools(closest value).
a) 0
b) 0.1
c) 0.2
d) 0.3
Ans: a) 0
As calculated in the above question.
15) What are the number of degrees of freedom for a N X N magic square
a) N^2
b) N-1^2
c) N * N-1
d) (N-2)^2
Ans: b) (N-1)^2
In a magic square the sum of rows and columns should add up to a specified number. So in a n X n magic square we are free to fill n-1 cells in every row and n-1 cells in every column so that the last number can be fixed in such a way that the row sum or the column sum sums up to the specified number.
16) For a t-distribution
a) The curve is wider than the population distribution curve
b) Curve becomes steeper on increasing the sample size
c) Curve becomes steeper on increasing the number of observations
d) All of these
Ans: d) All of these
a) Curve is wider because of high standard error as compared to a z-distribution.
b) Standard error reduces as sample size increases so curve becomes steeper.
c) Synonymous to (b)
So d) is the answer.
17) Consider the following sample: 1,2,3,4,5,6. Alpha = 0.05 and the population mean is equal to 4.5. Find the standard deviation for the sample to be used for calculating t-value.
a) 1.87
b) 1.95
c) 2.03
d) 2.53
Ans: a) 1.87
Standard deviation = sqrt(sum((mean – observation value)^2)/number of observations)
18) Consider the following sample: 1,2,3,4,5,6. Alpha = 0.05 and the population mean is equal to 4.5. Which of the following is true?
a) Sample lies is the critical region of the t-distribution.
b) sample does not lie in the critical region of the t-distribution.
c) May or may not lie
d) None of these
Ans: b) sample does not lie in the critical region of the t-distribution.
Case 1: Two Tailed:
Critical Value of t = -2.571 or 2.571
Case 2: One Tailed:
Critical Value of t = -2.015 for left sided or 2.015 for right sided
t Statistic = -1.309
Therefore, in either of the cases the t Statistic does not lie in the critical region.
19) Consider the following sample: 1,2,3,4,5,6. Alpha = 0.05 and the population mean is equal to 4.5. The cohen’s d is given by:
a) -0.65
b) -0.53
c) -0.44
d) -0.78
Ans: b) -0.53
Cohen’s d = (sample mean – population mean)/standard deviation, which can be calculated to be -0.53
For further explaination read here.
20) Consider the following sample: 1,2,3,4,5,6. Alpha = 0.05 and the population mean is equal to 4.5. Calculate the coefficient of determination for this data.
a) 0.36
b) 0.31
c) 0.25
d) 0.22
Ans: c)0.25
r-squared/coefficient of determination = 1 – RSS/TSS
Where RSS(Residual sum of squares) = sum((mean of sample – observation)^2) and
TSS(Total sum of squares) = sum((population mean – observation)^2)
For further explaination read here.
21) Consider the following sample: 1,2,3,4,5,6. Alpha = 0.05 and the population mean is equal to 4.5(two-tailed test). Calculate the margin of error for the sample.
a) 0.5
b) 1
c) 1.5
d) 2
Ans: c) 1.5
Margin of error = critical value * standard error
standard deviation = 1.87 , standard error = 1.87/sqrt(6) = 0.76
Critical value = 1.96 (for alpha = 0.05 in two tailed test)
Margin of error = critical value * standard error = 1.5
22) What is the degree of freedom for between group variability of k samples in a population of n elements?
a) n-1
b) n
c) n-k
d) n-k-1
Ans: c) n-k
Since the variability is k, the degree of freedom should be n-k.
23) Calculate the r-square value for a sample with t-value of 1.5 and 35 size
a) 0.04
b) 0.05
c) 0.06
d) 0.07
Ans: c) 0.06
r-squared = t^2/(t^2 + df)= 2.25/(2.25 + 35) = 0.06
24) F-test is a unidirectional test to compare samples of a population.
a) True
b) False
c) Cannot be determined
Ans: b) False
F-test is not a uni-directional test.
25) Which can be considered as an effect size indicator?
a) r-squared
b) r
c) eta-squared
d) all the three
Ans: d) all three
All three given quantities are measures of effect size.
26) A statistical test used to compare two or more means is called ?
a) one way analysis of variance
b) t-test for correlation coefficients
c) chi-square test for contingency tables
d) None of these
Ans: a) ANOVA
Among the given tests only ANOVA can compare two samples, although t-test can also be used but it isn’t mentioned here.
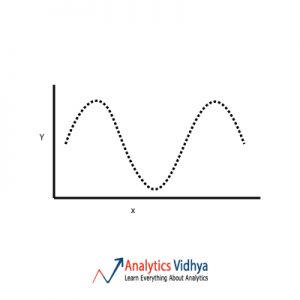
27) Given the following plots of two variables, which among the plots suggest a non-correlation between the variables?
d) None of these
Ans: d) None of these
The common misconception is that correlation is considered as ‘linear correlation’ and c) could be thought to be the right answer. But those variables have a trigonometric correlation.
28) GPA scores of two samples of students are given below. Sample A is the scores of students who sleep for around 8 hours a day and Sample B is the scores of students who slept around 6 hours a day. Sample A: 5,7,5,3,5,3,3,9. Sample B: 8,1,4,6,6,4,1,2. The School tries to study the impact of sleep on scores. Which tests would help us identify the impact of sleep?
a) t-test
b) ANOVA
c) chi-squared
d) both a & b
Ans: d) Both t-test and ANOVA can be used
Two samples can be compared by one way analysis of variance or two sample t-test.
29) GPA scores of two samples of students are given below. Sample A is the scores of students who sleep for around 8 hours a day and Sample B is the scores of students who slept around 6 hours a day. Sample A: 5,7,5,3,5,3,3,9. Sample B: 8,1,4,6,6,4,1,2. The School tries to study the impact of sleep on scores. What are the degrees of freedom to test this hypothesis?
a) 7
b) 8
c) 14
d) 15
Ans: c) 14
degrees of freedom = Size of sample A + Size of sample B – 2.
30) GPA scores of two samples of students are given below. Sample A is the scores of students who sleep for around 8 hours a day and Sample B is the scores of students who slept around 6 hours a day. Sample A: 5,7,5,3,5,3,3,9. Sample B: 8,1,4,6,6,4,1,2. What is the t-value(closest value)?
a) 0.847
b) 2.146
c) 6.614
d) None of these
Ans: a) 0.847
MeanA (Mean of Sample A) = 5
S1 (standard deviation of Sample A) = 2.138
MeanB (Mean of Sample B) = 4
S1 (standard deviation of Sample B) = 2.563
n1 =n2 = 8
t-statistic for two samples is given by (MeanA – MeanB)/sqrt(S1^2/n1 +S2^2/n2) = 0.847
For detailed explaination read here.
31) GPA scores of two samples of students are given below. Sample A is the scores of students who sleep for around 8 hours a day and Sample B is the scores of students who slept around 6 hours a day. Sample A: 5,7,5,3,5,3,3,9. Sample B: 8,1,4,6,6,4,1,2. Does sleep affect GPA?
a) Yes
b) No
c) Not enough data
d) Can’t conclusively say
Ans: d) Can’t conclusively say
We can never conclusively say, we only have evidence to support our claim.
32) The chi-square goodness-of-fit test can be used to test for:
a) significance of sample statistics
b) normality
c) difference between population means
d) probability
Ans: b) Normality
Chi-squared test is a test for normality.
For further explaination read here.
33) The ANOVA test is based on which assumptions?
a) the sample are randomly selected
b) the population variances are all equal to some common variance
c) the populations are normally distributed
d) b and c
Ans: d) b and c
The ANOVA test being a frequentist test always assumes population parameters to be fixed and the population to be normally distributed.
For further explaination read here.
34) The chi-square test can be too sensitive if the sample is:
a) very small
b) very large
c) homogeneous
d) non-homogeneous
Ans: b) very large
Chi-square test has limitations, one such is sample size.
For detailed explaination read here.
35) One way ANOVA is used when:
a) analysing the difference between more than two population means
b) analysing the difference between two population means
c) analysing the results of a two-tailed test
d) analysing the results from a two tailed test
Ans: a) analysing the difference between more than two population means
For further clarification go through this video.
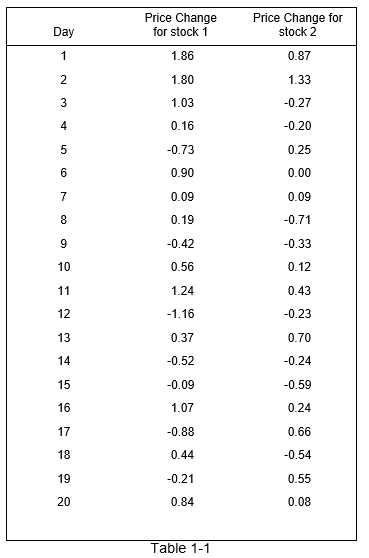
36) An investor obtains a random sample of 20 daily price changes for stock 1 and 20 daily price changes for stock 2. He wants to compare whether the stocks are similar in nature. These data are shown in the table below. Use alpha = 0.10. With have evidence to believe that the stocks are:
a) Not similar with p-value < 0.025
b) Similar with p-value > 0.2
c) Not similar with a p-value between (0.02 to 0.1)
d) Similar with p-value between 0.1 to 0.2
Ans: a) not similar with a p-value < 0.25
n1 = 20, s1 = 0.8487, n2 = 20, s2 = 0.5291
Null hypothesis: (sigma1^2/sigma2^2) = 1
Alternate hypothesis: (sigma1^2/sigma2^2) is not equal to 1
F-statistic = sigma1^2/sigma2^2 = 2.573
P-value=0.023
Since the P-values is less than 0.10, we reject the null hypothesis of equal variances and conclude that the variances of the stocks are not equal at the 10% level.
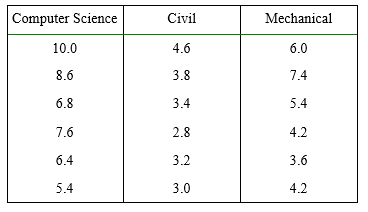
37) Given are yearly salaries of 18 recent graduates from 3 different departments. At the 0.05 level of significance, is there evidence of a significant difference in average salary among the various departments?(Select the most appropriate option).
a) Yes, with a p-value < 0.05
b) Yes, with a p-value < 0.005
c) Yes, with a p-value < 0.0005
d) No, with a p-value > 0.05
Ans: c) Yes, with a p-value < 0.0005
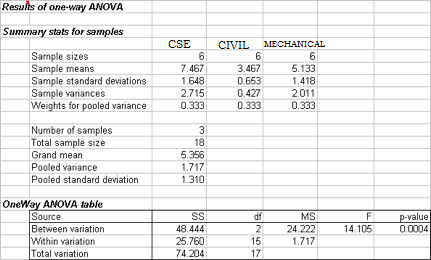
To test at the 0.05 level of significance whether the average salary is different across the three departments, we conduct an F test:
H0: u1 = u2 = u3
H1: At least one mean is different.
Since p-value = 0.0004 < alpha = 0.05, we reject H0. There is enough evidence to conclude that the average sales volumes in thousands of dollars are different across the three store aisle locations.
38) Adding more variables to a linear model will
a) Increase or not change the R-squared value
b) decrease the R-squared value
c) not change the R-squared value
d) None of these
Ans: a) Increase or not change the R-squared value
Adding more variables can increase or not change the R-squared value
39) The following data lists eight different investment amounts (X) and the amount of interest they earned (Y). For the linear model Y ~ X the R-squared value will?
| X(Rs.) |
1000 |
3000 |
10000 |
5000 |
2000 |
500 |
| Y(Rs.) |
50 |
150 |
500 |
250 |
100 |
25 |
a) positive and close to zero
b) positive and close to one
c) exactly one
d) negative
Ans: c) equal to one
It is evident that the regression co-efficient is 1. Still formulas application will give the same result.
For further explaination read here.
40) In the above data, the sector of each investment is added. When compared to the R-squared value of the linear model Y ~ X, the multiple R-squared value of the model Y ~ X + Z will ?
| X(Rs.) | 1000 | 3000 | 10000 | 5000 | 2000 | 500 |
| Y(Rs.) | 50 | 150 | 500 | 250 | 100 | 25 |
| Z | Automobile | FMCG | FMCG | Automobile | Healthcare | Electronics |
a) increase
b) decrease
c) remain the same
d) insufficient data
Ans: c) remains the same
Since variables Y and X already correlated with R-squared value 1 (the maximum value), adding a new variable won’t impact the model.
End Notes
How was your experience taking the second skill test in Statistics? This time the enthusiasm was double and the eagerness to take the second challenge in Statistics was immeasureable. In the above article we tried to answer all your queries but if you have any doubts / confusions in any question then bombard the comments with all your queries and we will be happy to answer them. Don’t forget to share your feedback with us, because how will be improve if you don’t tell us what to change.
If you are a Python practitioner then you must register for the upcoming Skilltest – Python for Data Science.
Do you know good probability skills are your sure shot way to develop strong data analysis techniques? Take our unique probability workshops AV Casino I and AV Casino II.








Query about Q. 13. How did you get n1 for DAV = 107 n2 for St Mary =140 Query about Q.22 Can you explain how you calculated degree of freedom. As per what I understand, if there are k no. of samples, then the d.f of "between samples" would be k-1 And, if the sample size per sample is n then the "within sample" d.f is (n-1)k https://youtu.be/M-MBHLSRKzw Thanks!
Sorry about that. With thorough embarrassment I admit my mistake of not having updated the values of degree of freedom in question 13 and 14. I'll ensure that this doesn't happen in the future.
For Q22), Since there are k-samples, each sample might be any size but they all sum up to the population n. For each sample we can reduce 1 to calculate the degree of freedom of each sample and when we sum all the degrees of freedom we get it as n-k. Regards
Hi, Can you please explain in q13 answer how you got, n1 for DAV = 107 and n2 for St Mary =140 Thanks
Sorry guys. With thorough embarrassment I admit my mistake of not having updated the values of degree of freedom in question 13 and 14. I’ll ensure that this doesn’t happen in the future.
For Q-13 and 14 , n1 and n2 values were not given ? How can you use it in solutions ?
For Question 18: Case 1: Two Tailed: Critical Value of t = -2.571 or 2.571 Case 2: One Tailed: Critical Value of t = -2.015 for left sided or 2.015 for right sided t Statistic = -1.309 Therefore, in either of the cases the t Statistic lies in the region of Non - Rejection. So, should the correct option be b? Please let me know what I am missing here.
Hi Kenneth, Thanks for pointing out the mistake. Will edit accordingly.
Can you please clarify on Question number 22. As per as i understand the degree of freedom should be n- k -1 .
For Q22), Since there are k-samples, each sample might be any size but they all sum up to the population n. For each sample we can reduce 1 to calculate the degree of freedom of each sample and when we sum all the degrees of freedom we get it as n-k. Regards
very very useful stuff, plz try to plan for a second test in R and third one Statistics. and, plz provide the answer and its formula derivation for AV casino 1 last(satan) question. (12 people sitting around a round table). We need to know the formulas/solutions figured out by us is correct or wrong. (I get 9!)
Hi Scratching my head over Q10. The p value is between 0.05 and 0.1. Hence greater than 0.05. And hence the Null hypothesis cannot be rejected - right? But the solution says - rejected. Am i missing something. Thanks
I'm sorry but I think you got the question number wrong. Please mention the right question number.
@Amit Srivastava: Ans to Q.31 A t-test at Alpha=0.05 suggests that the null hypothesis cannot be rejected is TRUE. But i would like to make little change in H0: There is no difference between the GPA score of two samples A and B.
I have a question for 10; its a 2 tailed test with critical values -3.18 and +3.18 and the statistic value is 2.6, which is between the 2 critical values; so we should accept the null hypo at 95%CI? Correct me if wrong please.
for ques 22, the df for between groups should be k-1 for k samples; n-k is the df for within group variability and not between?
I think answer for ques 29 should be 15 for df of total ie n-1 ie 16-1 and not 14. df for within groups can be 14 ie n-k ie 16-2 (k is no of samples)??