Introduction to Bayesian Adjustment Rating: The Incredible Concept Behind Online Ratings!

Overview

• Curious how the big product companies like Amazon, Walmart, AirBnb, etc. manage the ratings we see?
• The core idea behind these ratings systems is a concept called the Bayesian Adjusted Rating
• We’ll discuss this Bayesian Adjustment Rating and the intuition behind it here

Introduction

Do you always look at the rating and the number of ratings of a product before you buy it? I honestly rely a lot on these factors when I’m scouring e-commerce sites or other similar product portals. It is my default go-to option to evaluate the product before I go all in.

And these ratings aren’t just limited to e-commerce portals. We now see them across the internet on various channels, like:

• Blogs
• News sites
• Hotel reviews
• Food reviews
• Movie reviews, and so on.

I’ve always been curious about how these rating systems work. The data science professional in me wanted to figure out if it was a simple average calculation or was there more data science involved here?

The results of my research are quite fascinating, as we will see in this article. So let’s dive into it.

Note: Here’s an intuitive article on Bayesian Statistics if you’re looking to understand the topic (or need a quick refresher):

• An Introduction to the Powerful Bayes’ Theorem for Data Science Professionals

Table of Contents

• Setting up the Problem Statement for our Rating System
• The Ubiquitousness of Social Influence
• In the Star Ratings, I Trust
• Sorting the Star Ratings using Bayesian Adjusted Rating

Setting up the Problem Statement for our Rating System

Suppose you are a blogger and you want to put your top three pieces in popularity order at some easy to view area on your beautiful web page. You want to use the number of ‘likes’ and ‘shares’ your subscribers have provided on your blogs in order to sort them. And you wonder if a simple average is what you should use as some of your newer blogs have barely reached sufficient views.

The fact is, a lot of websites are grappling with exactly the same perplexity but on a much larger scale. And getting this ‘sorting’ right is equally important for your brand as a blogger, as much as it is incrementally useful for your subscriber community.

The Ubiquitousness of Social Influence

Online social networks are not just limited to a few dedicated websites or applications that enable users to create and share content but are present everywhere on the internet. These collaborative virtual communities expose persuasive effects people have on each other in the form of social influence. It can take many forms and can be seen in conformity, compliance, peer pressure, obedience, persuasion, as well as sales and marketing.

Participating in online customer ratings and reviews is very much a social network of people with a similar product or service interest.

End-users of products or services on the web communicate within themselves using the language of ‘stars’ and ‘likes’ buttons and occasional text reviews.

It is unquestionably at par or more actionable than any other network we may think of.

‘People’ constitute both the core and the clientele for any Rating or Reputation system no matter what the overarching platform it is meant for. It can simply be a review forum (Yelp, IMDb or Beer Advocate), a sharing economy (like Airbnb or Uber), a marketplace (Amazon, Flipkart or Swiggy), or even China’s upcoming Social Credit System.

In the Star Ratings, I trust

Ratings are so much built into our psyches that the ‘trust’ is not an obstacle with them anymore. We believe in them subconsciously, we take trade decisions based on them, and we genuinely invest in them with our personal choices.

So why are ratings so fundamental to our choices? Why do we trust them with our time, money and emotion? We can fairly assume that these ratings create a sense of transparency and validation of our own decisions and serve the same efficiently through one convenient scalar value.

Condensing hundreds of ratings from respective user communities into one exclusive rating value which can epitomize the essence of diversity is as much a field of art as it is science. There is a skill, a mastery of how certain businesses have used them so effectively.

For them, it’s a secret sauce, kept such so as to eliminate and reduce attempts by people more interested in changing the current rating than giving their true opinion of it.

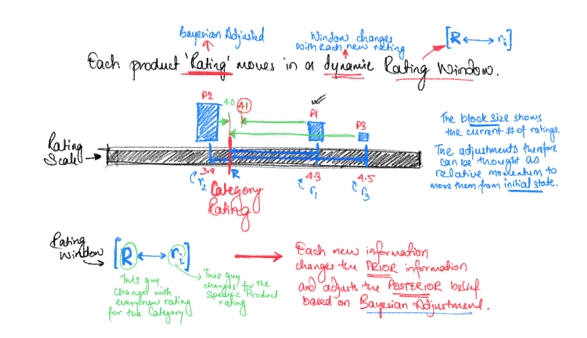
Sorting the Star ratings using Bayesian Adjusted Rating

The philosophy to rank competing products of the same category on a marketplace like Amazon is to make the ranking appear natural; And for that to happen, the sorting metrics (i.e. our scalar rating value for each product) should inherit the essence of the ‘number of reviews’ it has received relative to the overall category.

Thus, we start with how that specific category, as a whole, has been rated by the users.  And then we change our strategy from the ‘Simple Average Rating’ to ‘Bayesian Adjusted Rating’ in order to incorporate the variation in the number of reviews to our product ranking.

This shift to the Bayesian approach provides the comfort of staying consistent even when we have fewer observations. This is because then it is very likely to obtain extreme values just by chance.

Let’s say we want to find the best product out of 3 options in a category. Here’s how I have calculated it by hand:

Eventually, what any new user would care about is how intuitive the ranking is based on what they can observe (i.e. the rating and number of reviews for each product of that category) and now that we can see all the individual data it will make us trust the website more if we see the best product with the smallest probability to being poor quality.

And this intuition is what Bayesian Adjusted Rating formalizes.

Going back to ranking the blogs using some kind of rating derived from the combination of views, likes, and shares, we observe that the simple ranking gives weight to the % of likes and % of shares.

For interested viewers, my article ratings are weighted averages of likes, shares, and views.

Where,

We won’t dive into the details of the calculation as my aim here is to introduce you to the Bayesian Adjusted Rating concept. If you’re interested in the math behind it, I encourage you to check out resources available online (and there are many).

Here, we will jump right to the core of the Bayesian Adjustment to our Rating System:

We can then use the new Bayesian Adjusted Ratings to calculate the new ranking. This gives us a more intuitive ranking of the articles compared to the simple average rating.

At this point, I would encourage you to pick up a small dataset and try out this concept on your own. Learning the theoretical aspect of data science is good but you won’t truly appreciate it’s value till you actually see it in action. Let me know how your experiments go in the comments section below this article. Would love to discuss further there!

Summarizing what we learned here

So, let’s quickly summarize what we have covered here.

What is our concern?

When we have one or more products with very few ratings, how do they compare to products whose ratings are known with a high level of certainty?

What’s the fix?

Knowing that some products have a higher number of reviews and ratings compared to others, we may think about it as a sliding ruler where, if a product has a lot of reviews, I should trust its own average. But if it got too few reviews relative to others, then I should pretend as if it is an average product across the entire category.

And this is exactly what the Bayesian Adjusted Rating does, it shifts the rating somewhere between the simple average of that product and the overall category depending on how much we can trust its own rating.

My top two blogs should be my Article #s 3 and 5 respectively based on the pseudo counts of the ‘likes’ and ‘shares’ I have received from their views.

What are your thoughts on this rating system? Have you seen it in action yourself? I look forward to hearing your thoughts and feedback below!

About the Author

Abir Mukherjee

Abir Mukherjee is a research analyst with over a decade of experience in managing credit card marketing, customer servicing, and business development projects. He has worked on multiple analytical solution deliveries for the US market as a part of both onshore and offshore teams. He is a strong believer in simple, contextual and value-driven solutions.

Abir has a Masters degree in Industrial Engineering from IIT Kanpur. He earned his Bachelors in Information Technology. Currently based out of Bangalore and is originally from Singrauli, Madhya Pradesh.

Outside of his work Abir enjoys painting and graphic design; And fond of traveling to explore new cuisines and cultures.