Overview
- What is Game Theory? And how does it apply to artificial intelligence (AI)?
- Game theory for AI is a fascinating concept that we feel everyone should at least know about
- Here, we take an in-depth look at Game Theory using illustrated examples and relate it to AI
Introduction
I want to start off with a quick question – can you recognize the two personalities in the below image?
I’m certain you got one right. For most of us early age math enthusiasts, the movie “A Beautiful Mind” is inextricably embedded into our memory. Russell Crowe plays the role of John Nash in the movie, a Nobel prize winner for economics (and the person on the left-hand side above).
Now, you would remember the iconic scene often regarded as: “Don’t go after the blonde”. In this scene, John Nash quotes:
“….the best outcome would come when everyone in the group is doing what’s best for himself and the group.”
Many people regard this scene as the discovery of the famous “Nash Equilibrium”. While definitely iconic, it’s not quite true. The scene actually depicts the discovery of “Pareto Optimality”. But it will help us nevertheless in our understanding of Game Theory.
So in this article, we will take a bird’s eye view of Game Theory. We will also discuss the underlying idea of how Game Theory is being used in the field of Artificial Intelligence (AI). I have written this article in a way that even beginners and non-technical folks can follow along. So strap in and enjoy the learning experience!
Table of Contents
- What Is Game Theory?
- Nash Equilibrium in Game Theory
- Types of Games
- Game Theory in Artificial Intelligence (AI)
- Pop Quiz on Game Theory!
So let’s dive right into it.
What Is Game Theory?
So, what is game theory? I’m sure you’ve come across this concept at some point but never truly dived into it. Trust me, it is an intriguing topic and an enlightening one in the artificial intelligence space.
Let’s put a formal definition to Game Theory first.
Game Theory can be referred to as the modeling of the possible interactions between two or more Rational Agents or players.
Here, I must stress upon the keyword “Rational” as this acts as the foundation of Game Theory. But what exactly does Rationality mean?
We can simply call rationality as an understanding that every agent knows that all the others are just as rational and hold the same level of understanding and knowledge as he/she does. Also, Rationality will refer to the fact that agents would always prefer the higher reward/payoff considering what other agents will do.
In short, every agent is selfish and tries to maximize the reward.
Now that we know what rationality means, let’s tackle some other keywords associated with game theory:
- Game: In a general sense, a game comprises of a set of players, actions/strategies and the final payoff. Example: Auction, Chess, Politics, etc.
- Players: Players are rational entities that participate in any game. For example:
-
- Bidders in an auction setting
- Players playing rock-paper-scissors
- Politicians participating in elections, etc.
- Payoff: Payoff is the reward that all the players get when a certain outcome is achieved. It can either be positive or negative. As we discussed before, each agent is selfish and wants to maximize their payoff:
The Nash Equilibrium in Game Theory
Nash equilibrium is the “Bedrock” of the Game Theory approach to Artificial Intelligence. Nash Equilibrium is an action chosen by each player such that:
“No player would want to change their action. Changing their action from Nash Equilibrium means they are not playing optimally”
or
“Considering that all other agents are rational and choose the best action for themselves, Nash Equilibrium action for me is the best response.”
No player can increase payoff by changing decisions within their action set. We can also think of it as “no regrets” in the sense that once a decision is made, the player will have no regrets concerning decisions considering the consequences.
To see Nash Equilibrium in action, let’s now tackle the most common problem of Game Theory, The Prisoner’s Dilemma. This game is a classic example and illustrates the difficulty of acting together cooperatively for common or mutual benefit in scenarios where agents are only concerned about their self-interest.
In this game, we have two prisoners, Alan and Ben, who were caught for the same crime and are held in two different interrogation rooms. They’ve been given two choices:
- Stay silent
- Confess to the crime
Let’s say that each of them is given two choices. So, there would be 4 outcomes in total:
- {Silent, Silent}
- {Confess, Silent}
- {Silent, Confess}
- {Confess, Confess}
And these 4 outcomes can be conveniently represented as a game matrix:
In this representation, the payoffs are represented in the form of (Alan’s Payoff, Ben’s Payoff). Along the rows, we have the actions of Alan, and along the columns, we have the actions of Ben.
I suggest taking a good look at the payoffs. Why do you think the payoffs are negative? This is because based on their actions, they will receive a predetermined number of years of imprisonment (which is not at all desirable).
Following the results of the outcome:
- If both of them remain silent, both of them get imprisonment for a year
- If either one of them confesses, the confessor walks free and the other prisoner gets 15 years of imprisonment
- If both of them confess, both of them receive imprisonment for 10 years
The dilemma comes in because neither prisoner is aware of what the other prisoner did. So, what do you think is the Nash Equilibrium action in this problem? It is very intuitive to think that prisoners would collaborate with each other and stay silent.
But then we also know that prisoners have evident self-interest in minimizing the imprisonment they receive. And even if they remain silent, they still get imprisonment of a year each.
So what actually happens is this:
Now, this is something Ben would also be thinking. If we focus on the game matrix, the thinking process would make perfect sense:
- In the case where Ben confesses, Alan’s best choice is to confess. This will lead to lesser punishment of 10 years rather than 15
- In case Ben stays silent, Alan is still better off confessing as he will be a free man instead of facing one-year imprisonment if he also stays silent
So this game matrix is in perfect congruence with what Alan is thinking. Now, if Ben is also thinking the same, the Game matrix would look like this for him:
Let’s say that Ben also goes through the rational thought process as Alan. Ben also comes to the conclusion that no matter what Alan chooses, he will always benefit from confessing. Now, if we superimpose the Rational thinking of both these prisoners, the result is something like this:
And looking at the results, the best strategy comes out to be {Confess, Confess}. Even if either of them tries to deviate from this action, they are worse off than what they are getting by playing this action. Hence, {Confess, Confess} is a Nash Equilibrium strategy.
Makes perfect sense, right? For Nash Equilibrium, we can conclude that it is a “No Regret” solution for any game, but not necessarily the most optimal one.
Types of Games
We just saw an example of Prisoner’s Dilemma where two prisoners had to make a simultaneous decision which we represented in the form of a game matrix. These types of games are often referred to as Normal form games.
In Game Theory, games can be divided into many different categories based on many different criteria.
Let’s take a look at them in detail.
Interaction Between Agents
Intuitively, we can differentiate the games on the basis of whether the agents in that game are aiming to compete or cooperate.
Political campaigns are good examples of competitive games where the reward for one candidate results in a loss for another candidate. On the other hand, a basketball game can be regarded as a cooperative game, where each player gets more reward if they cooperate with each other.
How Agents Play
We can also classify games based on whether they are simultaneous or extensive in nature.
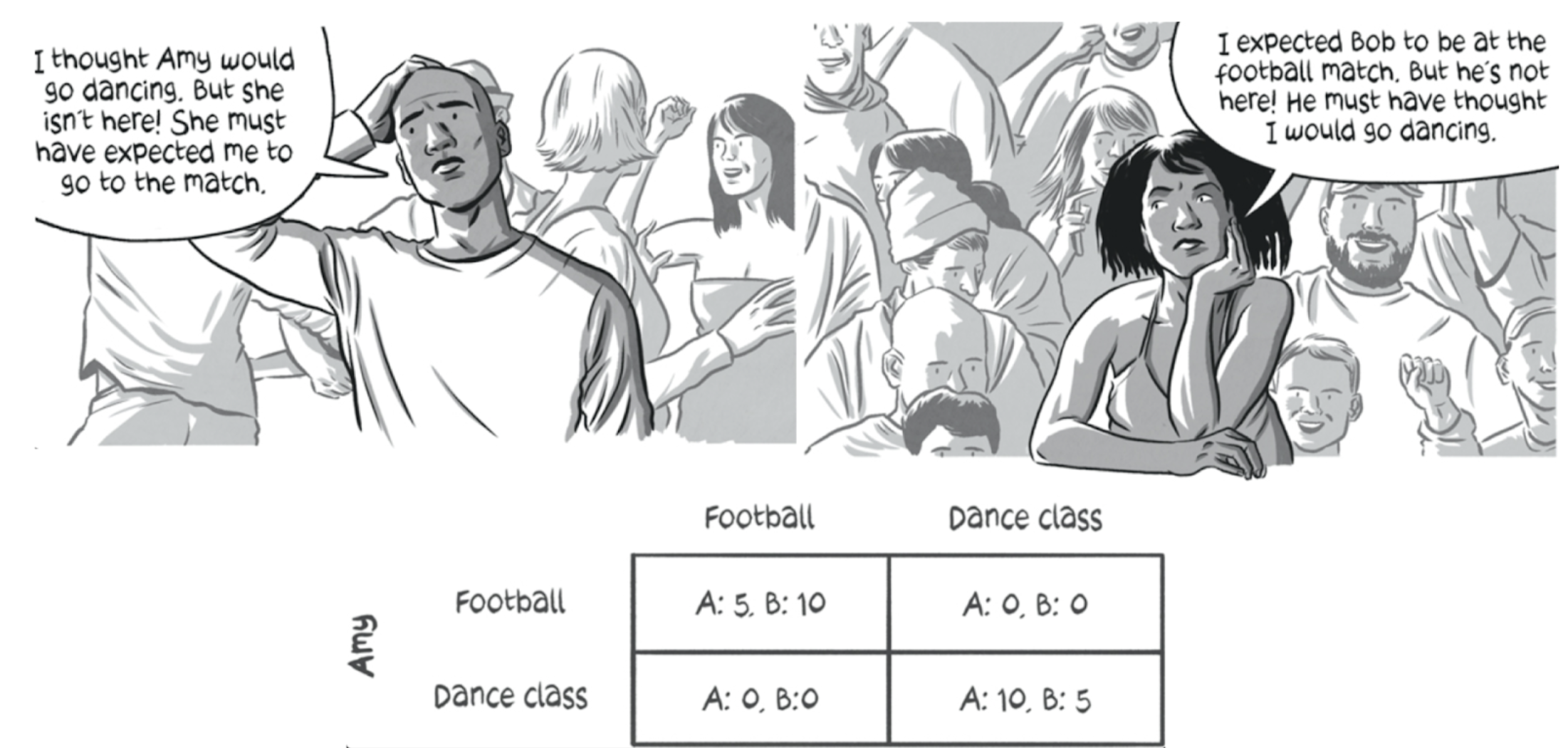
To understand this let’s take an example of a problem called “Battle of the Sexes”.
Consider that Bob and Amy are two friends who are fond of each other’s company. They are well aware of each other’s habit of going out for football games and dance parties respectively. They decide to accompany each other so they can either discuss it with each other or just surprise each other.
If they plan on surprising each other, they are unaware of each other’s plans for the weekend. This ends in 4 different situations as depicted by the game matrix:
The game matrix clearly explains that both Bob and Amy get no payoff if they miscoordinate with each other. This is an example of a simultaneous game where both players make simultaneous moves and are unaware of other player’s actions in advance.
On the other hand, if they coordinate with each other by telling each other their actions, the game takes the following form:
This is a case of an extensive form game or a “Turn-Based Game”. Here, each player can see what actions the other player is playing.
Here’s another intuitive example – the game of Rock-Paper-Scissors is a good illustration of a simultaneous game. On the other hand, the game of Tic-Tac-Toe is an extensive form game.
On the Basis of Information
In Game Theory, situations often arise where players have incomplete information. They might not know all of the other player’s available strategies or potential payoffs. Players might not be aware of what kind of person they are dealing with or what their motivations are.
Games can be broadly divided into three types depending on how much they know about their other agents:
- Perfect information
- Imperfect information
- Incomplete information
Perfect Information:
In perfect information, every agent has knowledge of:
- All the possible actions the other agents can take
- What actions they are playing
- How much reward they get for outcomes
Tic-Tac-Toe and chess are perfect examples of this. Perfect information games are very rare when it comes to the real world. Also, machine learning and deep learning approaches work very well in these games.
Imperfect Information:
In this case, agents are aware of the nature and motive of the other agents and how much payoff they will get in all the possible outcomes. But they do not know what actions they are playing.
Here, the General knows about the motivation and the payoff of the enemy in each possible scenario. But he does not know where the enemy is hiding. As a result, the General is unaware of the exact decision node he is at (represented by the dotted box). Imperfect information games are often encountered in real-world scenarios.
Incomplete Information:
Incomplete information is a situation that models the real world very closely. Here, agents do not have information about the “TYPE” of other agents.
Even if any given agent is able to see the actions taken by the other agents, he/she does not know about the motivation of the other agents or what reward the other agents will get for playing that action.
In essence, incomplete information games are the most generalized form of games.
Poker is a classic example of an imperfect information game because a player does not know whether the opponent is holding a good or a bad pair of cards.
We are especially interested in the game of poker because it represents the real world very well due to its nature of incomplete information. Because of this, it has long been regarded as a benchmark problem in the field of Artificial Intelligence (AI) for imperfect information games.
Game Theory in Artificial Intelligence (AI)
Ah – you must have been wondering what all of this means in the context of artificial intelligence. What do these different types of Games and Information have to do with AI? Well, let’s find out!
Game Theory, in terms of AI, basically helps in making decisions. This is not very difficult considering the fact that “Rationality” is the foundation of Game Theory. As a matter of fact, Game Theory has already started establishing its place in Artificial intelligence – can you guess where?
One such niche is the concept of Generative Adversarial Networks (GANs). They have been quoted as:
“The coolest idea in machine learning in the last twenty years.”
by Yann LeCun, one of the leaders in the field of Artificial Intelligence and Deep Learning. So how does Game Theory help GANs?
To answer that, we need to first understand the basics of GANs. A GAN is a combination of two neural networks, namely:
- Generator
- Discriminator
A generator is a neural network that generates random images. On the other hand, a Discriminator tries to classify whether the generated image belongs to the given dataset or if it’s a generated image.
If the image is classified as “generated” or the fake image is caught by the discriminator, the Generator network adjusts its parameters. On the other hand, if the “Discriminator” classifies the generated fake image as one from the dataset, then the “Discriminator” adjusts its parameters.
This competitive process goes on until a state is reached where there is no more scope of improvement. This state is called the “Nash Equilibrium”. Surprised?
This is, in essence, a competitive game between two neural networks. Although in this case, they are continuously optimizing themselves to find a Nash Equilibrium.
Game Theory’s core implementation lies in the games of imperfect information. As we have already discussed, Poker is one of the classic examples and a proper benchmark problem for AI applications in Imperfect information.
Imperfect information is very important because real-world problems often fall under this category. So far in the history of AI, machine learning and deep learning approaches have had very limited success when it comes to incomplete information games.
One such game is the no-limit Texas hold ’em version of Poker. This is an imperfect information game as the opponent player has hidden information in the form of cards he is holding. This is a very challenging problem considering the fact that this poker version has 10 to the exponent of 161 states in the game.
Or, in other words, 10 to the exponent 161 total different possibilities in the game. To put this into context, the number of total atoms in the observable universe is 10 to the exponent 82!
So, modeling this game using brute force is simply out of the question. Also, there have been attempts made using Deep Learning and Deep Reinforcement Learning, but the results have been mediocre so far.
But an AI program called Libratus developed by Professor Tuomas Sandholm and AI researcher Noam Brown from Carnegie Mellon University has outperformed any previous methods so far. Libratus has trumped world champions in over 20,000 hands of poker. The amazing thing about Libratus is that it does not use any Machine Learning methods whatsoever!
Game Theory is the key idea behind Libratus. It uses relatively low computing power as compared to Deep Learning or Reinforcement Learning methods. To know more about how Game Theory was used in the development of Libratus and Game Theory as a part of Artificial Intelligence in the future, I highly recommend the Artificial Intelligence podcast between Lex Fridman and Tuomas Sandholm:
Game Theory approaches are gradually gaining momentum because of their generalizability in real-world use cases. The best example would be the work undertaken by Milind Tambe who is the director of “AI for Social Good”. Using the concepts of Game Theory, Milind Tambe handles real-world issues like:
- Public Safety
- Wildlife Conservation
- Public Health, etc.
I would definitely recommend checking out this video on how Professor Tambe tackled real-world problems related to the above-mentioned applications using Game Theory. Five minutes into the video, you will get a glimpse of how Game Theory can be implemented in real-world use cases:
Pop Quiz on Game Theory!
Phew – we’ve discussed Game Theory at length here. Let’s wrap up things with a quick pop quiz! It’s a good way to revise what we’ve learned in this article (and put that into practice).
You need to randomly pick a number between 0-100. The winner is the person who picks 2/3rd of the average of all the numbers answered in this quiz. Can you answer this question?
Hint: Consider that every other agent is as rational as you are.
You can submit your response here!
End Notes
In this article, we discussed the fundamentals of Game Theory and covered the essential topics in brief. We even spoke about how Game Theory is being used in the field of Machine Learning and its real-world implementations.
This was an introductory piece – we will go much deeper into Game Theory and how to apply it in the Artificial Intelligence space in a future article where I will take a technical perspective.
Do you have any questions on Game Theory? Have you ever applied it yourself in AI or any other domain? I would love to hear your thoughts and feedback in the comments section below.
Note: Most of the images were taken from the book – Ivan Pastine. “Introducing Game Theory”.





























But hey, that's just a theory....a GAMMEEE THEORRYYYYY
xD Although it is widely used in conjunction with Data Analysis.
Hi i am beginner so that is good thing for a beginner to learn these things
Game Theory is essential for people who are working in the field of Reinforcement Learning, only implementable for advanced use case, I would not recommend investing time into this if you are a complete beginner. Although the article in introductory and there is no harm in learning the basics.
Great article for beginners. The most important question I have is - where do you get those beautiful illustrations from? Did you create them yourself?
this article is really inspiring. thanx for sharing. I guess this methode can challenge IBM deep blue machine in chess competition
Appreciate your feedback. Deep Blue is based on GOFAI (Good old Artificial Intelligence), or in other words based on brute force search and alpha-beta pruning (not really intelligent). Just to point out, chess is a game of perfect information(each player can see everything). As a result, it is not that difficult to solve. Game Theory shines in the field of imperfect information, POKER is a classic example of this. GOFAI, Deep LEarning and Reinforcement learning have had very limited success with Poker whereas Game Theoretic approach mastered the game.
It's really great article and helpful for me.......Please keep it up.....
Nice Information!!!! Please keep it up
IA is a kind of tech trend and most people understand AI as a magical touch. Just like Game Theory, most of the predictive approaches are related to probability and simulation science. Also, Heisenberg's Uncertainty Theory tells us there are not any ignorable numbers or details contrary to Newtonian physics...