How to Rank Entities with Multi-Criteria Decision Making Methods(MCDM)

You can’t rest on your #1 ranking-because the guy at #2 isn’t resting. He’s still improving his site — Ryan Jones

We all come across different multi-criteria decision-making problems in our day to day life. Example — Shopping: Which one product should I buy out of X candidate products?

Ranking problems are the most interesting problems a data scientist gets to solve. Like such, I recently came across a ranking problem where we wanted to rank users and pick top K which are most beneficial for our business. To this problem, there is also a catch that right now I have no data to work on meaning this is a cold start problem where data will flow in with time.

Knowing the fact that I have zero training data points, I was sure there would be a better way to handle a ranking problem with multiple-criteria and came across this interesting publication “Triantaphyllou, E. (2000). Multi-criteria decision-making methods. In Multi-criteria decision making methods: A comparative study (pp. 5–21). Springer, Boston, MA.” which teaches about Multi-Criteria Decision Making Methods(MCDM).

ABSTRACT

Multiple criteria decision-making (MCDM) or Multi-criteria decision analysis (MCDA) is considered as a complex decision-making (DM) tool involving both quantitative and qualitative factors.

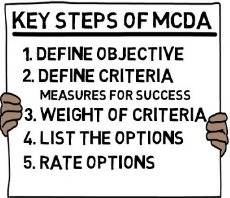
INTRODUCTION

After defining the first four key steps (image above) of Multi-Criteria Decision Making Methods(MCDM), in step 5 we process the numerical values to determine a ranking of each alternative.

To do this processing and ranking of different entities with multi-criteria we can use the following algorithms: WSM, WPM, AHP, revised AHP, ELECTRE, TOPSIS, and MOORA methods.

I. Weighted Sum Method

This is the simplest and most commonly used of all. We all have seen this in our school/college report cards too where the objective is to find:
Which student ranked first in a class?
Criteria are defined as — different subjects of a student
Weights of criteria — are credit scores assigned to a particular subject.

WSM Formula —

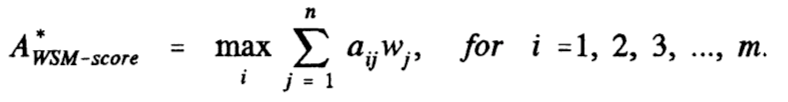
where: A*_WSM-score is the WSM score of the best alternative, n is the number of decision criteria, a_ij is the actual value of the i_th alternative in terms of the j^th criterion, and W_j is the weight of importance of the j^th criterion.

NOTE: It is very important to state here that WSM is applicable only when all the data are expressed in exactly the same unit (like in report card marks). If this is not the case, then the final result is equivalent to “adding apples and oranges.”

II. Weighted Product Method

WPM is very similar to above WSM, the main difference is that instead of adding in the model there is multiplication.

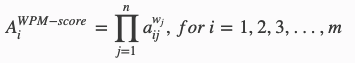
One may face the problem of INT Overflow as we are doing multiplication of exponential numbers to handle that use this modification (adding logarithm)to the original formula:

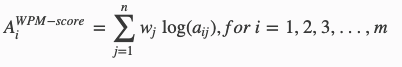
NOTE: WPM only gives alternatives performance value, not the relative ones i.e. we here are doing the pointwise ranking.

III. Analytic hierarchy process (AHP — Method)

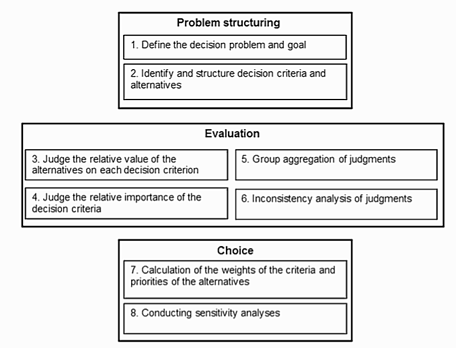
In the AHP method, we do a pairwise comparison between different alternatives and then rank them.

AHP method was release two times, the first version [Saaty, 1980] stated to normalize the alternate matrix in such a way that the relative values for each criterion sum up to one.

Then this AHP method was revised by Belton and Gear [1983] who proved that the relative values for each criterion sum up to one is causing ranking inconsistency. Instead of having the relative values of the alternatives A1, A2, A3, …, Am sum up to one, they proposed to divide each relative value by the maximum value of the relative values.

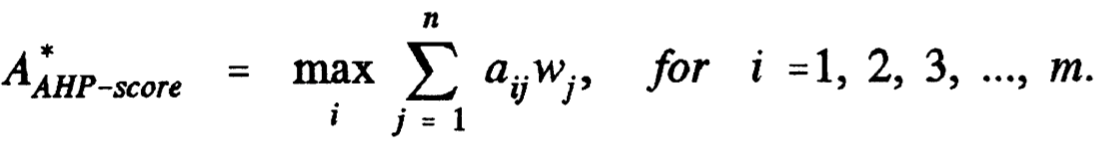
The similarity between the WSM and the AHP is clear. The AHP uses relative values instead of actual ones. Thus, it can be used in single- or multi-dimensional decision-making problems.

Proof — Of why AHP was revised?

Method1 — States that the relative values for each criterion sum up to one.

After Normalization by Method1

AHP Score — (0.45, 0.47, 0.08) → A2>A1>A3

On the above matrix, we introduce a new alternative, say A4, which is identical to A2 (i.e., A2 == A4)

AHP Score —(0.37, 0.29, 0.06, 0.29)→ A1>A2=A4>A3

This creates ranking inconsistency, as earlier (before A4 introduction) we stated A2>A1 and A4 being identical to A2 the ranking should not change.

Method2 — proposed to divide each relative value by the maximum value of the relative values.

After Normalization by Method2.

AHP Score (2/3, 19/27, 1/9, 19/27) → A2=A4>A1>A3.

Method2 of AHP solved the problem of ranking inconsistency but many researchers challenged that identical alternatives should not be considered in the decision process.

LET’S SOLVE A PROBLEM WITH WHATEVER WE HAVE LEARNED SO FAR

I wanted to buy a new mobile phone. So I spend 2–3 hours on Amazon after which I was able to shortlist 5 best smartphones. I was very confused about which phone will be the best value for the money of these 5. So, I followed our learned MCDM techniques —

• Let’s constructed an Alternate Matrix and Defined Criteria on which we will judge a smartphone.
• Best Phone is one with criteria as [Price, Storage, Camera, Looks] → [MIN, MAX, MAX, MAX]
• After some thinking about my needs added weightage to each criterion. [Price, Storage, Camera, Looks] → [0.4, 0.2, 0.3, 0.1] (Note: Sum of all weights such be equal to 1)

• Now, we need to normalize the alternate matrix (using Formula Below). In our phone selection problem, price is a non-beneficial attribute, and [Storage, Camera, Looks] are beneficial attributes.

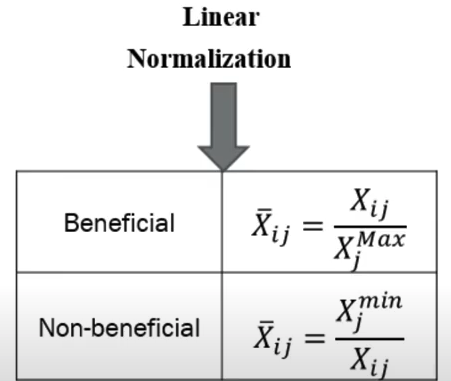
• Normalized Alternate Matrix — [Note: Now the best of the non-beneficial attribute is denoted as 1 and the best of the beneficial attribute is also denoted as 1.]

• Applying Weight Sum Method on this normalized matrix to get ranking—

• Applying Weighted Product Method on this normalized matrix to get ranking—

WSM, WPM, and AHP Methods are simple, fast in the calculation, and easily adjust to fit many sized problems; not data intensive.

About the Author

Shaurya Uppal

Shaurya Uppal is a Data Science enthusiast, who has worked on multiple data science problems in NLP, Ranking Algorithms, and Recommendation Engine. He has also published research papers in different IEEE conferences. He has a good sense of production, data problems, and can ameliorate business metrics.

LinkedIn: https://www.linkedin.com/in/shaurya-uppal/
Github: https://github.com/shauryauppal
StackOverFlow: https://stackoverflow.com/users/6897603/shaurya-uppal
Research Paper: https://scholar.google.co.in/citations?user=zNkN29oAAAAJ&hl=en