Interview Prep
Career
GenAI
Prompt Engg
ChatGPT
LLM
Langchain
RAG
AI Agents
Machine Learning
Deep Learning
GenAI Tools
LLMOps
Python
NLP
SQL
AIML Projects

Reading list

Machine Learning Basics for a Newbie
6 Steps of Machine learning Lifecycle Introduction to Predictive Modeling
Introduction to Exploratory Data Analysis & Data Insights Descriptive Statistics Inferential Statistics How to Understand Population Distributions?
Reading Data Files into Python Different Variable Datatypes
Probability for Data Science Basic Concepts of Probability Axioms of Probability Conditional Probability
Central Tendencies for Continuous Variables Spread of Data KDE plots for Continuous Variable Overview of Distribution for Continuous variables Normal Distribution Skewed Distribution Skeweness and Kurtosis Distribution for Continuous Variable
Central Tendencies for Categorical Variables Understanding Discrete Distributions Performing EDA on Categorical Variables
Dealing with Missing Values Understanding Outliers Identifying Outliers in Data Outlier Detection in Python Outliers Detection Using IQR, Z-score, LOF and DBSCAN
Sample and Population Central Limit Theorem Confidence Interval and Margin of Error
Bivariate Analysis Introduction
Covariance Pearson Correlation Spearman's Correlation & Kendall's Tau Correlation versus Causation Tabular and Graphical methods for Bivariate Analysis Performing Bivariate Analysis on Continuous-Continuous Variables
Tabular and Graphical methods for Continuous-Categorical Variables Introduction to Hypothesis Testing P-value Two sample Z-test T-test T-test vs Z-test Performing Bivariate Analysis on Continuous-Catagorical variables
Chi-Squares Test Bivariate Analysis on Categorical Categorical Variables
Multivariate Analysis A Comprehensive Guide to Data Exploration The Data Science behind IPL
Supervised Learning vs Unsupervised Learning Reinforcement Learning Generative and Descriminative Models Parametric and Non Parametric model
Machine Learning Pipeline Preparing Dataset Build a Benchmark Model: Regression Build a Benchmark Model: Classification
Evaluation Metrics for Machine Learning Everyone should know Confusion Matrix Accuracy Precision and Recall AUC-ROC Log Loss R2 and Adjusted R2
Dealing with Missing Values Replacing Missing Values Imputing Missing Values in Data Working with Categorical Variables Working with Outliers Preprocessing Data for Model Building
Understanding Cost Function Understanding Gradient Descent Math Behind Gradient Descent Assumptions of Linear Regression Implement Linear Regression from Scratch Train Linear Regression in Python Implementing Linear Regression in R Diagnosing Residual Plots in Linear Regression Models Generalized Linear Models Introduction to Logistic Regression Odds Ratio Implementing Logistic Regression from Scratch Introduction to Scikit-learn in Python Train Logistic Regression in python Multiclass using Logistic Regression How to use Multinomial and Ordinal Logistic Regression in R ? Challenges with Linear Regression Introduction to Regularisation Implementing Regularisation Ridge Regression Lasso Regression
Introduction to K Nearest Neighbours Determining the Right Value of K in KNN Implement KNN from Scratch Implement KNN in Python
Bias Variance Tradeoff Introduction to Overfitting and Underfitting Visualizing Overfitting and Underfitting Selecting the Right Model What is Validation? Hold-Out Validation Understanding K Fold Cross Validation
Introduction to Feature Selection Feature Selection Algorithms Missing Value Ratio Low Variance Filter High Correlation Filter Backward Feature Elimination Forward Feature Selection Implement Feature Selection in Python Implement Feature Selection in R
Introduction to Decision Tree Purity in Decision Tree Terminologies Related to Decision Tree How to Select Best Split Point in Decision Tree? Chi-Squares Information Gain Reduction in Variance Optimizing Performance of Decision Tree Train Decision Tree using Scikit Learn Pruning of Decision Trees
Introduction to Feature Engineering Feature Transformation Feature Scaling Feature Engineering Frequency Encoding Automated Feature Engineering: Feature Tools
Introduction to Naive Bayes Conditional Probability and Bayes Theorem Introduction to Bayesian Adjustment Rating: The Incredible Concept Behind Online Ratings! Working of Naive Bayes Math behind Naive Bayes Types of Naive Bayes Implementation of Naive Bayes
Understanding how to solve Multiclass and Multilabled Classification Problem Evaluation Metrics: Multi Class Classification
Introduction to Ensemble Techniques Basic Ensemble Techniques Implementing Basic Ensemble Techniques Finding Optimal Weights of Ensemble Learner using Neural Network Why Ensemble Models Work well?
Introduction to Stacking Implementing Stacking Variants of Stacking Implementing Variants of Stacking Introduction to Blending Bootstrap Sampling Introduction to Random Sampling Hyper-parameters of Random Forest Implementing Random Forest Out-of-Bag (OOB) Score in the Random Forest IPL Team Win Prediction Project Using Machine Learning Introduction to Boosting Gradient Boosting Algorithm Math behind GBM Implementing GBM in python Regularized Greedy Forests Extreme Gradient Boosting Implementing XGBM in python Tuning Hyperparameters of XGBoost in Python Implement XGBM in R/H2O Adaptive Boosting Implementing Adaptive Boosing LightGBM Implementing LightGBM in Python Catboost Implementing Catboost in Python
Different Hyperparameter Tuning methods Implementing Different Hyperparameter Tuning methods GridsearchCV RandomizedsearchCV Bayesian Optimization for Hyperparameter Tuning Hyperopt
Understanding SVM Algorithm SVM Kernels In-depth Intuition and Practical Implementation SVM Kernel Tricks Kernels and Hyperparameters in SVM Implementing SVM from Scratch in Python and R
Introduction to Principal Component Analysis Steps to Perform Principal Compound Analysis Computation of Covariance Matrix Finding Eigenvectors and Eigenvalues Implementing PCA in python Visualizing PCA A Brief Introduction to Linear Discriminant Analysis Introduction to Factor Analysis
Introduction to Clustering Applications of Clustering Evaluation Metrics for Clustering Understanding K-Means Implementation of K-Means in Python Implementation of K-Means in R Choosing Right Value for K Profiling Market Segments using K-Means Clustering Hierarchical Clustering Implementation of Hierarchial Clustering DBSCAN Defining Similarity between clusters Build Better and Accurate Clusters with Gaussian Mixture Models
Understand Basics of Recommendation Engine with Case Study
8 Ways to Improve Accuracy of Machine Learning Models
Introduction to Dask Working with CuML
Introduction to Machine Learning Interpretability Framework and Interpretable Models model Agnostic Methods for Interpretability Implementing Interpretable Model Understanding SHAP Out-of-Core ML Introduction to Interpretable Machine Learning Models Model Agnostic Methods for Interpretability Game Theory & Shapley Values
Introduction to Machine Learning Interpretability Framework and Interpretable Models model Agnostic Methods for Interpretability Implementing Interpretable Model Understanding SHAP Out-of-Core ML Introduction to Interpretable Machine Learning Models Model Agnostic Methods for Interpretability Game Theory & Shapley Values
Introduction to AutoML Implementation of MLBox Introduction to PyCaret TPOT Auto-Sklearn EvalML
Pickle and Joblib Introduction to Model Deployment
Deploying Machine Learning Model using Streamlit Deploying ML Models in Docker Deploy Using Streamlit Deploy on Heroku Deploy Using Netlify Introduction to Amazon Sagemaker Setting up Amazon SageMaker Using SageMaker Endpoint to Generate Inference Deploy on Microsoft Azure Cloud Introduction to Flask for Model Deploying ML model using Flask
Model Deployment in Android Model Deployment in Iphone

Confusion Matrix Is No More A Confusion for Data Science Aspirants!

RASHMI
RASHMI Last Updated : 05 Oct, 2020
5 min read

This article was published as a part of the Data Science Blogathon.

Introduction

After we have trained our model and have predicted the outcomes, we need to evaluate the model’s performance. And here comes our Confusion Matrix. But before diving into what is a confusion matrix and how it evaluates the model’s performance, let’s have a look into the picture below.

Confusion Matrix

What is the Confusion Matrix?

It is the 2-dimensional array representation of the above table.

Confusion Matrix

The above 2-dimensional array is the Confusion Matrix which evaluates the performance of a classification model on a set of predicted values for which the true(or actual) values are known. 

 

Terminologies

Let’s have a definition of the four important terms that define the confusion matrix-

True Positive:

Cases, where the model claims that something has happened and actually it has happened i.e patient, has cancer and the model also predicts cancer.

True Negative:

Cases, where the model claims that nothing has happened and actually nothing, has happened i.e patient doesn’t have cancer and the model also doesn’t predict cancer.

False Positive ( Type-1 error):

Cases, where the model claims that something has happened when actually it hasn’t i.e patient, doesn’t have cancer but the model predicts cancer.

False Negative (Type-2 error):

Cases,  where the model claims nothing when actually something has happened i.e patient has cancer but the model doesn’t predict cancer.

 

How does the Confusion Matrix evaluate the model’s performance?

Now, all we need to know is how this matrix works on the dataset. For this, I’ll be using the same above case but in the form of a dataset.

     Feature 1       Feature 2         . . . . .             Target
( has cancer: 0,
doesn’t have cancer:1)		        Prediction
( what our model predicted)
                  1                 1
                  0                 1
                  1                 1
                  1                 0
                  0                 0
                  0                 0
                  1                 1
                  1                 1
                  0                 0

In the above classification dataset, Feature 1, Feature 2, and up to Feature n are the independent variables. For Target (dependent variable) we have assigned 1 to a positive value (i.e have cancer) and 0 to a negative value (i.e doesn’t have cancer). After we have trained our model and got our predictions and we want to evaluate the performance, this is how the confusion matrix would look like.

Confusion Matrix
  • TP = 4, There are four cases in the dataset where the model predicted 1 and the target was also 1
  • FP = 1, There is only one case in the dataset where the model predicted 1 but the target was 0
  • FN = 1, There is only one case in the dataset where the model predicted 0 but the target was 1
  • TN = 3, There are three cases in the dataset where the model predicted 0 and the target was also 0

Why is the Confusion Matrix important?

The below-given metrics of confusion matrix determine how well our model performs-

  1. Accuracy
  2. Precision (Positive Prediction Value)
  3. Recall (True Positive Rate or Sensitivity)
  4. F beta Score

 

1. ACCURACY:

Accuracy is the number of correctly (True) predicted results out of the total.

                                                   Accuracy = (TP + TN) / (TP + TN + FP + FN)

= (4 + 3) / 9 = 0.77

Accuracy should be considered when TP and TN are more important and the dataset is balanced because in that case the model will not get baised based on the class distribution. But in real-life classification problem, imbalanced class distribution exists.

For example, we have an imbalanced test data with 900 records of positive class (1) and 100 records of negative class (0). And our model predicted all records as positive (1). In that scenario, TP will be 900 and TN will be 0. Thus, accuracy = (900 + 0) / 1000 = 90%

Therefore, we should consider Precision, Recall and F Score as a better metric to evaluate the model.

 

2. PRECISION:

Out of the total predicted positive values, how many were actually positive

                                                Precision = TP / (TP + FP) = 4/5 = 0.8

 

When precision should be considered?

Taking a use case of Spam Detection, suppose the mail is not spam (0), but the model has predicted it as spam (1) which is FP. In this scenario, one can miss the important mail. So, here we should focus on reducing the FP and must consider precision in this case.

 

3. RECALL:

Out of the total actual positive values, how many were correctly predicted as positive

                                                     Recall= TP / (TP + FN) = 4/5 = 0.8

 

When recall should be considered?

In Cancer Detection, suppose if a person is having cancer (1), but it is not predicted (0) by the model which is FN. This could be a disaster. So, in this scenario, we should focus on reducing the FN and must consider recall in this case.

 

Based on the problem statement, whenever the FP is having a greater impact, go for Precision and whenever the FN is important, go for Recall

 

4. F beta SCORE

In some use cases, both precision and recall are important. Also, in some use cases even though precision plays an important role or recall plays is important, we should combine both to get the most accurate result.

.

Selecting beta value

F-1 Score (beta =1 )

When FP and FN both are equally important. This allows the model to consider both precision and recall equally using a single score.

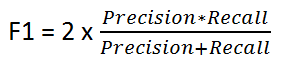
Image for post

F-1 Score is the Harmonic Mean of precision and recall.

 

Smaller beta value such as (beta = 0.5).

If the impact of FP is high. This will give more weight to precision than to recall.

 

Higher beta value such (beta = 2)

If the impact of FN is high. Thus, giving more weight to recall and less to precision.

Hope you found this useful and interesting.

RASHMI
RASHMI

Free Courses

Generative AI 4.7

Generative AI - A Way of Life

Explore Generative AI for beginners: create text and images, use top AI tools, learn practical skills, and ethics.
Large Language Models 4.5

Getting Started with Large Language Models

Master Large Language Models (LLMs) with this course, offering clear guidance in NLP and model training made simple.
Prompt Engineering 4.6

Building LLM Applications using Prompt Engineering

This free course guides you on building LLM apps, mastering prompt engineering, and developing chatbots with enterprise data.
LlamaIndex 4.8

Improving Real World RAG Systems: Key Challenges & Practical Solutions

Explore practical solutions, advanced retrieval strategies, and agentic RAG systems to improve context, relevance, and accuracy in AI-driven applications.
RAG systems using LlamaIndex 4.7

Microsoft Excel: Formulas & Functions

Master MS Excel for data analysis with key formulas, functions, and LookUp tools in this comprehensive course.

Recommended Articles

Responses From Readers

Clear

Prajwal KV
Prajwal KV

Great article.clearly explained. There is a mistake in the recall paragraph. When recall should be considered? In Cancer Detection, suppose if a person is having cancer (1), but it is not ('not' should not be here)predicted (0) by the model which is FN. This could be a disaster. So, in this scenario, we should focus on reducing the FN and must consider recall in this case.

123

Charvik
Charvik

Great article. Very informative and great explanation.

123

Write for us

Write, captivate, and earn accolades and rewards for your work
  • Reach a Global Audience
  • Get Expert Feedback
  • Build Your Brand & Audience
  • Cash In on Your Knowledge
  • Join a Thriving Community
  • Level Up Your Data Science Game
imag

We use cookies essential for this site to function well. Please click to help us improve its usefulness with additional cookies. Learn about our use of cookies in our Privacy Policy & Cookies Policy.

Show details