Interview Prep
Career
GenAI
Prompt Engg
ChatGPT
LLM
Langchain
RAG
AI Agents
Machine Learning
Deep Learning
GenAI Tools
LLMOps
Python
NLP
SQL
AIML Projects

Reading list

Machine Learning Basics for a Newbie
6 Steps of Machine learning Lifecycle Introduction to Predictive Modeling
Introduction to Exploratory Data Analysis & Data Insights Descriptive Statistics Inferential Statistics How to Understand Population Distributions?
Reading Data Files into Python Different Variable Datatypes
Probability for Data Science Basic Concepts of Probability Axioms of Probability Conditional Probability
Central Tendencies for Continuous Variables Spread of Data KDE plots for Continuous Variable Overview of Distribution for Continuous variables Normal Distribution Skewed Distribution Skeweness and Kurtosis Distribution for Continuous Variable
Central Tendencies for Categorical Variables Understanding Discrete Distributions Performing EDA on Categorical Variables
Dealing with Missing Values Understanding Outliers Identifying Outliers in Data Outlier Detection in Python Outliers Detection Using IQR, Z-score, LOF and DBSCAN
Sample and Population Central Limit Theorem Confidence Interval and Margin of Error
Bivariate Analysis Introduction
Covariance Pearson Correlation Spearman's Correlation & Kendall's Tau Correlation versus Causation Tabular and Graphical methods for Bivariate Analysis Performing Bivariate Analysis on Continuous-Continuous Variables
Tabular and Graphical methods for Continuous-Categorical Variables Introduction to Hypothesis Testing P-value Two sample Z-test T-test T-test vs Z-test Performing Bivariate Analysis on Continuous-Catagorical variables
Chi-Squares Test Bivariate Analysis on Categorical Categorical Variables
Multivariate Analysis A Comprehensive Guide to Data Exploration The Data Science behind IPL
Supervised Learning vs Unsupervised Learning Reinforcement Learning Generative and Descriminative Models Parametric and Non Parametric model
Machine Learning Pipeline Preparing Dataset Build a Benchmark Model: Regression Build a Benchmark Model: Classification
Evaluation Metrics for Machine Learning Everyone should know Confusion Matrix Accuracy Precision and Recall AUC-ROC Log Loss R2 and Adjusted R2
Dealing with Missing Values Replacing Missing Values Imputing Missing Values in Data Working with Categorical Variables Working with Outliers Preprocessing Data for Model Building
Understanding Cost Function Understanding Gradient Descent Math Behind Gradient Descent Assumptions of Linear Regression Implement Linear Regression from Scratch Train Linear Regression in Python Implementing Linear Regression in R Diagnosing Residual Plots in Linear Regression Models Generalized Linear Models Introduction to Logistic Regression Odds Ratio Implementing Logistic Regression from Scratch Introduction to Scikit-learn in Python Train Logistic Regression in python Multiclass using Logistic Regression How to use Multinomial and Ordinal Logistic Regression in R ? Challenges with Linear Regression Introduction to Regularisation Implementing Regularisation Ridge Regression Lasso Regression
Introduction to K Nearest Neighbours Determining the Right Value of K in KNN Implement KNN from Scratch Implement KNN in Python
Bias Variance Tradeoff Introduction to Overfitting and Underfitting Visualizing Overfitting and Underfitting Selecting the Right Model What is Validation? Hold-Out Validation Understanding K Fold Cross Validation
Introduction to Feature Selection Feature Selection Algorithms Missing Value Ratio Low Variance Filter High Correlation Filter Backward Feature Elimination Forward Feature Selection Implement Feature Selection in Python Implement Feature Selection in R
Introduction to Decision Tree Purity in Decision Tree Terminologies Related to Decision Tree How to Select Best Split Point in Decision Tree? Chi-Squares Information Gain Reduction in Variance Optimizing Performance of Decision Tree Train Decision Tree using Scikit Learn Pruning of Decision Trees
Introduction to Feature Engineering Feature Transformation Feature Scaling Feature Engineering Frequency Encoding Automated Feature Engineering: Feature Tools
Introduction to Naive Bayes Conditional Probability and Bayes Theorem Introduction to Bayesian Adjustment Rating: The Incredible Concept Behind Online Ratings! Working of Naive Bayes Math behind Naive Bayes Types of Naive Bayes Implementation of Naive Bayes
Understanding how to solve Multiclass and Multilabled Classification Problem Evaluation Metrics: Multi Class Classification
Introduction to Ensemble Techniques Basic Ensemble Techniques Implementing Basic Ensemble Techniques Finding Optimal Weights of Ensemble Learner using Neural Network Why Ensemble Models Work well?
Introduction to Stacking Implementing Stacking Variants of Stacking Implementing Variants of Stacking Introduction to Blending Bootstrap Sampling Introduction to Random Sampling Hyper-parameters of Random Forest Implementing Random Forest Out-of-Bag (OOB) Score in the Random Forest IPL Team Win Prediction Project Using Machine Learning Introduction to Boosting Gradient Boosting Algorithm Math behind GBM Implementing GBM in python Regularized Greedy Forests Extreme Gradient Boosting Implementing XGBM in python Tuning Hyperparameters of XGBoost in Python Implement XGBM in R/H2O Adaptive Boosting Implementing Adaptive Boosing LightGBM Implementing LightGBM in Python Catboost Implementing Catboost in Python
Different Hyperparameter Tuning methods Implementing Different Hyperparameter Tuning methods GridsearchCV RandomizedsearchCV Bayesian Optimization for Hyperparameter Tuning Hyperopt
Understanding SVM Algorithm SVM Kernels In-depth Intuition and Practical Implementation SVM Kernel Tricks Kernels and Hyperparameters in SVM Implementing SVM from Scratch in Python and R
Introduction to Principal Component Analysis Steps to Perform Principal Compound Analysis Computation of Covariance Matrix Finding Eigenvectors and Eigenvalues Implementing PCA in python Visualizing PCA A Brief Introduction to Linear Discriminant Analysis Introduction to Factor Analysis
Introduction to Clustering Applications of Clustering Evaluation Metrics for Clustering Understanding K-Means Implementation of K-Means in Python Implementation of K-Means in R Choosing Right Value for K Profiling Market Segments using K-Means Clustering Hierarchical Clustering Implementation of Hierarchial Clustering DBSCAN Defining Similarity between clusters Build Better and Accurate Clusters with Gaussian Mixture Models
Understand Basics of Recommendation Engine with Case Study
8 Ways to Improve Accuracy of Machine Learning Models
Introduction to Dask Working with CuML
Introduction to Machine Learning Interpretability Framework and Interpretable Models model Agnostic Methods for Interpretability Implementing Interpretable Model Understanding SHAP Out-of-Core ML Introduction to Interpretable Machine Learning Models Model Agnostic Methods for Interpretability Game Theory & Shapley Values
Introduction to Machine Learning Interpretability Framework and Interpretable Models model Agnostic Methods for Interpretability Implementing Interpretable Model Understanding SHAP Out-of-Core ML Introduction to Interpretable Machine Learning Models Model Agnostic Methods for Interpretability Game Theory & Shapley Values
Introduction to AutoML Implementation of MLBox Introduction to PyCaret TPOT Auto-Sklearn EvalML
Pickle and Joblib Introduction to Model Deployment
Deploying Machine Learning Model using Streamlit Deploying ML Models in Docker Deploy Using Streamlit Deploy on Heroku Deploy Using Netlify Introduction to Amazon Sagemaker Setting up Amazon SageMaker Using SageMaker Endpoint to Generate Inference Deploy on Microsoft Azure Cloud Introduction to Flask for Model Deploying ML model using Flask
Model Deployment in Android Model Deployment in Iphone

Statistics and Probability Concepts for Data Science

M
Manasvi Last Updated : 14 Oct, 2024
7 min read

Introduction

As far as data science is concerned, basic statistics & probability goes long way. These are two sciences which provide the basis for all data analysis; they allow us to understand, play with and generally utilise some incredibly large pools of information. From understanding patterns to making data-driven decision or building sophisticated machine learning models, there is no other way but the concepts of statistics and probability. In this blog, we will be discussing some very fundamental concepts like Types of data, Mean, Median, Mode,Variability — Variance and Standard deviation plus Probability as well which is considered so much important for any aspirating Data Scientist.

Statistics is the grammar of Science.
– Karl Pearson

This article was published as a part of the Data Science Blogathon.

Table of contents

What is Data?

Statistics and Probability data | what is data in statistics

Image Credits

Data is the information collected through different sources which can be qualitative or quantitative in nature. Mostly, the data collected is used to analyze and draw insights on a particular topic.

For example:

  1. Cylinder size, mileage, color, etc. for the sale of a car
  2. If the cells in the body are malignant or benign to detect Cancer

Types of Data

Types of Data | what is data in statistics

Numerical Data

Numerical data is the information in numbers i.e. numeric which poses as a quantitative measurement of things.

For example:

  1. Heights and weights of people
  2. Stock Prices

a) Discrete Data

Discrete data is the information that often counts of some event i.e. can only take specific values. These are often integer-based, but not necessarily.

For example:

  1. Number of times a coin was flipped
  2. Shoe sizes of people

b) Continuous Data

Continuous Data is the information that has the possibility of having infinite values i.e. can take any value within a range.

For example:

How many centimeters of rain fell on a given day

Categorical Data

This type of data is qualitative in nature which has no inherent mathematical significance. It is sort of a fixed value under which a unit of observation is assigned or “categorized”.

For example:

  1. Gender
  2. Binary Data (Yes/No)
  3. Attributes of a vehicle like color, mileage, number of doors, etc.

Ordinal Data

This type of data is the combination of numerical and categorical data i.e. categorical data having some mathematical significance.

For example:

Restaurant ratings from 1-5, 1 being the lowest and 5 being the highest

Mean, Median and Mode

Mean

In mathematics and statistics, the mean is the average of the numerical observations which is equal to the sum of the observations divided by the number of observations.

A= frac {1}{n} sum limits_{i=1}^n a_i mean Statistics and Probability

where,

A=arithmetic mean
n=number of values
a_i=data set values

Median

The median of the data, when arranged in ascending or descending value is the middle observation of the data i.e. the point separating the higher half to the lower half of the data.

To calculate the median:

  • Arrange the data in ascending or descending order.
  • an odd number of data points: the middle value is the median.
  • even number of data points: the average of the two middle values is the median.
median Statistics and Probability
X=an ordered list of values in the data set
n=number of values in data set

Mode

The mode of a set of data points is the most frequently occurring value.

For example:

5,2,6,5,1,1,2,5,3,8,5,9,5 are the set of data points. Here 5 is the mode because it’s occurring most frequently.

Variance and Standard Deviation

Variance

Mathematically and statistically, variance is defined as the average of the squared differences from the mean. But for understanding, this depicts how spread out the data is in a dataset.

The steps of calculating variance using an example:

Let’s find the variance of (1,4,5,4,8)

  1. Find the mean of the data points i.e. (1 + 4 + 5 + 4 + 8)/5 = 4.4
  2. Find the differences from the mean i.e. (-3.4, -0.4, 0.6, -0.4, 3.6)
  3. Find the squared differences i.e. (11.56, 0.16, 0.36, 0.16, 12.96)
  4. Find the average of the squared differences i.e. 11.56+0.16+0.36+0.16+12.96/5=5.04

The formula for the same is:

Statistics and Probability variance

Standard Deviation

Standard deviation measures the variation or dispersion of the data points in a dataset. It depicts the closeness of the data point to the mean and is calculated as the square root of the variance.

In data science, the standard deviation is usually used to identify the outliers in a data set. The data points which lie one standard deviation away from the mean are considered to be unusual.

The formula for standard deviation is:

Statistics and Probability standard deviation | what is data in statistics
sigma=population standard deviation
N=the size of the population
x_i=each value from the population
mu=the population mean

Population Data V/s Sample Data

Population data refers to the complete data set whereas sample data refers to a part of the population data which is used for analysis. Sampling is done to make analysis easier.

When using sample data for analysis, the formula of variance is slightly different. If there are total n samples we divide by n-1 instead of n:

Statistics and Probability population data
S^2=sample variance
x_i=the value of the one observation
bar{x}=the mean value of observations
n=the number of observations

Probability

Probability | what is data in statistics

Image Credits

What is Probability?

The concept of probability is extremely simple. It means how likely an event is about to occur or the chance of the occurrence of an event.

The  formula for probability is:

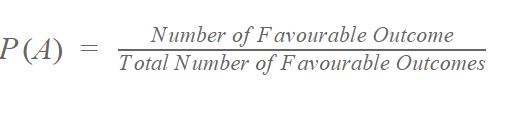
Probability Formulas- List of Basic Probability Formulas With Examples

For example:

The probability of the coin showing heads when it’s flipped is 0.5.

Conditional Probability

Conditional probability is the probability of an event occurring provided another event has already occurred.

The formula of conditional probability:

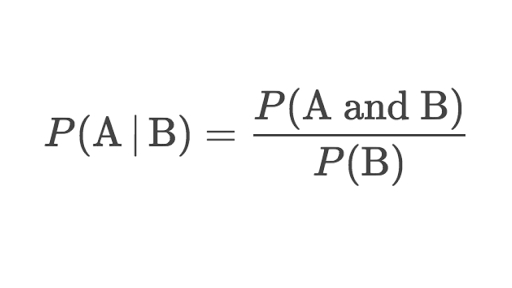
Conditional probability using two-way tables (article) | Khan Academy

For example:

The students of a class have given two tests of the subject mathematics. In the first test, 60% of the students pass while only 40% of the students passed both the tests. What percentage of students who passed the first test, cleared the second test?

conditional probability example | what is data in statistics

Bayes’ Theorem

Bayes’ Theorem is a very important statistical concept used in many industries such as healthcare and finance. The formula of conditional probability which we have done above has also been derived from this theorem.

It is used to calculate the probability of a hypothesis based on the probabilities of various data provided in the hypothesis.

The formula for Bayes’ theorem is:

bayes theorem
A, B=events
P(A|B)=probability of A given B is true
P(B|A)=probability of B given A is true
P(A), P(B)=the independent probabilities of A and B

For example:

Let’s assume there is an HIV test that can identify HIV+ positive patients accurately 99% of the time, and also accurately has a negative result for 99% of HIV negative people. Here, only 0.3% of the overall population is HIV positive.

bayes theorem

Conclusion

The topics of statistics and probability covered in the article are really important but there are many other topics such as Probability Distribution Functions and their types, Covariance, and Correlation, etc. that have not been covered here because they require separate attention due to their graphical nature.

Mathematics and statistics are the heart of data science. The topics covered in this article are the basis of many algorithms, error calculating formulas, and graphical understanding of things, thus are very important and cannot be ignored.

blogathondata scienceprobabilitystatisticsStatistics and Probabilitystatistics and probability for data sciencewhat is data in statistics
M
Manasvi

Free Courses

Generative AI 4.7

Generative AI - A Way of Life

Explore Generative AI for beginners: create text and images, use top AI tools, learn practical skills, and ethics.
Large Language Models 4.5

Getting Started with Large Language Models

Master Large Language Models (LLMs) with this course, offering clear guidance in NLP and model training made simple.
Prompt Engineering 4.6

Building LLM Applications using Prompt Engineering

This free course guides you on building LLM apps, mastering prompt engineering, and developing chatbots with enterprise data.
LlamaIndex 4.8

Improving Real World RAG Systems: Key Challenges & Practical Solutions

Explore practical solutions, advanced retrieval strategies, and agentic RAG systems to improve context, relevance, and accuracy in AI-driven applications.
RAG systems using LlamaIndex 4.7

Microsoft Excel: Formulas & Functions

Master MS Excel for data analysis with key formulas, functions, and LookUp tools in this comprehensive course.

Recommended Articles

Responses From Readers

Clear

Ritu Malhotra
Ritu Malhotra

All the best Manasvi

123

Suchitra
Suchitra

A very well drafted analysis.

123

Brig RS Kochhar
Brig RS Kochhar

The concepts have been explained in a simplified manner and one can understand the basics from the paper. Well written.

123

Write for us

Write, captivate, and earn accolades and rewards for your work
  • Reach a Global Audience
  • Get Expert Feedback
  • Build Your Brand & Audience
  • Cash In on Your Knowledge
  • Join a Thriving Community
  • Level Up Your Data Science Game
imag
Congratulations, You Did It!
Well Done on Completing Your Learning Journey. Stay curious and keep exploring!
End to End Statistics for Data Science
End to End Statistics for Data Science
15 Basic Statistics Concepts Every Data Science Beginner Should Know
15 Basic Statistics Concepts Every Data Science Beginner Should Know

We use cookies essential for this site to function well. Please click to help us improve its usefulness with additional cookies. Learn about our use of cookies in our Privacy Policy & Cookies Policy.

Show details