Introduction
Starting with the construction of a neural network, even a basic one, can feel confusing. Improving its performance can be a lot of work. In deep neural networks, we often face a problem called “Vanishing and Exploding gradient descent.” This means the gradients become too small or too large during training, making learning difficult.
One solution to this problem is to carefully set the starting values for our network’s parameters. This process is called “Weight initialization.” Essentially, it’s about choosing the right starting points for the weights and biases in our neural network.
This discussion assumes you’re familiar with basic neural network concepts like weights, biases, and activation functions, as well as how forward and backward propagation work. We’ll be using Keras, a popular deep learning library in Python, to build our neural network. Our data will come from normal distributions, which are just ways of generating random numbers with a certain mean and variance.
Learning Outcomes
- Profound comprehension of the pivotal role of weight initialization in machine learning algorithms, particularly within artificial neural networks.
- Mastery of diverse weight initialization techniques, encompassing zero initialization, He-et-al, Xavier, and Kaiming, and their implications for model performance and convergence.
- Expertise in selecting appropriate weight initialization strategies to mitigate issues like vanishing or exploding gradients, ensuring robust learning dynamics in deep learning models.
- Fluency in fundamental training steps, including forward and backward propagation, loss computation, and gradient descent optimization, critical for effective model training.
- Advanced understanding of regularization techniques and their synergy with weight initialization for enhancing model generalization and preventing overfitting in diverse datasets.
This article was published as a part of the Data Science Blogathon.
Table of contents
Basics and Notations
Consider a neural network having an l layer, which has l-1 hidden layers and 1 output layer. Then, the parameters i.e, weights and biases of the layer l are represented as,

In addition to weights and biases, some more intermediate variables are also computed during the training process,
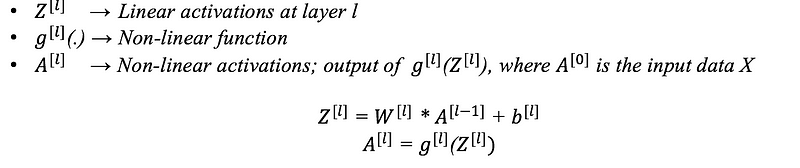
Steps of Training a Neural Network
Training a neural network consists of the following basic steps:
Step 1: Initialization of Neural Network
Initialize weights and biases.
Step 2: Forward propagation
Using the given input X, weights W, and biases b, for every layer we compute a linear combination of inputs and weights (Z)and then apply activation function to linear combination (A). At the final layer, we compute f(A(l-1)) which could be a sigmoid (for binary classification problem), softmax (for multi-class classification problem), and this gives the prediction y_hat.
Step 3: Compute the loss function
The loss function includes both the actual label y and predicted label y_hat in its expression. It shows how far our predictions from the actual target, and our main objective is to minimize the loss function.
Step 4: Backward Propagation
In backpropagation, we find the gradients of the loss function, which is a function of y and y_hat, and gradients wrt A, W, and b called dA, dW, and db. By using these gradients, we update the values of the parameters from the last layer to the first layer.
Step 5: Repetition
Repeat steps 2–4 for n epochs till we observe that the loss function is minimized, without overfitting the train data.
For Example, for a neural network having 2 layers, i.e. one hidden layer. (Here bias term is not added just for the simplicity)

Why Weight Initialization?
Its main objective is to prevent layer activation outputs from exploding or vanishing gradients during the forward propagation. If either of the problems occurs, loss gradients will either be too large or too small, and the network will take more time to converge if it is even able to do so at all.
If we initialized the weights correctly, then our objective i.e., optimization of loss function will be achieved in the least time otherwise converging to a minimum using gradient descent will be impossible.
Different Weight Initialization Techniques
One of the important things which we have to keep in mind while building your neural network is to initialize your weight matrix for different connections between layers correctly.
Let us see the following two initialization scenarios which can cause issues while we training the model:
Zero Initialization (Initialized all weights to 0)
If we initialized all the weights with 0, then what happens is that the derivative wrt loss function is the same for every weight in W[l], thus all weights have the same value in subsequent iterations. This makes hidden layers symmetric and this process continues for all the n iterations. Thus initialized weights with zero make your network no better than a linear model. It is important to note that setting biases to 0 will not create any problems as non-zero weights take care of breaking the symmetry and even if bias is 0, the values in every neuron will still be different.
Random Initialization (Initialized weights randomly)
This technique aims to tackle the issues associated with zero initialization by preventing neurons from learning identical features of their inputs. Given that the number of inputs significantly influences neural network behavior, our objective is to ensure that each neuron learns distinct functions of its input space. This approach yields superior accuracy compared to zero initialization, as it fosters greater diversity in feature representation learning. In general, it is used to break the symmetry. It is better to assign random values except 0 to weights.
Remember, neural networks are very sensitive and prone to overfitting as it quickly memorizes the training data.
Vanishing gradients
- For any activation function, abs(dW) will get smaller and smaller as we go backward with every layer during backpropagation especially in the case of deep neural networks. So, in this case, the earlier layers’ weights are adjusted slowly.
- Due to this, the weight update is minor which results in slower convergence.
- This makes the optimization of our loss function slow. It might be possible in the worst case, this may completely stop the neural network from training further.
- More specifically, in the case of the sigmoid and tanh and activation functions, if your weights are very large, then the gradient will be vanishingly small, effectively preventing the weights from changing their value. This is because abs(dW) will increase very slightly or possibly get smaller and smaller after the completion of every iteration.
- So, here comes the use of the RELU activation function in which vanishing gradients are generally not a problem as the gradient is 0 for negative (and zero) values of inputs and 1 for positive values of inputs.
Exploding gradients
- This is the exact opposite case of the vanishing gradients, which we discussed above.
- Consider we have weights that are non-negative, large, and having small activations A. When these weights are multiplied along with the different layers, they cause a very large change in the value of the overall gradient (cost). This means that the changes in W, given by the equation W= W — ⍺ * dW, will be in huge steps, the downward moment will increase.
Problems occurred due to exploding gradients
- This problem might result in the oscillation of the optimizer around the minima or even overshooting the optimum again and again and the model will never learn.
- Due to the large values of the gradients, it may cause numbers to overflow which results in incorrect computations or introductions of NaN’s (missing values).
Best Practices for Weight Initialization
Use RELU or leaky RELU as the activation function
As they both are relatively robust to the vanishing or exploding gradient problems (especially for networks that are not too deep). In the case of leaky RELU, they never have zero gradients. Thus they never die and training continues.
Use Heuristics for weight initialization
For deep neural networks, we can use any of the following heuristics to initialize the weights depending on the chosen non-linear activation function.
While these heuristics do not completely solve the exploding or vanishing gradients problems, they help to reduce it to a great extent. The most common heuristics are as follows:
(a) For RELU activation function: This heuristic is called He-et-al Initialization.
In this heuristic, we multiplied the randomly generated values of W by:
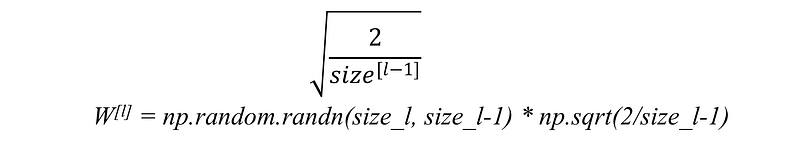
(b) For tanh activation function : This heuristic is known as Xavier initialization.
In this heuristic, we multiplied the randomly generated values of W by:
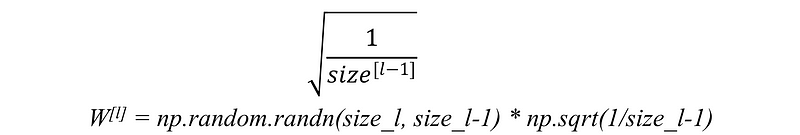
(c) Another commonly used heuristic is:

Benefits of Using These Heuristics
- All these heuristics serve as good starting points for weight initialization and they reduce the chances of exploding or vanishing gradients.
- All these heuristics do not vanish or explode too quickly, as the weights are neither too much bigger than 1 nor too much less than 1.
- They help to avoid slow convergence and ensure that we do not keep oscillating off the minima.
Note:
Gradient Clipping is another way for dealing with the exploding gradient problem. In this technique, we set a threshold value, and if our chosen function of a gradient is larger than this threshold, then we set it to another value.
In this article, we have talked about various initializations of weights, but not the biases since gradients wrt bias will depend only on the linear activation of that layer, but not depend on the gradients of the deeper layers. Thus, there is not a problem of diminishing or explosion of gradients for the bias terms. So, Biases can be safely initialized to 0.
Conclusion
In summary, this tutorial emphasizes the critical role of proper weight initialization in deep learning, especially within artificial neural networks. By exploring various initialization techniques, from zero to advanced methods like He-et-al and Xavier, we learn how initial values impact model performance. We also delve into training steps, highlighting the importance of forward and backward propagation, loss computation, and gradient descent. The tutorial extends to advanced topics like convolutional neural networks (CNNs), showcasing the broader applicability of weight initialization strategies. Ultimately, it equips practitioners with essential insights for effectively developing and optimizing deep learning models.
Key Take Away
- Weight initialization serves as a cornerstone in machine learning algorithms, influencing model performance and convergence across diverse datasets and scenarios.
- Various initialization techniques, such as He-et-al and Kaiming, offer tailored approaches to initializing network parameters, catering to different activation functions and architectures.
- TensorFlow and PyTorch frameworks provide robust support for implementing diverse weight initialization strategies seamlessly within deep learning models.
- Attention to regularization techniques, coupled with weight initialization, is vital for model generalization and preventing overfitting in machine learning applications.
- Understanding uniform distribution in weight initialization underscores the importance of maintaining balance and stability in model training dynamics.
Frequently Asked Questions
A. Weights and biases in neural networks are typically initialized randomly to break symmetry and prevent convergence to poor local minima. Weights are initialized from a random distribution such as uniform or normal, while biases are often initialized to zeros or small random values.
A. A good weight initialization technique should help prevent issues like vanishing or exploding gradients. Techniques like Xavier initialization (also known as Glorot initialization) and He initialization are commonly used.
A. In PyTorch, weights and biases can be initialized using functions provided by the torch.nn.init module. For example, the torch.nn.init.xavier_uniform_() function initializes weights using Xavier initialization with a uniform distribution, and torch.nn.init.zeros_() initializes biases to zeros.
A. In a Perceptron, weights are typically initialized randomly using a specified distribution, such as uniform or normal distribution. Biases are often initialized to zero or small random values.
The media shown in this article is not owned by Analytics Vidhya and is used at the Author’s discretion.








Hello, I have little note about your great article, next time, can you use other letter for number of layers? 'l' and '1' are quite simillar, and it's hard to read