K-Means: Getting the Optimal Number of Clusters

Introduction

In this beginner’s tutorial on data science, we will discuss determining the optimal number of clusters in a data set, which is a fundamental issue in partitioning clustering, such as k-means clustering. K-means clustering is an unsupervised learning machine learning algorithm. In an unsupervised algorithm, we are not interested in making predictions (since we don’t have a target/output variable). The objective is to discover interesting patterns in the data, e.g., are there any subgroups or ‘clusters’ among the bank’s customers?

Clustering techniques use raw data to form clusters based on common factors among various data points. Customer segmentation for targeted marketing is one of the most vital applications of the clustering algorithm. Also, in this article, you will learn that k means silhouette score.

Learning Objectives

• In this tutorial, we will learn about K-means clustering, an unsupervised machine-learning model, and its implementation in Python.
•  K-means is mostly used in customer insight, marketing, medical, and social media.
• Also, you will learn about the Silhouette Score Kmeans and Silhouette Analysis.

This article was published as a part of the Data Science Blogathon.

Practical Application of Clustering

Let us now look at some practical applications of clustering.

Customer Insight

A retail chain with many stores across locations wants to manage its stores effectively and increase sales and performance. Cluster analysis can help the retail chain gain insights on customer demographics, purchase behavior, and demand patterns across locations.

This will help the retail chain with assortment planning, promotional activities, and store benchmarking for better performance and higher returns.

Marketing

Cluster Analysis can be helpful in marketing. It can help with market segmentation and positioning and identify test markets for new product development.

As an online store manager, you would want to group the customers into different clusters so that you can create a customized marketing campaign for each group. You do not have any label in mind, such as ‘good customer’ or ‘bad customer.’ You want to just look at patterns in customer data and try to find segments. This is where clustering techniques can help.

Social Media

In social networking and social media, Cluster Analysis is used to identify similar communities within larger groups.

Medical

Researchers have widely used cluster analysis in biology and medical science for tasks such as sequencing into gene families, human genetic clustering, building groups of genes, clustering organisms at species, and so on.

Important Factors to Consider While Using the K-means Algorithm

Certain factors can impact the efficacy of the final clusters formed when using k-means clustering. So, we must consider the following factors when finding the optimal value of k. Solving business problems using the K-means clustering algorithm.

• Number of clusters (K): You must predefine the number of clusters into which you want to group your data points.
• Initial Values/ Seeds: The choice of the initial cluster centres can impact the final cluster formation. The K-means algorithm is non-deterministic, which means that the outcome of clustering can be different each time the algorithm is run, even on the same data set.
• Outliers: Cluster formation is very sensitive to the presence of outliers. Outliers pull the cluster towards itself, thus affecting optimal cluster formation.
• Distance Measures: Different distance measures (used to calculate the distance between a data point and cluster center) might yield different clusters.
• The K-Means algorithm does not work with categorical data.
• The process may not converge in the given number of iterations. You should always check for convergence.

How Does K-means Clustering Algorithm Work?

It will compute the squared Euclidean distance whenever the centroids move to measure the similarity between the samples and centroids. Hence, it works very well in identifying clusters with a spherical shape.

What is Silhouette Score K-Means?

The silhouette score interpretation measures the quality of k-means silhouette score by evaluating how well data points group within their assigned clusters compared to data points in other clusters.

Here’s a breakdown of the silhouette score for K-means:

Calculation:

The silhouette score is calculated for each data point and then averaged across all data points. It considers two distances for each data point:

• a: Average distance between the data point and all other data points within the same cluster (intra-cluster distance).
• b: Distance between the data point and the nearest cluster that the data point doesn’t belong to (inter-cluster distance).

The silhouette score for a data point is then calculated as:

(b – a) / max(a, b)

Interpretation:

The silhouette score ranges from -1 to 1:

• 1: Ideally close data points within a cluster and far away from other clusters (good clustering).
• 0: Data points are on the border between clusters, indicating some overlap (average clustering).
• -1: Data points might be assigned to the wrong cluster (poor clustering).

Using Silhouette Score:

The silhouette score is particularly helpful in determining the optimal number of clusters (k) for K-means. You can calculate the silhouette score for different values of k and choose the k that results in the highest average silhouette score. This indicates a clustering where data points are well-separated within their clusters.

Here are some additional points to consider:

• Silhouette analysis can be visualized using a silhouette plot, which helps identify clusters with low silhouette score interpretation.
• Silhouette score is just one metric for evaluating K-means clustering. Other factors, such as domain knowledge and the purpose of clustering, should also be considered.
• Some libraries like scikit-learn in Python provide functions to calculate k-means silhouette score for K-means clustering.

Methods to Find the Best Value of K

This blog will discuss the most important parameter, how to select an optimal number of clusters (K). Two main methods exist to find the best value of K. We will discuss them individually.

Elbow Curve Method

Remember that partitioning methods, such as k-means clustering, aim to define clusters to minimise the total intra-cluster variation (or total within-cluster sum of squares, WSS). The total WSS measures the compactness of the clustering, and we want it to be as small as possible. The elbow method runs k-means clustering (kmeans number of clusters) on the dataset for a range of k (say 1 to 10) In the elbow method, we plot mean distance and look for the elbow point where the rate of decrease shifts. For each k, calculate the total within-cluster sum of squares (WSS). This elbow point can be used to determine K.

• We perform K-means clustering with all these different values of K. For each of the K values, we calculate the average distances to the centroid across all data points.
• Plot these points and find where the average distance from the centroid falls suddenly (“Elbow”).

At first, clusters will give a lot of information (about variance), but at some point, the marginal gain will drop, giving an angle in the graph. The number of clusters is chosen at this point, hence the “elbow criterion”. This “elbow” can’t always be unambiguously identified.

Inertia: Sum of squared distances of samples to their closest cluster centre.

We always lack clear clustered data, which means that the elbow may not be clear and sharp.

Let us see the Python code with the help of an example.

Python Code:

#You can adjust the size of the floating window in order to view the results properly

import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
import sklearn
from sklearn.cluster import KMeans
from sklearn.metrics import silhouette_score
X1 = [3, 1, 1, 2, 1, 6, 6, 6, 5, 6, 7, 8, 9, 8, 9, 9, 8]
X2 = [5, 4, 5, 6, 5, 8, 6, 7, 6, 7, 1, 2, 1, 2, 3, 2, 3]
plt.scatter(X1,X2)
plt.show()

The optimal number of clusters should be around 3. However, visualizing the data alone cannot always give the right answer.

Sum_of_squared_distances = []
K = range(1,10)
for num_clusters in K :
 kmeans = KMeans(n_clusters=num_clusters)
 kmeans.fit(data_frame)
 Sum_of_squared_distances.append(kmeans.inertia_)
plt.plot(K,Sum_of_squared_distances,’bx-’)
plt.xlabel(‘Values of K’) 
plt.ylabel(‘Sum of squared distances/Inertia’) 
plt.title(‘Elbow Method For Optimal k’)
plt.show()

The curve looks like an elbow. In the above plot, the elbow is at k=3 (i.e., the Sum of squared distances falls suddenly), indicating the optimal k for this dataset is 3.

Silhouette Analysis

The silhouette coefficient or v in k-means clustering measures the similarity of a data point within its cluster (cohesion) compared to other clusters (separation). You can easily calculate the silhouette score in Python using the metrics module of the scikit-learn/sklearn library.

• Select a range of values of k (say 1 to 10).
• Plot Silhouette analysis coefficient for each value of K.

The equation for calculating the silhouette coefficient for a particular data point:

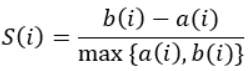
• S(i) is the silhouette coefficient of the data point i.
• a(i) is the average distance between i and all the other data points in the cluster to which i belongs.
• b(i) is the average distance from i to all clusters to which i does not belong.

We will then calculate the average_silhouette for every k.

Then plot the graph between average_silhouette and K.

Points to Remember While Calculating Silhouette Coefficient:

• The value of the silhouette analysis coefficient is between [-1, 1].
• A score of 1 denotes the best, meaning that the data point i is very compact within the cluster it belongs to and far away from the other clusters.
• The worst value is -1. Values near 0 denote overlapping clusters.

Let us see the Python code with the help of an example.

range_n_clusters = [2, 3, 4, 5, 6, 7, 8]
silhouette_avg = []
for num_clusters in range_n_clusters:
 
 # initialise kmeans
 kmeans = KMeans(n_clusters=num_clusters)
 kmeans.fit(data_frame)
 cluster_labels = kmeans.labels_
 
 # silhouette score
 silhouette_avg.append(silhouette_score(data_frame, cluster_labels))plt.plot(range_n_clusters,silhouette_avg,’bx-’)
plt.xlabel(‘Values of K’) 
plt.ylabel(‘Silhouette score’) 
plt.title(‘Silhouette analysis For Optimal k’)
plt.show()

The k means silhouette score is maximized at k = 3. So, we will take 3 clusters.

NOTE: The silhouette analysis Method is combined with the Elbow Method for a more confident decision.

What Is Hierarchical Clustering?

In k-means clustering, you have to predetermine the number of clusters you want to divide your data points into, i.e., the value of K, whereas in Hierarchical clustering, the data automatically forms a tree shape (dendrogram).

So, how do we decide which clustering to select? We choose either of them depending on our problem statement and business requirements.

Hierarchical clustering gives you a deep insight into each step of converging different clusters and creates a dendrogram. It helps you to figure out which cluster combination makes more sense. Mixture models are probabilistic models that identify the probability of having clusters in the overall population. K-means is a fast and simple clustering method that can sometimes not capture inherent heterogeneity. K-means is simple and efficient, and it is also used for image segmentation, providing good results for many more complex deep neural network algorithms.

Conclusion

The K-means clustering algorithm is an unsupervised algorithm used to find clusters in the dataset that have not been labelled. This method can help confirm business assumptions about the types of existing groups or identify unknown groups in complex datasets. In this tutorial, we learned how to find optimal cluster numbers. Also, you will learn about the Silhouette Score Kmeans, which tells what that means and how to learn it.

Hope you like the article. We have covered many important things i.e. silhouette score, silhouette analysis

Key Takeaways

• With clustering, data scientists can discover intrinsic grouping among unlabelled data.
•  K-means is mostly used in customer insight, marketing, medical, and social media.