Interview Prep
Career
GenAI
Prompt Engg
ChatGPT
LLM
Langchain
RAG
AI Agents
Machine Learning
Deep Learning
GenAI Tools
LLMOps
Python
NLP
SQL
AIML Projects

Reading list

Machine Learning Basics for a Newbie
6 Steps of Machine learning Lifecycle Introduction to Predictive Modeling
Introduction to Exploratory Data Analysis & Data Insights Descriptive Statistics Inferential Statistics How to Understand Population Distributions?
Reading Data Files into Python Different Variable Datatypes
Probability for Data Science Basic Concepts of Probability Axioms of Probability Conditional Probability
Central Tendencies for Continuous Variables Spread of Data KDE plots for Continuous Variable Overview of Distribution for Continuous variables Normal Distribution Skewed Distribution Skeweness and Kurtosis Distribution for Continuous Variable
Central Tendencies for Categorical Variables Understanding Discrete Distributions Performing EDA on Categorical Variables
Dealing with Missing Values Understanding Outliers Identifying Outliers in Data Outlier Detection in Python Outliers Detection Using IQR, Z-score, LOF and DBSCAN
Sample and Population Central Limit Theorem Confidence Interval and Margin of Error
Bivariate Analysis Introduction
Covariance Pearson Correlation Spearman's Correlation & Kendall's Tau Correlation versus Causation Tabular and Graphical methods for Bivariate Analysis Performing Bivariate Analysis on Continuous-Continuous Variables
Tabular and Graphical methods for Continuous-Categorical Variables Introduction to Hypothesis Testing P-value Two sample Z-test T-test T-test vs Z-test Performing Bivariate Analysis on Continuous-Catagorical variables
Chi-Squares Test Bivariate Analysis on Categorical Categorical Variables
Multivariate Analysis A Comprehensive Guide to Data Exploration The Data Science behind IPL
Supervised Learning vs Unsupervised Learning Reinforcement Learning Generative and Descriminative Models Parametric and Non Parametric model
Machine Learning Pipeline Preparing Dataset Build a Benchmark Model: Regression Build a Benchmark Model: Classification
Evaluation Metrics for Machine Learning Everyone should know Confusion Matrix Accuracy Precision and Recall AUC-ROC Log Loss R2 and Adjusted R2
Dealing with Missing Values Replacing Missing Values Imputing Missing Values in Data Working with Categorical Variables Working with Outliers Preprocessing Data for Model Building
Understanding Cost Function Understanding Gradient Descent Math Behind Gradient Descent Assumptions of Linear Regression Implement Linear Regression from Scratch Train Linear Regression in Python Implementing Linear Regression in R Diagnosing Residual Plots in Linear Regression Models Generalized Linear Models Introduction to Logistic Regression Odds Ratio Implementing Logistic Regression from Scratch Introduction to Scikit-learn in Python Train Logistic Regression in python Multiclass using Logistic Regression How to use Multinomial and Ordinal Logistic Regression in R ? Challenges with Linear Regression Introduction to Regularisation Implementing Regularisation Ridge Regression Lasso Regression
Introduction to K Nearest Neighbours Determining the Right Value of K in KNN Implement KNN from Scratch Implement KNN in Python
Bias Variance Tradeoff Introduction to Overfitting and Underfitting Visualizing Overfitting and Underfitting Selecting the Right Model What is Validation? Hold-Out Validation Understanding K Fold Cross Validation
Introduction to Feature Selection Feature Selection Algorithms Missing Value Ratio Low Variance Filter High Correlation Filter Backward Feature Elimination Forward Feature Selection Implement Feature Selection in Python Implement Feature Selection in R
Introduction to Decision Tree Purity in Decision Tree Terminologies Related to Decision Tree How to Select Best Split Point in Decision Tree? Chi-Squares Information Gain Reduction in Variance Optimizing Performance of Decision Tree Train Decision Tree using Scikit Learn Pruning of Decision Trees
Introduction to Feature Engineering Feature Transformation Feature Scaling Feature Engineering Frequency Encoding Automated Feature Engineering: Feature Tools
Introduction to Naive Bayes Conditional Probability and Bayes Theorem Introduction to Bayesian Adjustment Rating: The Incredible Concept Behind Online Ratings! Working of Naive Bayes Math behind Naive Bayes Types of Naive Bayes Implementation of Naive Bayes
Understanding how to solve Multiclass and Multilabled Classification Problem Evaluation Metrics: Multi Class Classification
Introduction to Ensemble Techniques Basic Ensemble Techniques Implementing Basic Ensemble Techniques Finding Optimal Weights of Ensemble Learner using Neural Network Why Ensemble Models Work well?
Introduction to Stacking Implementing Stacking Variants of Stacking Implementing Variants of Stacking Introduction to Blending Bootstrap Sampling Introduction to Random Sampling Hyper-parameters of Random Forest Implementing Random Forest Out-of-Bag (OOB) Score in the Random Forest IPL Team Win Prediction Project Using Machine Learning Introduction to Boosting Gradient Boosting Algorithm Math behind GBM Implementing GBM in python Regularized Greedy Forests Extreme Gradient Boosting Implementing XGBM in python Tuning Hyperparameters of XGBoost in Python Implement XGBM in R/H2O Adaptive Boosting Implementing Adaptive Boosing LightGBM Implementing LightGBM in Python Catboost Implementing Catboost in Python
Different Hyperparameter Tuning methods Implementing Different Hyperparameter Tuning methods GridsearchCV RandomizedsearchCV Bayesian Optimization for Hyperparameter Tuning Hyperopt
Understanding SVM Algorithm SVM Kernels In-depth Intuition and Practical Implementation SVM Kernel Tricks Kernels and Hyperparameters in SVM Implementing SVM from Scratch in Python and R
Introduction to Principal Component Analysis Steps to Perform Principal Compound Analysis Computation of Covariance Matrix Finding Eigenvectors and Eigenvalues Implementing PCA in python Visualizing PCA A Brief Introduction to Linear Discriminant Analysis Introduction to Factor Analysis
Introduction to Clustering Applications of Clustering Evaluation Metrics for Clustering Understanding K-Means Implementation of K-Means in Python Implementation of K-Means in R Choosing Right Value for K Profiling Market Segments using K-Means Clustering Hierarchical Clustering Implementation of Hierarchial Clustering DBSCAN Defining Similarity between clusters Build Better and Accurate Clusters with Gaussian Mixture Models
Understand Basics of Recommendation Engine with Case Study
8 Ways to Improve Accuracy of Machine Learning Models
Introduction to Dask Working with CuML
Introduction to Machine Learning Interpretability Framework and Interpretable Models model Agnostic Methods for Interpretability Implementing Interpretable Model Understanding SHAP Out-of-Core ML Introduction to Interpretable Machine Learning Models Model Agnostic Methods for Interpretability Game Theory & Shapley Values
Introduction to Machine Learning Interpretability Framework and Interpretable Models model Agnostic Methods for Interpretability Implementing Interpretable Model Understanding SHAP Out-of-Core ML Introduction to Interpretable Machine Learning Models Model Agnostic Methods for Interpretability Game Theory & Shapley Values
Introduction to AutoML Implementation of MLBox Introduction to PyCaret TPOT Auto-Sklearn EvalML
Pickle and Joblib Introduction to Model Deployment
Deploying Machine Learning Model using Streamlit Deploying ML Models in Docker Deploy Using Streamlit Deploy on Heroku Deploy Using Netlify Introduction to Amazon Sagemaker Setting up Amazon SageMaker Using SageMaker Endpoint to Generate Inference Deploy on Microsoft Azure Cloud Introduction to Flask for Model Deploying ML model using Flask
Model Deployment in Android Model Deployment in Iphone

Machine Learning Model Evaluation

Shiv
Shiv Last Updated : 06 May, 2021
6 min read

What is Machine Learning?

Machine Learning is a popular topic in Information Technology in the present day. Machine Learning allows our computer to gain insight from data and experience just as a human being would. In Machine Learning, programmers teach the computer how to use its past experiences with different entities to perform better in future scenarios.

Machine Learning involves constructing mathematical models to help us understand the data at hand. Once these models have been fitted to previously seen data, they can be used to predict newly observed data.

In Machine Learning, models are only as useful as their quality of predictions; hence, fundamentally our goal is not to create models but to create high-quality models with promising predictive power. We shall now examine strategies for evaluating the quality of models that are generated by our Machine Learning Algorithms.

Why you should study AI and Machine Learning and how I did it | Nokia

Source: Nokia Corporation.

Evaluating Binary Classifier Predictions.

When it comes to evaluating a Binary Classifier, Accuracy is a well-known performance metric that is used to tell a strong classification model from one that is weak. Accuracy is, simply put, the total proportion of observations that have been correctly predicted. There are four (4) main components that comprise the mathematical formula for calculating Accuracy, viz. TP, TN, FP, FN, and these components grant us the ability to explore other ML Model Evaluation Metrics. The formula for calculating accuracy is as follows:

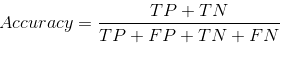
Equation_Accuracy

Source: My PC

Where:

  • TP represents the number of True Positives. This refers to the total number of observations that belong to the positive class and have been predicted correctly.
  • TN represents the number of True Negatives. This is the total number of observations that belong to the negative class and have been predicted correctly.
  • FP is the number of False Positives. It is also known as a Type 1 Error. This is the total number of observations that have been predicted to belong to the positive class, but instead, actually, belong to the negative class.
  • FN is the number of False Negatives. It may be
    referred to as a Type 2 Error. This is the total number of observations that
    have been predicted to be a part of the negative class but instead belong to
    the positive class.

The main reason for individuals to utilize the Accuracy Evaluation Metric is for ease of use. This Evaluation Metric has a simple approach and explanation. It is, as discussed before, simply the total proportion (total number) of observations that have been predicted correctly. Accuracy, however, is an Evaluation Metric that does not perform well when the presence of imbalanced classes-when in the presence of imbalanced classes, Accuracy suffers from a paradox; i.e., where the Accuracy value is high but the model lacks predictive power and most, if not all, predictions are going to be incorrect.

For the above reason, when we are unable to use the Accuracy Evaluation Metric, we are compelled to turn to other evaluation metrics in the scikit-learn arsenal. These include, but are not limited to, the following Evaluation Metrics:

Precision

This refers to the proportion (total number) of all observations that have been predicted to belong to the positive class and are actually positive. The formula for Precision Evaluation Metric is as follows:

Confusion matrix Precision Model Evaluation Machine Learning

Source: My PC

Recall

This is the proportion of observation predicted to belong to the positive class, that truly belongs to the positive class. It indirectly tells us the model’s ability to randomly identify an observation that belongs to the positive class. The formula for Recall is as follows:

Confusion matrix Recall Model Evaluation Machine Learning

Source: My PC

F1 Score.

This is an averaging Evaluation Metric that is used to generate a ratio. The F1 Score is also known as the Harmonic Mean of the precision and recall Evaluation Metrics. This Evaluation Metric is a measure of overall correctness that our model has achieved in a positive prediction environment-
i.e., Of all observations that our model has labeled as positive, how many of these observations are actually positive. The formula for the F1 Score
Evaluation Metric is as follows:

f1 score Model Evaluation Machine Learning

Source: My PC

Evaluating Multiclass Classifier Predictions.

As we have learned from earlier information in the article, in Machine Learning, all input data is not balanced, hence the issue of Imbalanced Classes. With the Accuracy Evaluation Metric removed from our options, we specifically turn to Precision, Recall, and F1 Scores. We use parameter
options in Python, which are used for aggregating the evaluation values by averaging them. The three main options that we have available to us are:

  1. _macro – Here we specify to the compiler to calculate the mean of metric scores for each class in the dataset, weighting each class equally.
  2. _weighted – We calculate the mean of metric scores for each class, and we weigh each class directly proportional to its size in the dataset.
  3. _micro – Here we calculate the mean of metric
    scores for each OBSERVATION in the dataset.

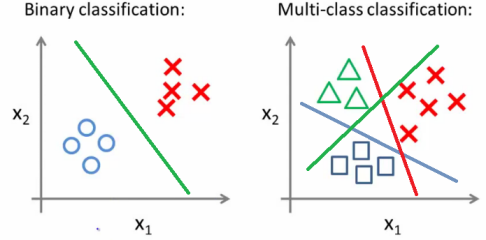
Tips and Tricks for Multi-Class Classification | by Mohammed Terry-Jack | Medium

Source: Medium.

Visualizing a Classifier’s Performance.

Currently, the most popular way to visualize a classifier’s performance is through a Confusion Matrix. A Confusion Matrix may be referred to as an Error Matrix. A Confusion Matrix has a high level of interpretability. It comprises a simple tabular format, which is often generated and visualized as a Heatmap. Each Column of the Confusion Matrix represents the predicted classes, while every row shows the true (or actual) classes.

There are three important facts to be aware of about a Confusion Matrix:

  1. A Perfect Confusion Matrix will have values along the main diagonal (from left to right), and there will zeroes (0) everywhere else in the confusion matrix.
  2. A Confusion Matrix does not only show us where the Machine Learning Model faltered but also how it reached those conclusions.
  3. A Confusion Matrix will function with any number
    of classes, i.e., Having a dataset containing 50 classes, will not affect model
    performance nor the Confusion Matrix- it just means your Visualized Matrix will
    be very large in size.

Confusion Matrix for LWL Classifiers -IRIS Dataset | Download Table Model Evaluation Machine Learning

Source: ResearchGate.

Evaluating a Regression Model’s Performance.

For a Regressor, you will find that one of the most used and well-known Evaluation Metrics is MSE. MSE stands for Mean Squared Error. Put into a mathematical representation, MSE is calculated as follows:

Model Evaluation Machine Learning MSE

Source: My PC.

Where:

  • n represents the number of observations in the dataset.
  • yi is the true value of the target value we are trying to predict for observation I.
  • ŷi is the model’s predicted value for yi.

MSE is a calculation that involves finding the squared sum of all the distances between predicted and true values. The higher the output value for MSE, the greater the sum of squared error present in the model, and hence, the worse the quality of model predictions. There are advantages of squaring the error margins, as seen in the model:

  • Firstly, squaring the error constrains all error values to be positive.
  • Secondly, this means the model will penalize few
    large error values, more than it will penalize many small error values.

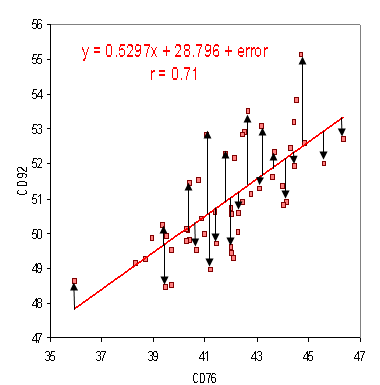
RMSE: Root Mean Square Error - Statistics How To Model Evaluation Machine Learning

Source: Statistics How To.

This concludes my article on Machine Learning Model Evaluation.

Thank you for your time.

The media shown in this article are not owned by Analytics Vidhya and is used at the Author’s discretion. 

blogathonModel evaluation
Shiv
Shiv

Free Courses

Generative AI 4.7

Generative AI - A Way of Life

Explore Generative AI for beginners: create text and images, use top AI tools, learn practical skills, and ethics.
Large Language Models 4.5

Getting Started with Large Language Models

Master Large Language Models (LLMs) with this course, offering clear guidance in NLP and model training made simple.
Prompt Engineering 4.6

Building LLM Applications using Prompt Engineering

This free course guides you on building LLM apps, mastering prompt engineering, and developing chatbots with enterprise data.
LlamaIndex 4.8

Improving Real World RAG Systems: Key Challenges & Practical Solutions

Explore practical solutions, advanced retrieval strategies, and agentic RAG systems to improve context, relevance, and accuracy in AI-driven applications.
RAG systems using LlamaIndex 4.7

Microsoft Excel: Formulas & Functions

Master MS Excel for data analysis with key formulas, functions, and LookUp tools in this comprehensive course.

Recommended Articles

Responses From Readers

Clear

Write for us

Write, captivate, and earn accolades and rewards for your work
  • Reach a Global Audience
  • Get Expert Feedback
  • Build Your Brand & Audience
  • Cash In on Your Knowledge
  • Join a Thriving Community
  • Level Up Your Data Science Game
imag
Congratulations, You Did It!
Well Done on Completing Your Learning Journey. Stay curious and keep exploring!
12 Important Model Evaluation Metrics for Machine Learning Everyone Should Know (Updated 2024)
12 Important Model Evaluation Metrics for Machine Learning Everyone Should Know (Updated 2024)
Evaluation Metrics With Python Codes
Evaluation Metrics With Python Codes

We use cookies essential for this site to function well. Please click to help us improve its usefulness with additional cookies. Learn about our use of cookies in our Privacy Policy & Cookies Policy.

Show details