Interview Prep
Career
GenAI
Prompt Engg
ChatGPT
LLM
Langchain
RAG
AI Agents
Machine Learning
Deep Learning
GenAI Tools
LLMOps
Python
NLP
SQL
AIML Projects

Reading list

Machine Learning Basics for a Newbie
6 Steps of Machine learning Lifecycle Introduction to Predictive Modeling
Introduction to Exploratory Data Analysis & Data Insights Descriptive Statistics Inferential Statistics How to Understand Population Distributions?
Reading Data Files into Python Different Variable Datatypes
Probability for Data Science Basic Concepts of Probability Axioms of Probability Conditional Probability
Central Tendencies for Continuous Variables Spread of Data KDE plots for Continuous Variable Overview of Distribution for Continuous variables Normal Distribution Skewed Distribution Skeweness and Kurtosis Distribution for Continuous Variable
Central Tendencies for Categorical Variables Understanding Discrete Distributions Performing EDA on Categorical Variables
Dealing with Missing Values Understanding Outliers Identifying Outliers in Data Outlier Detection in Python Outliers Detection Using IQR, Z-score, LOF and DBSCAN
Sample and Population Central Limit Theorem Confidence Interval and Margin of Error
Bivariate Analysis Introduction
Covariance Pearson Correlation Spearman's Correlation & Kendall's Tau Correlation versus Causation Tabular and Graphical methods for Bivariate Analysis Performing Bivariate Analysis on Continuous-Continuous Variables
Tabular and Graphical methods for Continuous-Categorical Variables Introduction to Hypothesis Testing P-value Two sample Z-test T-test T-test vs Z-test Performing Bivariate Analysis on Continuous-Catagorical variables
Chi-Squares Test Bivariate Analysis on Categorical Categorical Variables
Multivariate Analysis A Comprehensive Guide to Data Exploration The Data Science behind IPL
Supervised Learning vs Unsupervised Learning Reinforcement Learning Generative and Descriminative Models Parametric and Non Parametric model
Machine Learning Pipeline Preparing Dataset Build a Benchmark Model: Regression Build a Benchmark Model: Classification
Evaluation Metrics for Machine Learning Everyone should know Confusion Matrix Accuracy Precision and Recall AUC-ROC Log Loss R2 and Adjusted R2
Dealing with Missing Values Replacing Missing Values Imputing Missing Values in Data Working with Categorical Variables Working with Outliers Preprocessing Data for Model Building
Understanding Cost Function Understanding Gradient Descent Math Behind Gradient Descent Assumptions of Linear Regression Implement Linear Regression from Scratch Train Linear Regression in Python Implementing Linear Regression in R Diagnosing Residual Plots in Linear Regression Models Generalized Linear Models Introduction to Logistic Regression Odds Ratio Implementing Logistic Regression from Scratch Introduction to Scikit-learn in Python Train Logistic Regression in python Multiclass using Logistic Regression How to use Multinomial and Ordinal Logistic Regression in R ? Challenges with Linear Regression Introduction to Regularisation Implementing Regularisation Ridge Regression Lasso Regression
Introduction to K Nearest Neighbours Determining the Right Value of K in KNN Implement KNN from Scratch Implement KNN in Python
Bias Variance Tradeoff Introduction to Overfitting and Underfitting Visualizing Overfitting and Underfitting Selecting the Right Model What is Validation? Hold-Out Validation Understanding K Fold Cross Validation
Introduction to Feature Selection Feature Selection Algorithms Missing Value Ratio Low Variance Filter High Correlation Filter Backward Feature Elimination Forward Feature Selection Implement Feature Selection in Python Implement Feature Selection in R
Introduction to Decision Tree Purity in Decision Tree Terminologies Related to Decision Tree How to Select Best Split Point in Decision Tree? Chi-Squares Information Gain Reduction in Variance Optimizing Performance of Decision Tree Train Decision Tree using Scikit Learn Pruning of Decision Trees
Introduction to Feature Engineering Feature Transformation Feature Scaling Feature Engineering Frequency Encoding Automated Feature Engineering: Feature Tools
Introduction to Naive Bayes Conditional Probability and Bayes Theorem Introduction to Bayesian Adjustment Rating: The Incredible Concept Behind Online Ratings! Working of Naive Bayes Math behind Naive Bayes Types of Naive Bayes Implementation of Naive Bayes
Understanding how to solve Multiclass and Multilabled Classification Problem Evaluation Metrics: Multi Class Classification
Introduction to Ensemble Techniques Basic Ensemble Techniques Implementing Basic Ensemble Techniques Finding Optimal Weights of Ensemble Learner using Neural Network Why Ensemble Models Work well?
Introduction to Stacking Implementing Stacking Variants of Stacking Implementing Variants of Stacking Introduction to Blending Bootstrap Sampling Introduction to Random Sampling Hyper-parameters of Random Forest Implementing Random Forest Out-of-Bag (OOB) Score in the Random Forest IPL Team Win Prediction Project Using Machine Learning Introduction to Boosting Gradient Boosting Algorithm Math behind GBM Implementing GBM in python Regularized Greedy Forests Extreme Gradient Boosting Implementing XGBM in python Tuning Hyperparameters of XGBoost in Python Implement XGBM in R/H2O Adaptive Boosting Implementing Adaptive Boosing LightGBM Implementing LightGBM in Python Catboost Implementing Catboost in Python
Different Hyperparameter Tuning methods Implementing Different Hyperparameter Tuning methods GridsearchCV RandomizedsearchCV Bayesian Optimization for Hyperparameter Tuning Hyperopt
Understanding SVM Algorithm SVM Kernels In-depth Intuition and Practical Implementation SVM Kernel Tricks Kernels and Hyperparameters in SVM Implementing SVM from Scratch in Python and R
Introduction to Principal Component Analysis Steps to Perform Principal Compound Analysis Computation of Covariance Matrix Finding Eigenvectors and Eigenvalues Implementing PCA in python Visualizing PCA A Brief Introduction to Linear Discriminant Analysis Introduction to Factor Analysis
Introduction to Clustering Applications of Clustering Evaluation Metrics for Clustering Understanding K-Means Implementation of K-Means in Python Implementation of K-Means in R Choosing Right Value for K Profiling Market Segments using K-Means Clustering Hierarchical Clustering Implementation of Hierarchial Clustering DBSCAN Defining Similarity between clusters Build Better and Accurate Clusters with Gaussian Mixture Models
Understand Basics of Recommendation Engine with Case Study
8 Ways to Improve Accuracy of Machine Learning Models
Introduction to Dask Working with CuML
Introduction to Machine Learning Interpretability Framework and Interpretable Models model Agnostic Methods for Interpretability Implementing Interpretable Model Understanding SHAP Out-of-Core ML Introduction to Interpretable Machine Learning Models Model Agnostic Methods for Interpretability Game Theory & Shapley Values
Introduction to Machine Learning Interpretability Framework and Interpretable Models model Agnostic Methods for Interpretability Implementing Interpretable Model Understanding SHAP Out-of-Core ML Introduction to Interpretable Machine Learning Models Model Agnostic Methods for Interpretability Game Theory & Shapley Values
Introduction to AutoML Implementation of MLBox Introduction to PyCaret TPOT Auto-Sklearn EvalML
Pickle and Joblib Introduction to Model Deployment
Deploying Machine Learning Model using Streamlit Deploying ML Models in Docker Deploy Using Streamlit Deploy on Heroku Deploy Using Netlify Introduction to Amazon Sagemaker Setting up Amazon SageMaker Using SageMaker Endpoint to Generate Inference Deploy on Microsoft Azure Cloud Introduction to Flask for Model Deploying ML model using Flask
Model Deployment in Android Model Deployment in Iphone

Machine Learning with Python: Logistic Regression

Shiv
Shiv Last Updated : 15 Dec, 2023
5 min read

This article was published as a part of the Data Science Blogathon.

What Is Logistic Regression?

This article assumes that you possess basic knowledge and understanding of Machine Learning Concepts, such as Target Vector, Features Matrix, and related terms.

Logistic Regression, probably one of the most interesting Supervised Machine Learning Algorithms in Machine Learning, stands out. Despite having “Regression” in its name, Logistic Regression is a popularly used Supervised Classification Algorithm in machine learning Python. Logistic Regression, along with its related cousins, such as Multinomial Logistic Regression, grants us the ability to predict whether an observation belongs to a certain class using an approach that is straightforward, easy-to-understand, and follows the principles of logistic regression in machine learning Python.

Simplifying Logistic Regression - DZone AI, logistic regression in machine learning python

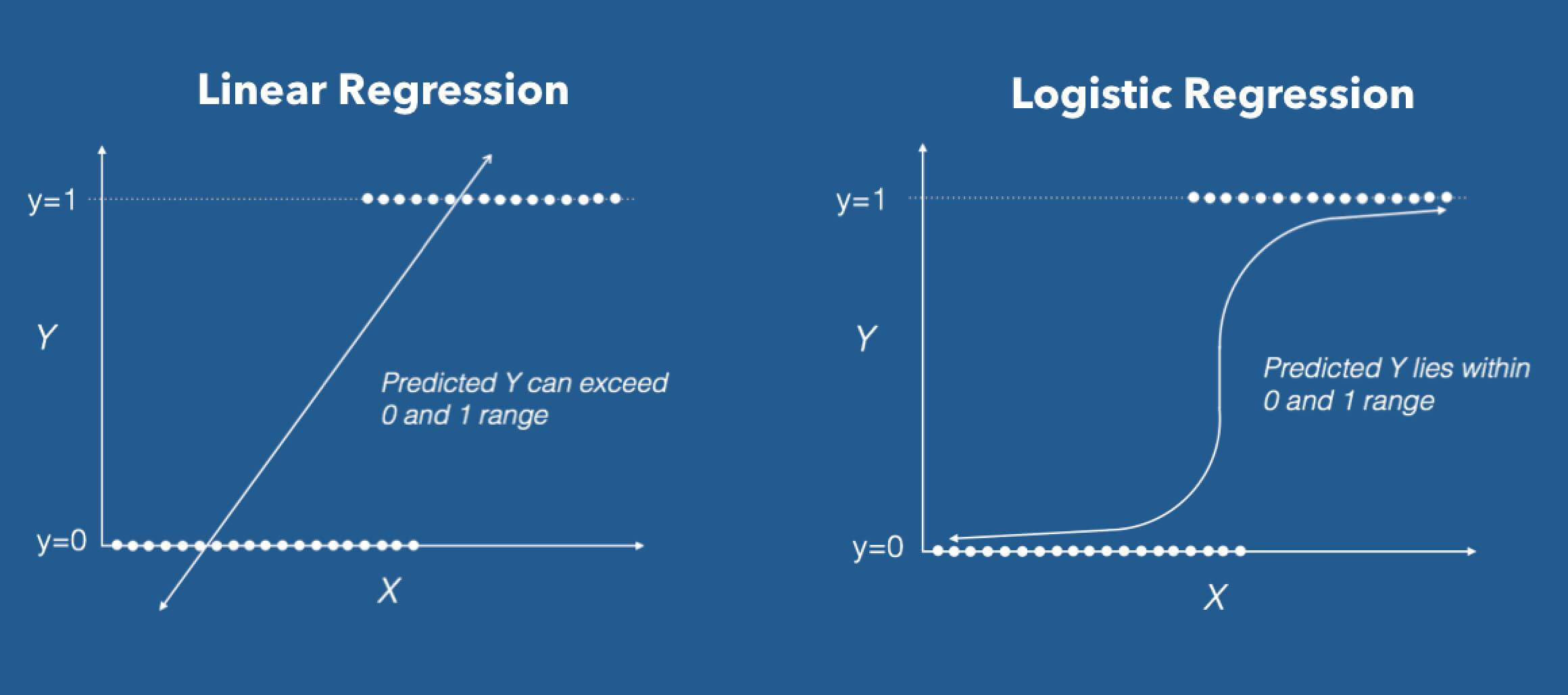
Source: DZone

Logistic Regression in its base form (by default) is a Binary Classifier. This means that the target vector may only take the form of one of two values. In the Logistic Regression Algorithm formula, we have a Linear Model, e.g., β0 + β1x, that is integrated into a Logistic Function (also known as a Sigmoid Function). The Binary Classifier formula that we have at the end is as follows:

Where:

  • P(yi = 1 | X) is the probability of the ith observations target value, yi belonging to class 1.
  • Β0 and β1 are the parameters that are to be learned.
  • e represents Euler’s Number.

Main Aim of Logistic Regression Formula.

The Logistic Regression formula aims to limit or constrain the Linear and/or Sigmoid output between a value of 0 and 1. The main reason is for interpretability purposes, i.e., we can read the value as a simple Probability; Meaning that if the value is greater than 0.5 class one would be predicted, otherwise, class 0 is predicted.

Main Aim of Logistic Regression formula

Source: GraphPad

Python Implementation.

We shall now look at the implementation of the Python Programming Language. For this exercise, we will be using the Ionosphere dataset which is available for download from the UCI Machine Learning Repository.

# We begin by importing the necessary packages
# to be used for the Machine Learning problem

import pandas as pd
import numpy as np
from sklearn.linear_model import LogisticRegression
from sklearn.preprocessing import StandardScaler

# We read the data into our system using Pandas'
# 'read_csv' method. This transforms the .csv file
# into a Pandas DataFrame object.

dataframe = pd.read_csv('ionosphere.data', header=None)

# We configure the display settings of the
# Pandas DataFrame.

pd.set_option('display.max_rows', 10000000000)
pd.set_option('display.max_columns', 10000000000)
pd.set_option('display.width', 95)

# We view the shape of the dataframe. Specifically
# the number of rows and columns present.
print('This DataFrame Has %d Rows and %d Columns'%(dataframe.shape))

Output to the above code would be as follows (the shape of the dataframe):

code 4
# We print the first five rows of our dataframe.
print(dataframe.head())

Output to the above code will be seen as follows (below output is truncated):

truncate
# We isolate the features matrix from the DataFrame.
features_matrix = dataframe.iloc[:, 0:34]

# We isolate the target vector from the DataFrame.
target_vector = dataframe.iloc[:, -1]

# We check the shape of the features matrix, and target vector.
print('The Features Matrix Has %d Rows And %d Column(s)'%(features_matrix.shape))
print('The Target Matrix Has %d Rows And %d Column(s)'%(np.array(target_vector).reshape(-1, 1).shape))

Output for the shape of our Features Matrix and Target Vector would be as below:

Features Matrix and Target Vector logistic regression
# We use scikit-learn's StandardScaler in order to
# preprocess the features matrix data. This will
# ensure that all values being inputted are on the same
# scale for the algorithm.

features_matrix_standardized = StandardScaler().fit_transform(features_matrix)
12 model predicted logistic regression
# We create an instance of the LogisticRegression Algorithm
# We utilize the default values for the parameters and
# hyperparameters.

algorithm = LogisticRegression(penalty='l2', dual=False, tol=1e-4,
C=1.0, fit_intercept=True,
intercept_scaling=1, class_weight=None,
random_state=None, solver='lbfgs',
max_iter=100, multi_class='auto',
verbose=0, warm_start=False, n_jobs=None,
l1_ratio=None)

# We utilize the 'fit' method in order to conduct the
# training process on our features matrix and target vector.

Logistic_Regression_Model = algorithm.fit(features_matrix_standardized, target_vector)
# We create an observation with values, in order
# to test the predictive power of our model.

observation = [[1, 0, 0.99539, -0.05889, 0.8524299999999999, 0.02306,
0.8339799999999999, -0.37708, 1.0, 0.0376,
0.8524299999999999, -0.17755, 0.59755, -0.44945, 0.60536,
-0.38223, 0.8435600000000001, -0.38542, 0.58212, -0.32192,
0.56971, -0.29674, 0.36946, -0.47357, 0.56811, -0.51171,
0.41078000000000003, -0.46168000000000003, 0.21266, -0.3409,
0.42267, -0.54487, 0.18641, -0.453]]
 
# We store the predicted class value in a variable
# called 'predictions'.

predictions = Logistic_Regression_Model.predict(observation)
# We print the model's predicted class for the observation.
print('The Model Predicted The Observation To Belong To Class %s'%(predictions))

Output to the above block of code should be as follows:

14 logistic regression
# We view the specific classes the model was trained to predict.

print('The Algorithm Was Trained To Predict One Of The Two Classes: %s'%(algorithm.classes_))

Output to the above code block will be seen as follows:

print("""The Model Says The Probability Of The Observation We Passed Belonging To Class ['b'] Is %s"""%(algorithm.predict_proba(observation)[0][0]))
print()
print("""The Model Says The Probability Of The Observation We Passed Belonging To Class ['g'] Is %s"""%(algorithm.predict_proba(observation)[0][1]))

The expected output would be as follows:

Logistic Regression model probability

Conclusion.

This concludes my article. We now understand the Logic behind this Supervised Machine Learning Algorithm and know how to implement it in a Binary Classification Problem.

Thank you for your time.

The media shown in this article are not owned by Analytics Vidhya and is used at the Author’s discretion. 

Frequently Asked Questions

Q1. What kind of problems is Logistic Regression best suited for?

 Logistic Regression is effective for problems like spam detection, medical diagnosis, and credit scoring, where binary outcomes need to be predicted.

Q2.How can I implement Logistic Regression in Python for my dataset?

 You can use libraries like scikit-learn to implement Logistic Regression easily. Code examples and tutorials are widely available online.

Q3.How does regularization impact Logistic Regression in Python?

 Regularization in Logistic Regression helps prevent overfitting by penalizing large coefficients. It’s valuable when dealing with complex datasets.

Shiv
Shiv

Free Courses

Generative AI 4.7

Generative AI - A Way of Life

Explore Generative AI for beginners: create text and images, use top AI tools, learn practical skills, and ethics.
Large Language Models 4.5

Getting Started with Large Language Models

Master Large Language Models (LLMs) with this course, offering clear guidance in NLP and model training made simple.
Prompt Engineering 4.6

Building LLM Applications using Prompt Engineering

This free course guides you on building LLM apps, mastering prompt engineering, and developing chatbots with enterprise data.
LlamaIndex 4.8

Improving Real World RAG Systems: Key Challenges & Practical Solutions

Explore practical solutions, advanced retrieval strategies, and agentic RAG systems to improve context, relevance, and accuracy in AI-driven applications.
RAG systems using LlamaIndex 4.7

Microsoft Excel: Formulas & Functions

Master MS Excel for data analysis with key formulas, functions, and LookUp tools in this comprehensive course.

Recommended Articles

Responses From Readers

Clear

Anshul
Anshul

Hello, Hope you are doing well. I was having some trouble with logistic regression and luckily I found your article. It is very well explained and really liked it. All the information was collectively present on one page. I still have some doubts and I was wondering if you could help me out. 1) Is there any derivation for the log loss function (from where did this function came)? 2) How does gradient descent work in logistic regression? Like in linear regression our y was (y = b0 + b1x) and what we did there was randomly select a value for b1 and then kept updating it until we get a minimum MSE or the global minima. Here, in Logistic regression, our (y = sigmoid function), just wanted to know how gradient descent will work here? In linear regression we used a random value for b1, what will be that random value in logistic regression? 3) After reading tons of articles I also got to know that logistic regression uses MLE(Maximum likelihood estimation). I couldn't figure out where exactly we use MLE in this algorithm I have read almost each and every article on google regarding these 3 topics but I couldn't get the perfect solution for this. It would be really helpful If you take out some time to help me out. Thanks Anshul Saini

123

Write for us

Write, captivate, and earn accolades and rewards for your work
  • Reach a Global Audience
  • Get Expert Feedback
  • Build Your Brand & Audience
  • Cash In on Your Knowledge
  • Join a Thriving Community
  • Level Up Your Data Science Game
imag

We use cookies essential for this site to function well. Please click to help us improve its usefulness with additional cookies. Learn about our use of cookies in our Privacy Policy & Cookies Policy.

Show details