Machine Learning with Python: Logistic Regression
This article was published as a part of the Data Science Blogathon.
What Is Logistic Regression?
This article assumes that you possess basic knowledge and understanding of Machine Learning Concepts, such as Target Vector, Features Matrix, and related terms.
Logistic Regression, probably one of the most interesting Supervised Machine Learning Algorithms in Machine Learning, stands out. Despite having “Regression” in its name, Logistic Regression is a popularly used Supervised Classification Algorithm in machine learning Python. Logistic Regression, along with its related cousins, such as Multinomial Logistic Regression, grants us the ability to predict whether an observation belongs to a certain class using an approach that is straightforward, easy-to-understand, and follows the principles of logistic regression in machine learning Python.
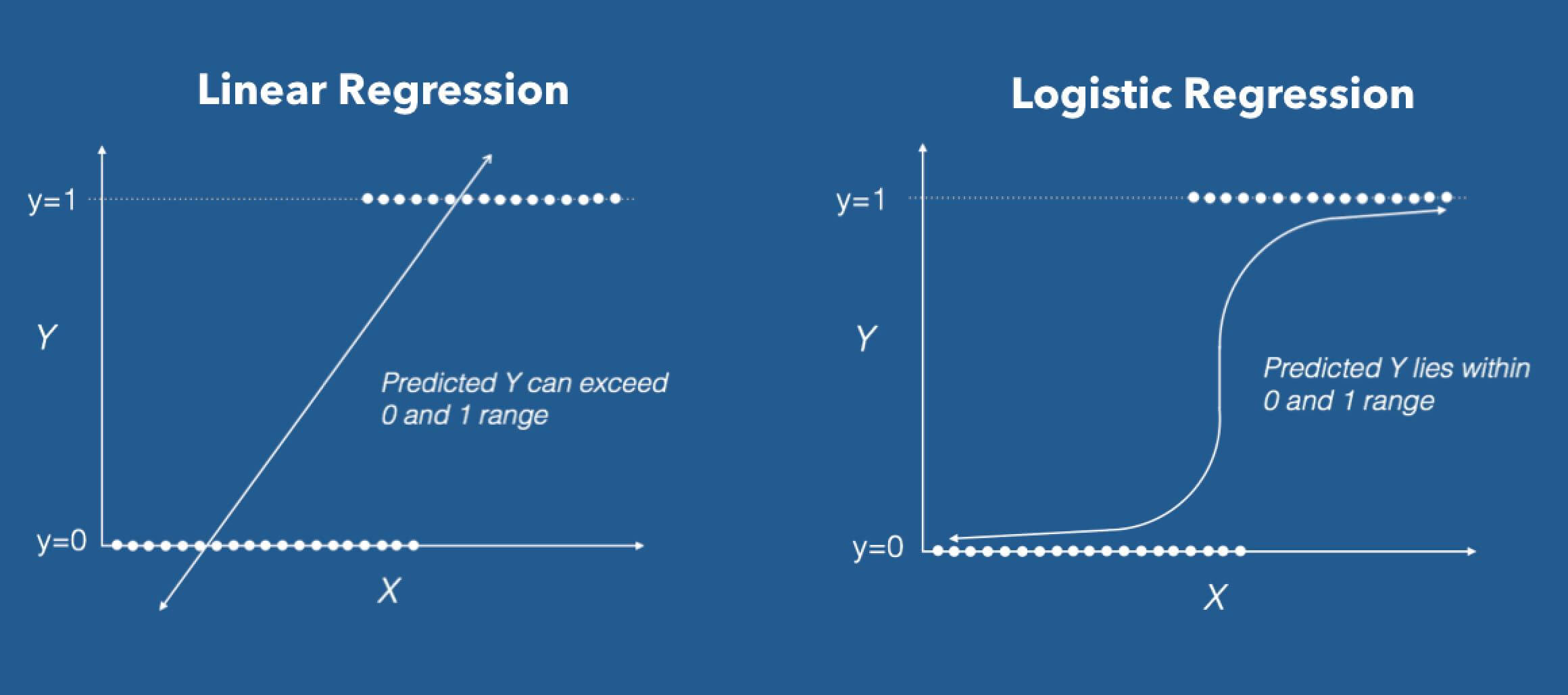
Source: DZone
Logistic Regression in its base form (by default) is a Binary Classifier. This means that the target vector may only take the form of one of two values. In the Logistic Regression Algorithm formula, we have a Linear Model, e.g., β0 + β1x, that is integrated into a Logistic Function (also known as a Sigmoid Function). The Binary Classifier formula that we have at the end is as follows:
Where:
- P(yi = 1 | X) is the probability of the ith observations target value, yi belonging to class 1.
- Β0 and β1 are the parameters that are to be learned.
- e represents Euler’s Number.
Main Aim of Logistic Regression Formula.
The Logistic Regression formula aims to limit or constrain the Linear and/or Sigmoid output between a value of 0 and 1. The main reason is for interpretability purposes, i.e., we can read the value as a simple Probability; Meaning that if the value is greater than 0.5 class one would be predicted, otherwise, class 0 is predicted.
Source: GraphPad
Python Implementation.
We shall now look at the implementation of the Python Programming Language. For this exercise, we will be using the Ionosphere dataset which is available for download from the UCI Machine Learning Repository.
# We begin by importing the necessary packages
# to be used for the Machine Learning problem
import pandas as pd
import numpy as np
from sklearn.linear_model import LogisticRegression
from sklearn.preprocessing import StandardScaler
# We read the data into our system using Pandas'
# 'read_csv' method. This transforms the .csv file
# into a Pandas DataFrame object.
dataframe = pd.read_csv('ionosphere.data', header=None)
# We configure the display settings of the
# Pandas DataFrame.
pd.set_option('display.max_rows', 10000000000)
pd.set_option('display.max_columns', 10000000000)
pd.set_option('display.width', 95)
# We view the shape of the dataframe. Specifically
# the number of rows and columns present.
print('This DataFrame Has %d Rows and %d Columns'%(dataframe.shape))Output to the above code would be as follows (the shape of the dataframe):
# We print the first five rows of our dataframe.
print(dataframe.head())Output to the above code will be seen as follows (below output is truncated):
# We isolate the features matrix from the DataFrame.
features_matrix = dataframe.iloc[:, 0:34]
# We isolate the target vector from the DataFrame.
target_vector = dataframe.iloc[:, -1]
# We check the shape of the features matrix, and target vector.
print('The Features Matrix Has %d Rows And %d Column(s)'%(features_matrix.shape))
print('The Target Matrix Has %d Rows And %d Column(s)'%(np.array(target_vector).reshape(-1, 1).shape))Output for the shape of our Features Matrix and Target Vector would be as below:
# We use scikit-learn's StandardScaler in order to
# preprocess the features matrix data. This will
# ensure that all values being inputted are on the same
# scale for the algorithm.
features_matrix_standardized = StandardScaler().fit_transform(features_matrix)# We create an instance of the LogisticRegression Algorithm
# We utilize the default values for the parameters and
# hyperparameters.
algorithm = LogisticRegression(penalty='l2', dual=False, tol=1e-4,
C=1.0, fit_intercept=True,
intercept_scaling=1, class_weight=None,
random_state=None, solver='lbfgs',
max_iter=100, multi_class='auto',
verbose=0, warm_start=False, n_jobs=None,
l1_ratio=None)
# We utilize the 'fit' method in order to conduct the
# training process on our features matrix and target vector.
Logistic_Regression_Model = algorithm.fit(features_matrix_standardized, target_vector)# We create an observation with values, in order # to test the predictive power of our model. observation = [[1, 0, 0.99539, -0.05889, 0.8524299999999999, 0.02306, 0.8339799999999999, -0.37708, 1.0, 0.0376, 0.8524299999999999, -0.17755, 0.59755, -0.44945, 0.60536, -0.38223, 0.8435600000000001, -0.38542, 0.58212, -0.32192, 0.56971, -0.29674, 0.36946, -0.47357, 0.56811, -0.51171, 0.41078000000000003, -0.46168000000000003, 0.21266, -0.3409, 0.42267, -0.54487, 0.18641, -0.453]]
# We store the predicted class value in a variable
# called 'predictions'.
predictions = Logistic_Regression_Model.predict(observation)# We print the model's predicted class for the observation.
print('The Model Predicted The Observation To Belong To Class %s'%(predictions))Output to the above block of code should be as follows:
# We view the specific classes the model was trained to predict.
print('The Algorithm Was Trained To Predict One Of The Two Classes: %s'%(algorithm.classes_))Output to the above code block will be seen as follows:
print("""The Model Says The Probability Of The Observation We Passed Belonging To Class ['b'] Is %s"""%(algorithm.predict_proba(observation)[0][0]))
print()
print("""The Model Says The Probability Of The Observation We Passed Belonging To Class ['g'] Is %s"""%(algorithm.predict_proba(observation)[0][1]))The expected output would be as follows:
Conclusion.
This concludes my article. We now understand the Logic behind this Supervised Machine Learning Algorithm and know how to implement it in a Binary Classification Problem.
Thank you for your time.
The media shown in this article are not owned by Analytics Vidhya and is used at the Author’s discretion.
Frequently Asked Questions
Logistic Regression is effective for problems like spam detection, medical diagnosis, and credit scoring, where binary outcomes need to be predicted.
You can use libraries like scikit-learn to implement Logistic Regression easily. Code examples and tutorials are widely available online.
Regularization in Logistic Regression helps prevent overfitting by penalizing large coefficients. It’s valuable when dealing with complex datasets.











Hello, Hope you are doing well. I was having some trouble with logistic regression and luckily I found your article. It is very well explained and really liked it. All the information was collectively present on one page. I still have some doubts and I was wondering if you could help me out. 1) Is there any derivation for the log loss function (from where did this function came)? 2) How does gradient descent work in logistic regression? Like in linear regression our y was (y = b0 + b1x) and what we did there was randomly select a value for b1 and then kept updating it until we get a minimum MSE or the global minima. Here, in Logistic regression, our (y = sigmoid function), just wanted to know how gradient descent will work here? In linear regression we used a random value for b1, what will be that random value in logistic regression? 3) After reading tons of articles I also got to know that logistic regression uses MLE(Maximum likelihood estimation). I couldn't figure out where exactly we use MLE in this algorithm I have read almost each and every article on google regarding these 3 topics but I couldn't get the perfect solution for this. It would be really helpful If you take out some time to help me out. Thanks Anshul Saini