Interview Prep
Career
GenAI
Prompt Engg
ChatGPT
LLM
Langchain
RAG
AI Agents
Machine Learning
Deep Learning
GenAI Tools
LLMOps
Python
NLP
SQL
AIML Projects

Reading list

Machine Learning Basics for a Newbie
6 Steps of Machine learning Lifecycle Introduction to Predictive Modeling
Introduction to Exploratory Data Analysis & Data Insights Descriptive Statistics Inferential Statistics How to Understand Population Distributions?
Reading Data Files into Python Different Variable Datatypes
Probability for Data Science Basic Concepts of Probability Axioms of Probability Conditional Probability
Central Tendencies for Continuous Variables Spread of Data KDE plots for Continuous Variable Overview of Distribution for Continuous variables Normal Distribution Skewed Distribution Skeweness and Kurtosis Distribution for Continuous Variable
Central Tendencies for Categorical Variables Understanding Discrete Distributions Performing EDA on Categorical Variables
Dealing with Missing Values Understanding Outliers Identifying Outliers in Data Outlier Detection in Python Outliers Detection Using IQR, Z-score, LOF and DBSCAN
Sample and Population Central Limit Theorem Confidence Interval and Margin of Error
Bivariate Analysis Introduction
Covariance Pearson Correlation Spearman's Correlation & Kendall's Tau Correlation versus Causation Tabular and Graphical methods for Bivariate Analysis Performing Bivariate Analysis on Continuous-Continuous Variables
Tabular and Graphical methods for Continuous-Categorical Variables Introduction to Hypothesis Testing P-value Two sample Z-test T-test T-test vs Z-test Performing Bivariate Analysis on Continuous-Catagorical variables
Chi-Squares Test Bivariate Analysis on Categorical Categorical Variables
Multivariate Analysis A Comprehensive Guide to Data Exploration The Data Science behind IPL
Supervised Learning vs Unsupervised Learning Reinforcement Learning Generative and Descriminative Models Parametric and Non Parametric model
Machine Learning Pipeline Preparing Dataset Build a Benchmark Model: Regression Build a Benchmark Model: Classification
Evaluation Metrics for Machine Learning Everyone should know Confusion Matrix Accuracy Precision and Recall AUC-ROC Log Loss R2 and Adjusted R2
Dealing with Missing Values Replacing Missing Values Imputing Missing Values in Data Working with Categorical Variables Working with Outliers Preprocessing Data for Model Building
Understanding Cost Function Understanding Gradient Descent Math Behind Gradient Descent Assumptions of Linear Regression Implement Linear Regression from Scratch Train Linear Regression in Python Implementing Linear Regression in R Diagnosing Residual Plots in Linear Regression Models Generalized Linear Models Introduction to Logistic Regression Odds Ratio Implementing Logistic Regression from Scratch Introduction to Scikit-learn in Python Train Logistic Regression in python Multiclass using Logistic Regression How to use Multinomial and Ordinal Logistic Regression in R ? Challenges with Linear Regression Introduction to Regularisation Implementing Regularisation Ridge Regression Lasso Regression
Introduction to K Nearest Neighbours Determining the Right Value of K in KNN Implement KNN from Scratch Implement KNN in Python
Bias Variance Tradeoff Introduction to Overfitting and Underfitting Visualizing Overfitting and Underfitting Selecting the Right Model What is Validation? Hold-Out Validation Understanding K Fold Cross Validation
Introduction to Feature Selection Feature Selection Algorithms Missing Value Ratio Low Variance Filter High Correlation Filter Backward Feature Elimination Forward Feature Selection Implement Feature Selection in Python Implement Feature Selection in R
Introduction to Decision Tree Purity in Decision Tree Terminologies Related to Decision Tree How to Select Best Split Point in Decision Tree? Chi-Squares Information Gain Reduction in Variance Optimizing Performance of Decision Tree Train Decision Tree using Scikit Learn Pruning of Decision Trees
Introduction to Feature Engineering Feature Transformation Feature Scaling Feature Engineering Frequency Encoding Automated Feature Engineering: Feature Tools
Introduction to Naive Bayes Conditional Probability and Bayes Theorem Introduction to Bayesian Adjustment Rating: The Incredible Concept Behind Online Ratings! Working of Naive Bayes Math behind Naive Bayes Types of Naive Bayes Implementation of Naive Bayes
Understanding how to solve Multiclass and Multilabled Classification Problem Evaluation Metrics: Multi Class Classification
Introduction to Ensemble Techniques Basic Ensemble Techniques Implementing Basic Ensemble Techniques Finding Optimal Weights of Ensemble Learner using Neural Network Why Ensemble Models Work well?
Introduction to Stacking Implementing Stacking Variants of Stacking Implementing Variants of Stacking Introduction to Blending Bootstrap Sampling Introduction to Random Sampling Hyper-parameters of Random Forest Implementing Random Forest Out-of-Bag (OOB) Score in the Random Forest IPL Team Win Prediction Project Using Machine Learning Introduction to Boosting Gradient Boosting Algorithm Math behind GBM Implementing GBM in python Regularized Greedy Forests Extreme Gradient Boosting Implementing XGBM in python Tuning Hyperparameters of XGBoost in Python Implement XGBM in R/H2O Adaptive Boosting Implementing Adaptive Boosing LightGBM Implementing LightGBM in Python Catboost Implementing Catboost in Python
Different Hyperparameter Tuning methods Implementing Different Hyperparameter Tuning methods GridsearchCV RandomizedsearchCV Bayesian Optimization for Hyperparameter Tuning Hyperopt
Understanding SVM Algorithm SVM Kernels In-depth Intuition and Practical Implementation SVM Kernel Tricks Kernels and Hyperparameters in SVM Implementing SVM from Scratch in Python and R
Introduction to Principal Component Analysis Steps to Perform Principal Compound Analysis Computation of Covariance Matrix Finding Eigenvectors and Eigenvalues Implementing PCA in python Visualizing PCA A Brief Introduction to Linear Discriminant Analysis Introduction to Factor Analysis
Introduction to Clustering Applications of Clustering Evaluation Metrics for Clustering Understanding K-Means Implementation of K-Means in Python Implementation of K-Means in R Choosing Right Value for K Profiling Market Segments using K-Means Clustering Hierarchical Clustering Implementation of Hierarchial Clustering DBSCAN Defining Similarity between clusters Build Better and Accurate Clusters with Gaussian Mixture Models
Understand Basics of Recommendation Engine with Case Study
8 Ways to Improve Accuracy of Machine Learning Models
Introduction to Dask Working with CuML
Introduction to Machine Learning Interpretability Framework and Interpretable Models model Agnostic Methods for Interpretability Implementing Interpretable Model Understanding SHAP Out-of-Core ML Introduction to Interpretable Machine Learning Models Model Agnostic Methods for Interpretability Game Theory & Shapley Values
Introduction to Machine Learning Interpretability Framework and Interpretable Models model Agnostic Methods for Interpretability Implementing Interpretable Model Understanding SHAP Out-of-Core ML Introduction to Interpretable Machine Learning Models Model Agnostic Methods for Interpretability Game Theory & Shapley Values
Introduction to AutoML Implementation of MLBox Introduction to PyCaret TPOT Auto-Sklearn EvalML
Pickle and Joblib Introduction to Model Deployment
Deploying Machine Learning Model using Streamlit Deploying ML Models in Docker Deploy Using Streamlit Deploy on Heroku Deploy Using Netlify Introduction to Amazon Sagemaker Setting up Amazon SageMaker Using SageMaker Endpoint to Generate Inference Deploy on Microsoft Azure Cloud Introduction to Flask for Model Deploying ML model using Flask
Model Deployment in Android Model Deployment in Iphone

Normal Distribution : An Ultimate Guide

Aashi
Aashi Last Updated : 08 Jun, 2021
6 min read

This article was published as a part of the Data Science Blogathon

Introduction

The normal distribution is an important class of Statistical Distribution that has a wide range of applications. This distribution applies in most Machine Learning Algorithms and the concept of the Normal Distribution is a must for any Statistician, Machine Learning Engineer, and Data Scientist.

So, In this article, we will explore all the concepts about Normal Distribution in a detailed manner.

Table of Contents

1. What is the Normal distribution?

2. Why is Normal Distribution Important?

3. Parameters of Normal Distribution

  • Mean
  • Standard Deviation

4. Properties of Normal Distribution

  • Symmetricity
  • Measures of Central Tendencies are equal
  • Empirical Rule
  • Skewness and Kurtosis
  • The area under the curve

5. Distributions Functions for the Normal Curve

  • Probability Density function (PDF)
  • Cumulative Density Function (CDF)

6. Applications of Normal Distribution

What is Normal Distribution?

The Normal distribution is also known as Gaussian or Gauss distribution. Many groups follow this type of pattern. That’s why it’s widely used in business, statistics, and in government bodies like the FDA:

  • Heights of people.
  • Measurement errors.
  • Blood pressure.
  • Points on a test.
  • IQ scores.
  • Salaries.

Let’s understand the concept with the help of the following example:

For Example,

The Normal distribution curve is seen in some of the competitive tests like the SAT, UPSC, JEE-Advanced, and GRE, etc. Here the normal distribution indicated that the bulk of students will score the average marks (grade=C), while smaller numbers of students will score the grades (B or D), and a smaller number of students score an F or an A grade.

All these types of inferences are taken from the empirical formula of Normal Distribution, which we will discuss later in this article.

Why is Normal Distribution Important?

There are several reasons why the normal distribution is crucial in statistics. Some of those are as follows:

1. The statistical hypothesis test assumes that the data follows a normal distribution.

2. Both linear and non-linear regression assumes that the residual follows the normal distribution.

3. Moreover, the central limit theorem states that as the sample size increases the distribution of the mean follows normal distribution irrespective of the distribution of the original variable

4. Apart from this most of the statistical software programs support some of the probability functions for normal distribution as well.

 

Parameters of Normal Distribution

There are two main parameters of a normal distribution- the mean and standard deviation. With the help of these parameters, we can decide the shape and probabilities of the distribution wrt our problem statement. As the parameter value changes, the shape of the distribution changes.

1. Mean

  • Researchers used the mean or average value as a measure of central tendency. It can be used to describe the distribution of variables that are measured as ratios or intervals.
  • The mean determines the location of the peak, and most of the data points are clustered around the mean in a normal distribution graph.
  • If we change the value of the mean, then the curve of normal distribution moves either to the left or right along the X-axis.

Normal distribution | means and standard deviation

Image Source: Google Images

 

2. Standard Deviation

  • The standard deviation measures how the data points are dispersed relative to the mean.
  • It determines how far the data points are away from the mean and represents the distance between the mean and the data points.
  • The standard deviation defines the width of the graph. As a result, changing the value of standard deviation tightens or expands the width of the distribution along the x-axis.
  • Usually, a smaller standard deviation wrt to the mean results in a steep curve while a larger standard deviation results in a flatter curve.

Normal distribution | same means- different distribution

Image Source: Google Images

 

Properties of Normal Distribution

All forms of the normal distribution share the following characteristics:

1. It is symmetric

  • The shape of the normal distribution is perfectly symmetrical.
  • This means that the curve of the normal distribution can be divided from the middle and we can produce two equal halves. Moreover, the symmetric shape exists when an equal number of observations lie on each side of the curve.

2. The mean, median, and mode are equal

  • The midpoint of normal distribution refers to the point with maximum frequency i.e., it consists of most observations of the variable.
  • The midpoint is also the point where all three measures of central tendency fall. These measures are usually equal in a perfectly shaped normal distribution.

3. Empirical rule

  • In normally distributed data, there is a constant proportion of data points lying under the curve between the mean and a specific number of standard deviations from the mean.
  • Thus, for a normal distribution, almost all values lie within 3 standard deviations of the mean.
  • These check buttons of normal distribution will help you realize the appropriate percentages of the area under the curve.
  • Remember that this empirical rule applies to all normal distributions. Also, note that these rules are applied only to the normal distributions.

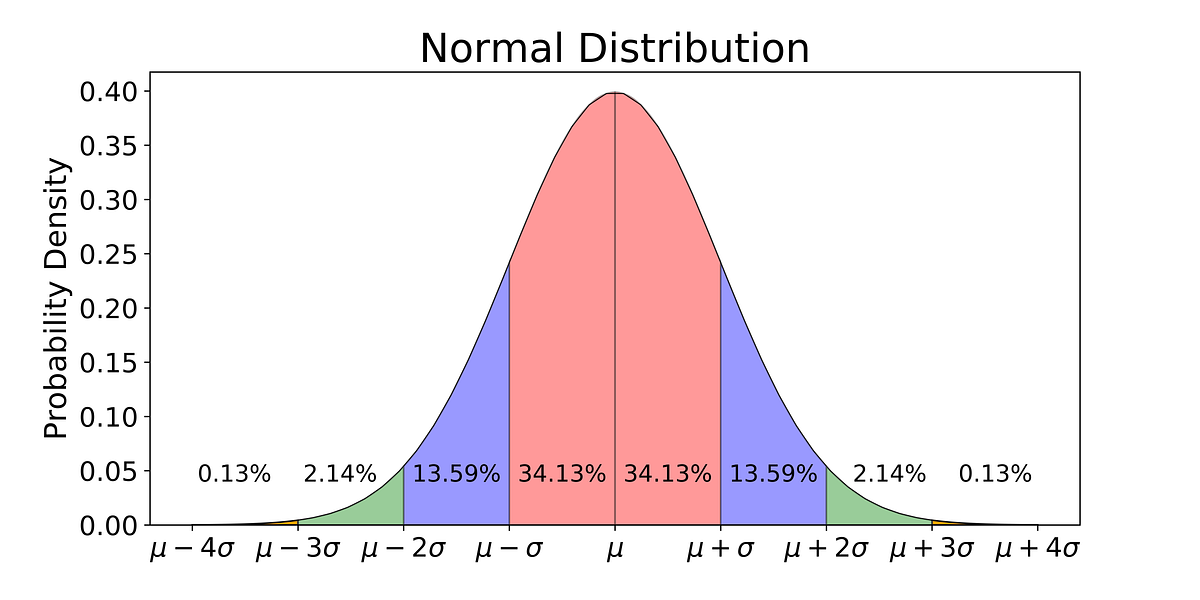
Explaining the 68-95-99.7 rule for a Normal Distribution | by Michael Galarnyk | Towards Data Science

Fig. Empirical Formula of Normal Distribution

Image Source: Google Images

4. Skewness and kurtosis

  • Skewness and kurtosis are coefficients that measure how different the distribution is from a normal distribution.
  • It measures the symmetry of the normal distribution while kurtosis measures the thickness of the tail distribution relative to that of normal distribution.

5. Area under the curve

  • The total area under the curve is unity(=1)

Distributions Functions for the Normal Curve

1. Probability Density Function (PDF)

The general formula for the probability density function of the normal distribution is given by,

distribution function | Normal distribution

where,

μ is the location parameter, and

σ is the scale parameter

2. Cumulative Density Function (CDF)

The formula for the cumulative distribution function of the normal distribution is given by,

CDF | Normal distribution

Remember that the above integral does not exist in a simple closed formula. It is computed numerically.

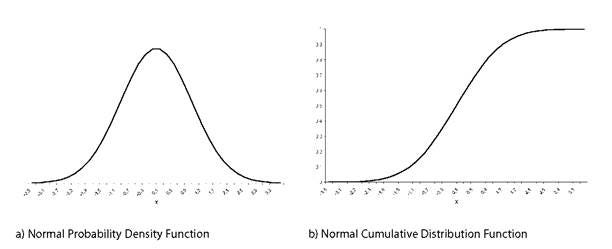
Machine Learning Primal: Normal Distribution | by Mihir Parulekar | Medium

Fig. PDF and CDF for Normal Distribution

Image Source: Google Images

 

Special Case:

The case where μ = 0 and σ = 1 is called the standard normal distribution. The equations for the standard normal distribution is

pdf and cdf

Fig. PDF of Standard Normal Distribution

Applications of Normal Distribution

Let us apply the Empirical Rule to the following problem:

Problem Statement: 

Let’s have data of heights of Indian women aged 18 to 24, which is approximately normally distributed with a mean of 65.5 inches and a standard deviation of 2.5 inches.

From the empirical rule, it follows that:

– 68% of these Indian women have heights between 65.5 – 2.5 and 65.5 + 2.5 inches or between 63 and 68 inches,

– 95% of these Indian women have heights between 65.5 – 2(2.5) and 65.5 + 2(2.5) inches, or between 60.5 and 70.5 inches.

– Therefore, the tallest 2.5% of these women are taller than 70.5 inches. (The extreme 5% fall more than two standard deviations, or 5 inches from the mean. And since all normal distributions are symmetric about their mean, half of these women are on the tall side.)

– Almost all young Indian women are between 58 and 73 inches in height if you use the 99.7% calculations.

Endnotes

Thanks for reading!

I hope you enjoyed the article and increased your knowledge about Normal Distribution in Statistics.

Please feel free to contact me on Email

Something not mentioned or want to share your thoughts? Feel free to comment below And I’ll get back to you.

About the Author

Aashi Goyal

Currently, I am pursuing my Bachelor of Technology (B.Tech) in Electronics and Communication Engineering from Guru Jambheshwar University(GJU), Hisar. I am very enthusiastic about Statistics, Machine Learning and Deep Learning.

The media shown in this article are not owned by Analytics Vidhya and are used at the Author’s discretion.

Aashi
Aashi

Currently, I am pursuing my Bachelor of Technology (B.Tech) in Electronics and Communication Engineering from Guru Jambheshwar University(GJU), Hisar. I am very enthusiastic about Statistics, Machine Learning and Deep Learning.

Free Courses

Generative AI 4.7

Generative AI - A Way of Life

Explore Generative AI for beginners: create text and images, use top AI tools, learn practical skills, and ethics.
Large Language Models 4.5

Getting Started with Large Language Models

Master Large Language Models (LLMs) with this course, offering clear guidance in NLP and model training made simple.
Prompt Engineering 4.6

Building LLM Applications using Prompt Engineering

This free course guides you on building LLM apps, mastering prompt engineering, and developing chatbots with enterprise data.
LlamaIndex 4.8

Improving Real World RAG Systems: Key Challenges & Practical Solutions

Explore practical solutions, advanced retrieval strategies, and agentic RAG systems to improve context, relevance, and accuracy in AI-driven applications.
RAG systems using LlamaIndex 4.7

Microsoft Excel: Formulas & Functions

Master MS Excel for data analysis with key formulas, functions, and LookUp tools in this comprehensive course.

Recommended Articles

Responses From Readers

Clear

Write for us

Write, captivate, and earn accolades and rewards for your work
  • Reach a Global Audience
  • Get Expert Feedback
  • Build Your Brand & Audience
  • Cash In on Your Knowledge
  • Join a Thriving Community
  • Level Up Your Data Science Game
imag

We use cookies essential for this site to function well. Please click to help us improve its usefulness with additional cookies. Learn about our use of cookies in our Privacy Policy & Cookies Policy.

Show details