Top 15 Questions to Test your Data Science Skills on SVM

CHIRAG GOYAL 22 Jun, 2022 • 6 min read

This article was published as a part of the Data Science Blogathon

Introduction

Before the sudden rise of neural networks, Support Vector Machines (SVMs) was considered the most powerful Machine Learning Algorithm. Still, it is more computation friendly as compared to Neural Networks and used extensively in industries. In this article, we will discuss the most important questions on SVM that are helpful to get you a clear understanding of the SVMs and also for Data Science Interviews, which covers its very fundamental level to complex concepts.

Let’s get started,

1. What are Support Vector Machines (SVMs)?

👉 SVM is a supervised machine learning algorithm that works on both classification and regression problem statements.

👉 For classification problem statements, it tries to differentiate data points of different classes by finding a hyperplane that maximizes the margin between the classes in the training data.

👉 In simple words, SVM tries to choose the hyperplane which separates the data points as widely as possible since this margin maximization improves the model’s accuracy on the test or the unseen data.

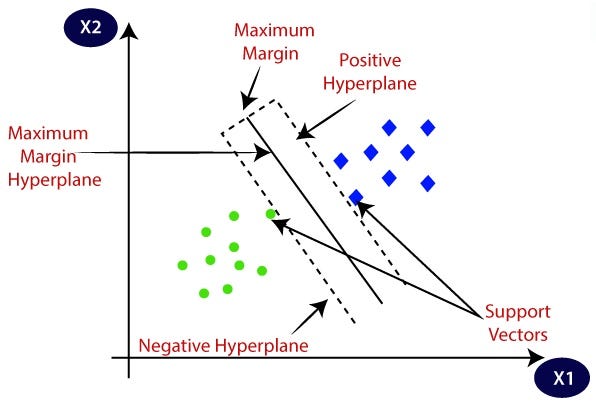
Everything one should know about — Support Vector Machines (SVM) | by Aman Kapri | Analytics Vidhya | Medium

Image Source: link

2. What are Support Vectors in SVMs?

👉 Support vectors are those instances that are located on the margin itself. For SVMS, the decision boundary is entirely determined by using only the support vectors.

👉 Any instance that is not a support vector (not on the margin boundaries) has no influence whatsoever; you could remove them or add more instances, or move them around, and as long as they stay off the margin they won’t affect the decision boundary.

👉 For computing the predictions, only the support vectors are involved, not the whole training set.

3. What is the basic principle of a Support Vector Machine?

It’s aimed at finding an optimal hyperplane that is linearly separable, and for the dataset which is not directly linearly separable, it extends its formulation by transforming the original data to map into a new space, which is also called kernel trick.

4. What are hard margin and soft Margin SVMs?

👉 Hard margin SVMs work only if the data is linearly separable and these types of SVMs are quite sensitive to the outliers.👉 But our main objective is to find a good balance between keeping the margins as large as possible and limiting the margin violation i.e. instances that end up in the middle of margin or even on the wrong side, and this method is called soft margin SVM.

5. What do you mean by Hinge loss?

The function defined by max(0, 1 – t) is called the hinge loss function.

A definitive explanation to the Hinge Loss for Support Vector Machines. | by Vagif Aliyev | Towards Data Science

Image Source: link

Properties of Hinge loss function:

👉 It is equal to 0 when the value of t is greater than or equal to 1 i.e, t>=1.

👉 Its derivative (slope) is equal to –1 if t < 1 and 0 if t > 1.

👉 It is not differentiable at t = 1.

👉 It penalizes the model for wrongly classifying the instances and increases as far the instance is classified from the correct region of classification.

6. What is the “Kernel trick”?

👉 A Kernel is a function capable of computing the dot product of instances mapped in higher dimension space without actually transforming all the instances into the higher feature space and calculating the dot product.👉 This trick makes the whole process much less computationally expensive than that actual transformation to calculate the dot product and this is the essence of the kernel trick.

11 Support Vector Machine ideas | machine learning, supportive, handwriting recognition

Image Source: link

7. What is the role of the C hyper-parameter in SVM? Does it affect the bias/variance trade-off?

👉 The balance between keeping the margins as large as possible and limiting the margin violation is controlled by the C parameter: a small value leads to a wider street but more margin violation and a higher value of C makes fewer margin violations but ends up with a smaller margin and overfitting.👉 Here thing becomes a little complex as we have conflicting objectives of making the slack variables as small as possible to reduce margin violation and make W as small as possible to increase the margin. This is where the role of the C hyperparameter comes in which allows us to define the trade-off between these two objectives.

8. Explain different types of kernel functions.

A function is called kernel if there exist a function ϕ that maps a and b into another space such that K(a, b) = ϕ(a)^T · ϕ(b). So you can use K as a kernel since you just know that a mapping ϕ exists, even if you don’t know what ϕ function is. These are the very good things about kernels.

Some of the kernel functions are as follows:

👉 Polynomial Kernel: These are the kernel functions that represent the similarity of vectors in a feature space over polynomials of original variables.

👉 Gaussian Radial Basis Function (RBF) kernel: Gaussian RBF kernel maps each training instance to an infinite-dimensional space, therefore it’s a good thing that you don’t need to perform the mapping.

TWO COMMON KERNELS FUNCTIONS | Download Table

Image Source: link

9. How you formulate SVM for a regression problem statement?

For formulating SVM as a regression problem statement we have to reverse the objective: instead of trying to fit the largest possible street between two classes which we will do for classification problem statements while limiting margin violations, now for SVM Regression, it tries to fit as many instances as possible between the margin while limiting the margin violations.

10. What affects the decision boundary in SVM?

Adding more instances off the margin of the hyperplane does not affect the decision boundary, it is fully determined (or supported ) by the instances located at the edge of the street called support vectors

11. What is a slack variable?

👉 To meet the soft margin objective, we need to introduce a slack variable ε>=0 for each sample; it measures how much any particular instance is allowed to violate the margin.👉 Here thing becomes little complex as we have conflicting objectives of making the slack variables as small as possible to reduce margin violation and make w (weight matrix) as small as possible to increase the margin. This is where the role of the C hyperparameter comes which allows us to define the trade-off between these two objectives.

Fig. Picture Showing the slack variables

Image Source: link

12. What is a dual and primal problem and how is it relevant to SVMs?

👉 Given a constrained optimization problem, known as the Primal problem, it is possible to express a different but closely related problem, which is known as its Dual problem.👉 The solution to the dual problem typically provides a lower bound to the solution of the primal problem, but under some conditions, it can be possible that it has even the same solutions as the primal problem.

👉 Fortunately, the SVM problem completes these conditions, so that you can choose to solve the primal problem or the dual problem; and they both will have the same solution.

13. Can an SVM classifier outputs a confidence score when it classifies an instance? What about a probability?

👉 An SVM classifier can give the distance between the test instance and the decision boundary as output, so we can use that as a confidence score, but we cannot use this score to directly converted it into class probabilities.👉 But if you set probability=True when building a model of SVM in Scikit-Learn, then after training it will calibrate the probabilities using Logistic Regression on the SVM’s scores. By using this techniques, we can add the predict_proba() and predict_log_proba() methods to the SVM model.

14. If you train an SVM classifier with an RBF kernel. It seems to underfit the training dataset: should you increase or decrease the hyper-parameter γ (gamma)? What about the C hyper-parameter?

If we trained an SVM classifier using a Radial Basis Function (RBF) kernel, then it underfits the training set, so there might be too much regularization. To decrease it, you need to increase the gamma or C hyper-parameter.

15. Is SVM sensitive to the Feature Scaling?

Yes, SVMs are sensitive to feature scaling as it takes input data to find the margins around hyperplanes and gets biased for the variance in high values.

End Notes

Thanks for reading!
I hope you enjoyed the questions and were able to test your knowledge about Support Vector Machines (SVM).

If you liked this and want to know more, go visit my other articles on Data Science and Machine Learning by clicking on the Link

Please feel free to contact me on Linkedin, Email.

Something not mentioned or want to share your thoughts? Feel free to comment below And I’ll get back to you.

About the author

Chirag Goyal

Currently, I pursuing my Bachelor of Technology (B.Tech) in Computer Science and Engineering from the Indian Institute of Technology Jodhpur(IITJ). I am very enthusiastic about Machine learning, Deep Learning, and Artificial Intelligence.

The media shown in this article are not owned by Analytics Vidhya and is used at the Author’s discretion.

CHIRAG GOYAL 22 Jun 2022

I am currently pursuing my Bachelor of Technology (B.Tech) in Computer Science and Engineering from the Indian Institute of Technology Jodhpur(IITJ). I am very enthusiastic about Machine learning, Deep Learning, and Artificial Intelligence. Feel free to connect with me on Linkedin.

Algorithm Beginner Data Science Listicle

Top 15 Questions to Test your Data Science Skills on SVM

Introduction

Let’s get started,

1. What are Support Vector Machines (SVMs)?

2. What are Support Vectors in SVMs?

3. What is the basic principle of a Support Vector Machine?

4. What are hard margin and soft Margin SVMs?

5. What do you mean by Hinge loss?

6. What is the “Kernel trick”?

7. What is the role of the C hyper-parameter in SVM? Does it affect the bias/variance trade-off?

8. Explain different types of kernel functions.

9. How you formulate SVM for a regression problem statement?

10. What affects the decision boundary in SVM?

11. What is a slack variable?

12. What is a dual and primal problem and how is it relevant to SVMs?

13. Can an SVM classifier outputs a confidence score when it classifies an instance? What about a probability?

14. If you train an SVM classifier with an RBF kernel. It seems to underfit the training dataset: should you increase or decrease the hyper-parameter γ (gamma)? What about the C hyper-parameter?

15. Is SVM sensitive to the Feature Scaling?

End Notes

About the author

Chirag Goyal

Frequently Asked Questions

Responses From Readers

Related Courses

Top Data Science Projects for Analysts and Data Scientists

Free

Write for us