This article was published as a part of the Data Science Blogathon
Introduction
Hierarchical Clustering is one of the most popular and useful clustering algorithms. It can be used as an alternative for partitioned clustering as there is no requirement of pre-specifying the number of clusters to be created.
Therefore it becomes necessary for every aspiring Data Scientist and Machine Learning Engineer to have a good knowledge of the Hierarchical Clustering Algorithm.
In this article, we will discuss the most important questions on the Hierarchical Clustering Algorithm which is helpful to get you a clear understanding of the Algorithm, and also for Data Science Interviews, which covers its very fundamental level to complex concepts.
Let’s get started,
1. What do you mean by Clustering?
Clustering is an unsupervised machine learning technique that groups similar observations in a cluster(group of similar observations) such that the observations in the same group are more similar to each other than the observations in the other groups i.e observations in different clusters are dissimilar to each other.
Image Source: Google Images
2. What is a Hierarchical Clustering Algorithm?
Hierarchical Clustering i.e, an unsupervised machine learning algorithm is used to group the unlabeled datasets into a single group, named, a cluster. Sometimes, it is also known as Hierarchical cluster analysis (HCA).
In this algorithm, we try to create the hierarchy of clusters in the form of a tree, and this tree-shaped structure is known as the Dendrogram.
3. What are the various types of Hierarchical Clustering?
The two different types of Hierarchical Clustering technique are as follows:
Agglomerative: It is a bottom-up approach, in which the algorithm starts with taking all data points as single clusters and merging them until one cluster is left.
Divisive: It is just the opposite of the agglomerative algorithm as it is a top-down approach.
Image Source: Google Images
4. Explain the Agglomerative Hierarchical Clustering algorithm with the help of an example.
Initially, each data point is considered as an individual cluster in this technique. After each iteration, the similar clusters merge with other clusters and the merging will stop until one cluster or K clusters are formed.The steps of the agglomerative algorithm are as follows:
- Compute the proximity matrix.
- Let each data point be a cluster.
- Repeat this step: Combine the two closest clusters and accordingly update the proximity matrix.
- Until only a single cluster remains.
For Example,
Let’s say we have six observations named {A,B,C,D,E,F}.
Step- 1: In the first step, we compute the proximity of individual observations and consider all the six observations as individual clusters.
Step- 2: In this step, similar clusters are merged together and result in a single cluster.
For our example, we consider B, C, and D, E are similar clusters that are merged in this step. Now, we are remaining with four clusters named A, BC, DE, F.
Step- 3: We again compute the proximity of new clusters and merge the similar clusters to form new clusters A, BC, DEF.
Step- 4: Again, compute the proximity of the newly formed clusters. Now, the clusters named DEF and BC are similar and combine together to form a new cluster. Therefore, now we are left with two clusters named A, BCDEF.
Step- 5: Finally, all the clusters are combined together and form a single cluster and our procedure is completed for the given algorithm.
Therefore, the pictorial representation of the above example is shown below:
5. Describe the Divisive Hierarchical Clustering Algorithm in detail.
In simple words, Divisive Hierarchical Clustering is working in exactly the opposite way as Agglomerative Hierarchical Clustering. In Divisive Hierarchical Clustering, we consider all the data points as a single cluster, and after each iteration, we separate the data points from the cluster which are not similar. Each data point that is separated is considered as an individual cluster. Finally, we’ll be remaining with n number of clusters.Since we’re dividing the single clusters into n clusters, it is named Divisive Hierarchical Clustering. This technique is not much used in real-world applications.
6. Explain the different linkage methods used in the Hierarchical Clustering Algorithm.
The popular linkage methods used in Hierarchical Clustering are as follows:Complete-linkage: In this method, the distance between two clusters is defined as the maximum distance between two data points from each cluster.
Single-linkage: In this method, the distance between two clusters is defined as the minimum distance between two data points in each cluster.
Average-linkage: In this method, the distance between two clusters is defined as the average distance between each data point in one cluster to every data point in the other cluster.
Centroid-linkage: In this method, we find the centroid of cluster 1 and the centroid of cluster 2 and then calculate the distance between the two before merging.
7. List down the pros and cons of complete and single linkages methods in the Hierarchical Clustering Algorithm.
Pros of Single-linkage:
- This approach can differentiate between non-elliptical shapes as long as the gap between the two clusters is not small.
Cons of Single-linkage:
- This approach cannot separate clusters properly if there is noise between clusters.
Pros of Complete-linkage:
- This approach gives well-separating clusters if there is some kind of noise present between clusters.
Cons of Complete-Linkage:
- This approach is biased towards globular clusters.
- It tends to break large clusters.
8. What is the group average method for calculating the similarity between two clusters for the Hierarchical Clustering Algorithm?
In the group average method, we take all the pairs of data points and calculate their similarities and find the average of all the similarities.Mathematically this can be written as,
sim(C1, C2) = ∑ sim(Pi, Pj)/|C1|*|C2|
where Pi ∈ C1 & Pj ∈ C2
Image Source: Google Images
Pros of Group Average:
- This approach does well in separating clusters if there is noise present between the clusters.
Cons of Group Average:
- This approach is biased towards globular clusters.
9. Explain Ward’s method for calculating the similarity between two clusters in the Hierarchical Clustering Algorithm.
In this method, we find the similarity between clusters by calculating the sum of the square of the distances Pi and Pj.Mathematically this can be written as,
sim(C1, C2) = ∑ (dist(Pi, Pj))²/|C1|*|C2|
Pros of Ward’s method:
- This approach also does well in separating clusters if there are some of the noisy points or outliers present between the clusters.
Cons of Ward’s method:
- This approach is biased towards globular clusters.
10. What is a dendrogram in Hierarchical Clustering Algorithm?
A dendrogram is defined as a tree-like structure that is mainly used to store each step as a memory that the Hierarchical clustering algorithm performs. In the dendrogram plot, the Y-axis represents the Euclidean distances between the observations, and the X-axis represents all the observations present in the given dataset.
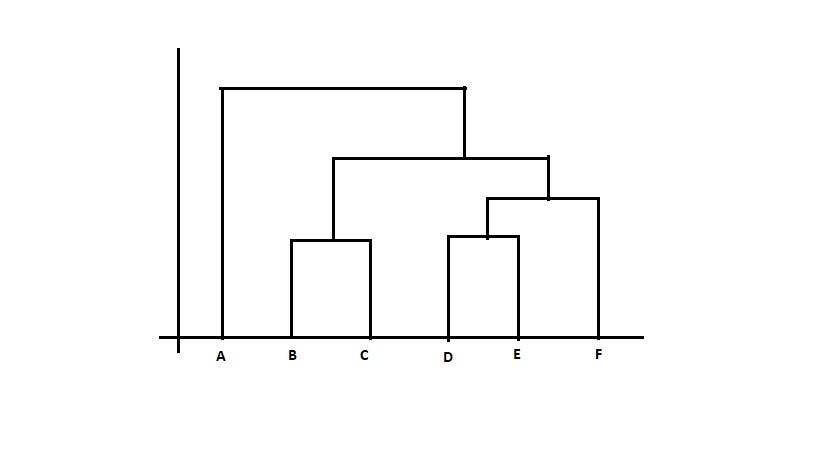
Image Source: Google Images
Please read the Wikipedia article for a better understanding of Dendrogram:
11. Explain the working of dendrogram in the agglomerative Hierarchical Clustering Algorithm.
The working of the dendrogram can be easily understood using the given below diagram:
Image Source: Google Images
In the above diagram, the left part is showing how clusters are formed during the execution of the agglomerative clustering algorithm, and the right part is showing the corresponding dendrogram formed.
Step by step working of the algorithm:
Step-1: Firstly, the data points P2 and P3 merged together and form a cluster, correspondingly a dendrogram is created, which connects P2 and P3 with a rectangular shape. The height is decided according to the Euclidean distance between the data points.
Step-2: In the next step, P5 and P6 form a cluster, and the corresponding dendrogram is created. It is higher than the previous, as the Euclidean distance between P5 and P6 is a little bit greater than the P2 and P3.
Step-3: Again, two new dendrograms are formed that combine P1, P2, and P3 in one dendrogram, and P4, P5, and P6, in another dendrogram.
Step-4: At last, the final dendrogram is formed that combines all the data points together.
Note: As per our requirement according to the problem statement, we can cut the dendrogram at any level.
12. Explain the different parts of dendrograms in the Hierarchical Clustering Algorithm.
Image Source: Google Images
A dendrogram can be understood as a column graph or a row graph. Some dendrograms are circular or have a fluid shape, but the software will usually produce a row or column graph. No matter what the shape, the basic graph consists of the following same parts:
- For arranging the Clades (branch), take the help of how similar (or dissimilar) they are. Clades that are having or close to the same height are similar to each other; whereas clades with different heights are dissimilar from each other, which implies that the more the value of the difference in height, the more will be dissimilar.
- Each clade has one or more leaves.
Now for the given diagram, we have:
- Leaves A, B, and C are more similar to each other than they are to leaves D, E, or F.
- Leaves D and E are more similar to each other than they are to leaves A, B, C, or F.
- Leaf F is substantially different from all of the other leaves due to different heights in the dendrogram.
Theoretically, a clade can have an infinite amount of leaves but the more leaves we have, the harder the dendrogram will be to read and understand with the help of naked eyes.
13. How can you find the clusters to have upon looking at the dendrogram?
In a dendrogram, look for the largest vertical line which doesn’t cross any horizontal line.With the help of this line, we can draw a horizontal line and then, the points where this horizontal line cross over the various vertical lines, we count all those intersecting points, and then count of intersecting points is the ideal answer for the number of clusters the dataset can have.
14. What is Space and Time Complexity of the Hierarchical Clustering Algorithm?
Space complexity: Hierarchical Clustering Technique requires very high space when the number of observations in our dataset is more since we need to store the similarity matrix in the RAM. So, the space complexity is the order of the square of n.Space complexity = O(n²) where n is the number of observations.
Time complexity: Since we have to perform n iterations and in each iteration, we need to update the proximity matrix and also restore that matrix, therefore the time complexity is also very high. So, the time complexity is the order of the cube of n.
Time complexity = O(n³) where n is the number of observations.
15. List down some of the possible conditions for producing two different dendrograms using an agglomerative Clustering algorithm with the same dataset.
The given situation happens due to either of the following reasons:
- Change in Proximity function
- Change in the number of data points or variables.
These changes will lead to different Clustering results and hence different dendrograms.
16. For the dendrogram given below, find the most appropriate number of clusters for the data points of the given dataset.
To take the decision for the number of clusters that can best depict different clusters can be chosen by carefully observing the dendrogram formed during the algorithm run.
The best choice of the number of clusters is the number of vertical lines in the dendrogram intersect by a horizontal line that can transverse the maximum distance vertically without intersecting a cluster.
In the above example, the best choice of the number of clusters will be 4 since the red horizontal line in the dendrogram below covers the maximum vertical distance AB.
17. What are the conditions to stop combining the clusters in the Hierarchical Clustering Algorithm?
Some of the popular approaches to stop combining the clusters are as follows:
Approach 1: Pick several clusters(k) upfront
When we don’t want to form, for example, 250 clusters, then we choose the K value. Therefore, we decide the number of clusters (say, the first five or six) required in the beginning, and we complete the process when we reach the value K. This is done so that we can put a limit on the incoming information.
It becomes very important especially when we are feeding it into another algorithm that probably requires three or four values.
Possible challenges: This approach only makes sense when you know the data well or you have some domain knowledge when you’re clustering with K clusters. But if you’re analyzing a brand new dataset, then you may not know how many clusters we are required.
Approach 2: Stop combining the clusters when the next merging of clusters would form a cluster with low cohesion.
We keep clustering until the next combination of clusters gives a bad cluster with a low cohesion setup. This implies that the points are so close to being in both the clusters that it doesn’t make sense to keep them together.
Approach 3:
Approach 3.1: Diameter of a cluster
The diameter of a cluster is defined as the maximum distance between any pair of observations in the cluster.
We stop combining the clusters when the diameter of a new cluster formed exceeds the threshold. Moreover, we don’t want the two clusters to overlap as the diameter increases.
Approach 3.2: Radius of a cluster
The radius of a cluster is defined as the maximum distance of a point from the centroid.
We stop combining the clusters when the radius of a new cluster formed exceeds the threshold(decided by the user itself according to the problem statement).
18. How to Find the Optimal Number of Clusters in Agglomerative Clustering Algorithm?
To find the optimal number of clusters, Silhouette Score is considered to be one of the popular approaches. This technique measures how close each of the observations in a cluster is to the observation in its neighboring clusters.Let ai be the mean distance between an observation i and other observations in the cluster to which observation i assigned.
Let bi be the minimum mean distance between an observation i and observation in other clusters.
Conclusion:
- The range of the Silhouette Scores is from -1 to +1. Higher the value of the Silhouette Score indicates observations are well clustered.
- Silhouette Score = 1 describes that the data point (i) is correctly and well-matched in the cluster assignment.
19. How can we measure the goodness of the clusters in the Hierarchical Clustering Algorithm?
There are many measures to find the goodness of clusters but the most popular one is the Dunn’s Index. Dunn’s index is defined as the ratio of the minimum inter-cluster distances to the maximum intra-cluster diameter and the diameter of a cluster is calculated as the distance between its two furthermost points i.e, maximum distance from each other.
Conclusion:
- In order to have well separated and compact clusters, we should aim for a higher value of Dunn’s index.
Image Source: Google Images
20. What are the advantages and disadvantages of the Hierarchical Clustering Algorithm?
Advantages of Hierarchical Clustering:
- We can obtain the optimal number of clusters from the model itself, human intervention not required.
- Dendrograms help us in clear visualization, which is practical and easy to understand.
Disadvantages of Hierarchical Clustering:
- Not suitable for large datasets due to high time and space complexity.
- There is no mathematical objective for Hierarchical clustering.
- All the approaches to calculate the similarity between clusters has their own disadvantages.
End Notes
Thanks for reading!
I hope you enjoyed the questions and were able to test your knowledge about the Hierarchical Clustering Algorithm.
If you liked this and want to know more, go visit my other articles on Data Science and Machine Learning by clicking on the Link
Please feel free to contact me on Linkedin, Email.
Something not mentioned or want to share your thoughts? Feel free to comment below And I’ll get back to you.
About the author
Chirag Goyal
Currently, I am pursuing my Bachelor of Technology (B.Tech) in Computer Science and Engineering from the Indian Institute of Technology Jodhpur(IITJ). I am very enthusiastic about Machine learning, Deep Learning, and Artificial Intelligence.
The media shown in this article on Sign Language Recognition are not owned by Analytics Vidhya and are used at the Author’s discretion.
I am a B.Tech. student (Computer Science major) currently in the pre-final year of my undergrad. My interest lies in the field of Data Science and Machine Learning. I have been pursuing this interest and am eager to work more in these directions. I feel proud to share that I am one of the best students in my class who has a desire to learn many new things in my field.
