This article was published as a part of the Data Science Blogathon
Introduction
This article is part of an ongoing blog series on Natural Language Processing (NLP). In the previous article, we completed a basic technique of Topic Modeling named Non-Negative Matrix Factorization. So, In continuation of that part now we will start our discussion on another Topic modeling technique named Latent Semantic Analysis.
So, In this article, we will deep dive into a Topic Modeling technique named Latent Semantic Analysis (LSA) and see how this technique uncovers these latent topics which become a very useful thing while we work on any NLP Problem statement.
This is part-16 of the blog series on the Step by Step Guide to Natural Language Processing.
Table of Contents
1. Recap of Topic Modeling
2. Why do we need Latent Semantic Analysis (LSA)?
3. What is Latent Semantic Analysis (LSA)?
4. Steps involved while Implementing LSA
5. Advantages and Disadvantages of LSA
6. How to choose the Optimal number of Topics?
7. Applications of LSA
Recap of Topic Modeling
Basic assumptions on which all topic modeling algorithms are based:
- Each document consists of more than one topics, and
- Each topic consists of a collection of words.
In other words, topic modeling algorithms are built around the idea that the semantics of our document is actually being governed by some hidden, or “latent,” variables that we are not observing directly after seeing the textual material.
Image Source: Google Images
As a result, to uncover these latent variables which shape the meaning of our document and corpus, we require topic modeling algorithms. In the later part of this blog post, we will build up an understanding of how different topic models uncover these latent topics. But in this article, we will discuss the LSA technique first, and then as we go ahead we will also discuss different techniques of Topic modeling such as LDA, pLSA, etc.
Why do we need Latent Semantic Analysis?
As we discussed starting from the first article, we have discussed that all-natural languages have their own intricacies and nuances which are quite difficult for a machine to capture, and also sometimes they’re even misunderstood by us humans!. This involves different words that have the same thing, and also the words which have the same spelling but gives different meanings.
For Example, consider the following two sentences:
Sentences: I liked the last novel of Premchand quite a lot. They would like to go for a novel marketing campaign.
In the first sentence, the word ‘novel’ represents a book, while in the second sentence, it means new or fresh.
We as a human can easily differentiate between these two words since we can understand the context behind these two words. However, the machines would not be able to capture this concept as they cannot understand the context in which the words have been used. This is where the role of Latent Semantic Analysis (LSA) comes into the picture!
LSA tries to leverage the context around the words to capture the hidden or latent concepts, which are called topics.
So, if we simply mapped the words to documents, then it won’t really helpful for us. So, What we really require is to extract the hidden concepts or topics behind the words. LSA is one such technique that can be used to find these hidden topics which we will be discussing in this article.
What is Latent Semantic Analysis?
LSA, which stands for Latent Semantic Analysis, is one of the foundational techniques used in topic modeling. The core idea is to take a matrix of documents and terms and try to decompose it into separate two matrices –
- A document-topic matrix
- A topic-term matrix.
Therefore, the learning of LSA for latent topics includes matrix decomposition on the document-term matrix using Singular value decomposition. It is typically used as a dimension reduction or noise-reducing technique.
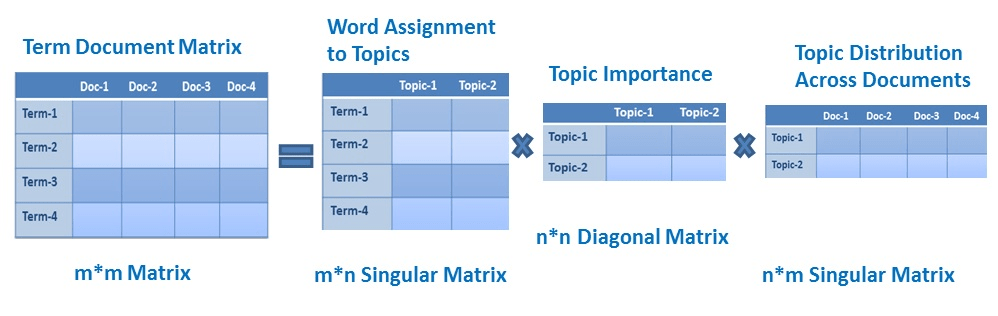
Image Source: Google Images
Steps Involved while Implementing LSA
Let’s say we have m number of text documents with n number of total unique words i.e, the number of words in your vocabulary. Our objective is to extract k topics from all the text data in the documents. The user has to specify the number of topics, k.
Step-1
The first step is to generate a document-term matrix of shape m x n in which each row represents a document and each column represents a word having some scores.

Image Source: Google Images
How Scores can be calculated?
For calculating the scores, we can use several methods such as:
1. We can fill each column entry simply by a raw count of the number of times the jth word appeared in the i-th document. But In practice, simply raw counts don’t work particularly well because they do not consider the significance of each word in the document.
2. Typically, LSA models replace raw counts in the document-term matrix with a TF-IDF score.
TF-IDF or Term frequency-Inverse document frequency assigns a weight for term j in document i with the help of the following formula:
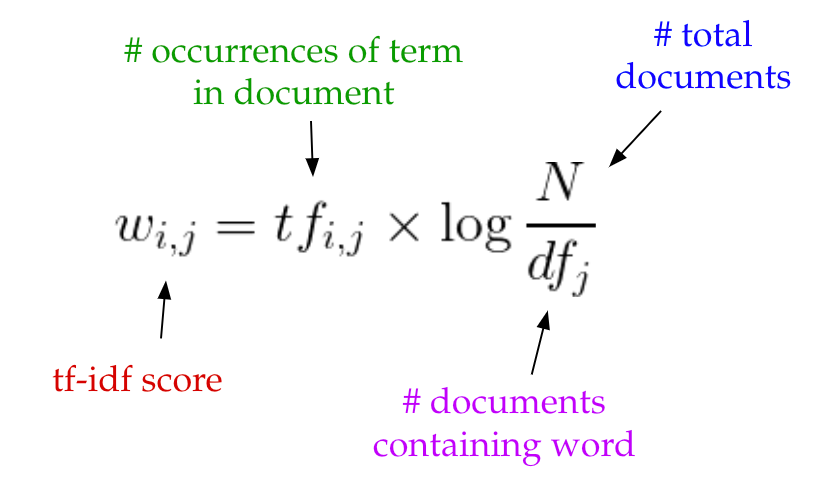
Image Source: Google Images
Intuitively, from the above formula, a term has given a large weight when that particular term occurs frequently across the document but infrequently across the corpus.
Step-2
Once we computed the document-term matrix A, we can start thinking about our latent or hidden topics present in the documents or corpus. Here’s we can observe that the document term matrix
- A is very sparse,
- A is noisy,
- A is redundant across its many dimensions.
As a result, to find the few latent topics that capture the relationships among the words and documents, we want to perform dimensionality reduction on document term matrix A.
Then, we have to reduce the dimensions of the above document term matrix to k, which specifies the number of desired topics) dimensions.
How we can perform Dimensionality Reduction?
This dimensionality reduction can be done using truncated Singular Value decomposition.
Singular Value Decomposition (SVD)
The idea of SVD is finding the most valuable information and using lower dimension t to represent the same thing. Singular Value Decomposition is a technique in linear algebra that factorizes any matrix A into the product of 3 separate matrices. It has many useful applications in many domains such as signal processing, psychology, sociology, climate, and atmospheric science, statistics, and astronomy. It decomposes the matrix into three different matrices:
- Orthogonal column matrix, (V)
- Orthogonal row matrix, (U)
- One singular matrix. (S)
M=U*S*V
where S is a diagonal matrix having diagonal elements as the singular values of A.
Critically, what truncated SVD does is reduce the dimensionality by choosing only the t largest singular values, and only keeping the first t columns of the matrix U and V. Here, t is a hyperparameter that we can select and adjust to reflect the number of topics we want to extract.

Intuitively, we can think of this as only keeping the t most significant dimensions in our transformed space.

In this case, the matrix U ∈ ℝ(m ⨉ k) becomes our document-topic matrix, and the matrix V ∈ ℝ(n ⨉ k) becomes our term-topic matrix. In both, the matrices U and V, the columns correspond to one of our t topics.
- U matrix: In this matrix, rows represent document vectors expressed in terms of topics.
- V matrix: In this matrix, rows represent term vectors expressed in terms of topics.
What do we get after applying SVD?
Each row of the matrix Uk (document-topic matrix) is the vector representation of the corresponding document. Here the length of these vectors is equal to k, which is the number of desired topics we want and vector representation for the terms in our data can be found in the matrix Vk (term-topic matrix).
So, SVD returns us vector representations for every document and term in our data. The length of each vector would be k. One important use of these vectors is we can find similar words and similar documents with the help of the cosine similarity metric.
Application of Document and Term Vectors
Now with the help of these document vectors and term vectors, we can easily calculate some measures such as cosine similarity to evaluate:
- The similarity of different documents.
- The similarity of different words.
- The similarity of terms or queries and documents which will become useful in information retrieval, when we want to retrieve passages most relevant to our search query.
Test Your Previous Knowledge
1. Suppose we have 10 documents in the training data, each of which contains 100 sentences. Each sentence contains at most 20 words. We are required to build a model classifying each sentence using this data. Which of the following represent the dimension of X_train?
- (1000, 20)
- (12000, 1)
- (10, 100, 20)
- (100, 10, 20)
2. Which of the following algorithm decreases the weight for commonly used words and increases the weights for words that are not used very much in a collection of documents?
- Term Frequency (TF)
- Inverse Document Frequency (IDF)
- Bag of words (BOW)
- None of the above
3. Which module in Python supports regular expressions?
- re
- regx
- pyregx
- None of the above
Advantages and Disadvantages of LSA
Latent Semantic Analysis can be very useful, but it does have its limitations. It’s important to understand both sides of LSA so you have an idea of when to leverage it and when to try something else.
Advantages of LSA
1. It is efficient and easy to implement.
2. It also gives decent results that are much better compared to the plain vector space model.
3. It is faster compared to other available topic modeling algorithms, as it involves document term matrix decomposition only.
Disadvantages of LSA
1. Since it is a linear model, it might not do well on datasets with non-linear dependencies.
2. LSA assumes a Gaussian distribution of the terms in the documents, which may not be true for all problems.
3. LSA involves SVD, which is computationally intensive and hard to update as new data comes up.
4. Lack of interpretable embeddings (we don’t know what the topics are, and the components may be arbitrarily positive/negative)
5. Need for a really large set of documents and vocabulary to get accurate results
6. It provides less efficient representation
Determining Optimal Number of Topics
Identifying the optimum number of topics in the given corpus text is not that easy task, sometimes this becomes a very challenging task. But, according to the problem statement, we can try the following options for determining the optimum number of topics:
1. The first method is to consider each topic as a separate cluster and find out the effectiveness of a cluster with the help of the Silhouette coefficient.
2. Topic coherence measure is a realistic measure for identifying the number of topics.
To evaluate topic models, Topic Coherence is a widely used metric. It uses the latent variable models. Each generated topic has a list of words. In topic coherence, we will find either the average or the median of pairwise word similarity scores of the words present in a topic.
Conclusion: The model will be considered as a good topic model if we got the high value of the topic coherence score.
Applications of LSA
The LSA is considered the pioneer for Latent Semantic Indexing (LSI) and Dimensionality Reduction algorithms.
1. The LSA can be used for dimensionality reduction. We can reduce the vector size drastically from millions to thousands without losing any context or information. As a result, it reduces the computation power and the time taken to perform the computation.
2. The LSA can be used in search engines. Latent Semantic Indexing(LSI) is the algorithm developed based on LSA, as the documents matching the given search query are found with the help of the vector that is developed from LSA.
3. LSA can also be used for document clustering. As we can see that the LSA assigns topics to each document based on the assigned topic so we can cluster the documents.
Self Learning: Read the following if you want to see a solved example of LSA:
Read for Solved Example
This ends our Part-16 of the Blog Series on Natural Language Processing!
Other Blog Posts by Me
You can also check my previous blog posts.
Previous Data Science Blog posts.
Here is my Linkedin profile in case you want to connect with me. I’ll be happy to be connected with you.
For any queries, you can mail me on Gmail.
End Notes
Thanks for reading!
I hope that you have enjoyed the article. If you like it, share it with your friends also. Something not mentioned or want to share your thoughts? Feel free to comment below And I’ll get back to you. 😉








