Support Vector Machine with Kernels and Python Iterators
This article was published as a part of the Data Science Blogathon.
Introduction
This article will cover the concepts of Iterators, Generators, and Decorators in Python. Later, we will discuss the Maximal-Margin Classifier and Soft Margin Classifier for Support Vector Machine. At last, we will learn about some SVM Kernels, such as Linear, Polynomial, and RBF. A data scientist often uses these advanced Python methods and SVM algorithms in his daily work. Understanding these concepts is rather confusing than it is difficult. As a Python newbie, anyone can get confused with Iterator, generator, and Decorators. To clear the confusion and better understand, we will discuss these concepts with their implementation in Python.
- Iterators
- Generator
- Decorator
- SVM
Iterators
Iterators are Objects or collections through which one can iterate element-wise. Examples of such iterators are List, Tuples, Sets, and Dictionaries.
Python has the ‘iter()’ keyword to create an Iterator and the ‘next()’ keyword to access the elements.
Now the question arises, “why do we create an iterator when we can iterate into a list, set, or dictionary directly?”
Iterators enable programmers to perform lazy operations. We can access the next element without traversing through previous elements. Hence, We need iterators to save CPU time and memory.
In-built iterator classes in Python, enumerate, reversed, zip, map, and filter.

Generators
Generators are expressions of function that create an iterator. A function returns a value while a generator returns an iterator. To create a generator ‘yield’ keyword is used instead of ‘return.’
We can use a generator object like an iterator, using the ‘next’ keyword or iterating through it using the ‘for’ loop.
Let’s see its implementation in Python:

The ‘yield’ keyword pauses the function in its defined state while the ‘return’ statement terminates that function.
A generator expression is different from a generator function. Such expressions get used as function arguments and created like list comprehensions.
Generator expressions use lazy evaluation and create one element once, while list comprehension computes an entire list.
Thus, generator expressions are much more memory efficient.
Decorators
As the name suggests, Decorators in Python function like objects used to decorate a function. The decorator takes a function as an argument and then applies its defined functionality to that function and returns the decorated function as its output.
Decorators get used for controlling or modifying the behaviour of function or class. We call a decorator before defining the function/class. There are two different kinds of decorators in Python:
- Class Decorators
- Function Decorators
Let’s implement the function decorator in Python

We can also define multiple decorators:

Support Vector Machine (SVM)
SVM is one of the most popular Machine Learning algorithms. This supervised algorithm gets used for both, Classification and Regression problems. Here, we will discuss the high-level concepts behind the SVM algorithm.
Maximal-Margin Classifier
This classifier is more of a hypothetical type that best explains the working of the SVM classifier.
This classifier creates a hyperplane and then classifies the inputs to either side of that hyperplane. A line that splits the input feature space is the hyperplane. The more the margin between the hyperplane and the prediction, the better it performs.

Let’s assume a dataset(x) with two input variables that form a two-dimensional space. And the target variable has binary labels, 0 and 1. Now, we can visualize the hyperplane as a line in this two-dimensional space. Let’s assume that the hyperplane separates all input points. For example:
B0+(W1*X1)+(W2*X2) = 0
W1 and W2 determine the line slope, and B0 is the intercept. X1 and X2 are two input feature vectors.
This line assists with classifying the input values using the equation.
- If the output of the equation is more than zero, the input lies above the line.
- If the equation returns a value less than zero, the point will lie below the line.
- An output value close to zero indicates that the input is close to the hyperplane. That point is difficult to classify.
- A large magnitude value may have more probability of correct classification.
The margin is the perpendicular distance between the line and the closest data point. The best line gets decided using an optimization procedure the optimal weights and bias. The best line that separates the two classes with the maximum margin is the Maximal-margin hyperplane.
Points that help in constructing the classifier and are relevant in determining the hyperplane are support vectors.
Soft Margin Classifier
The data we use in real life is often messy and can not be separated by a hyperplane. Therefore, the criteria for finding a hyperplane were relaxed, and a soft margin classifier was introduced. This softness enables the data points to violate the hyperplane line.
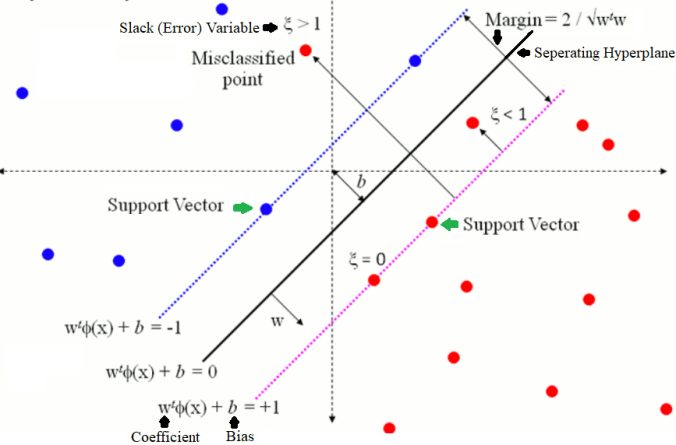
The soft margin classifier has additional parameters to provide the margin softness room in each dimension. This addition has increased the model complexity since it has more parameters for the model to fit the data to match such complexity.
One of such parameters is C which determines the allowed softness magnitude across all dimensions. This coefficient determines the flexibility range of margin violation. If the value of C=0, the flexibility is also none, and it is the same as Maximal-Margin. It indicates that the violations of hyperplane margin are directly proportional to C.
The training data points or examples that lie under the margin during the learning process of hyperplane are support vectors. These vectors also affect the position of the hyperplane, and C affects these points as well.
- The small value of C makes the algorithm more sensitive to the training data, leading to overfitting (High Variance and Low Bias).
- The large C reduces the sensitivity of the algorithm to the training data, leading to underfitting (Low Variance and High Bias).
Thus, the SVM algorithm determines the hyperplane to separate the classes. SVM uses Kernels to increase the complexity of the model to fit the more complex data.
Support Vector Machine Kernels
A kernel is nothing but the dot product. There are several kernels in SVM. Mostly, we use Linear, RBF, and Polynomial Kernels.
Linear Kernel
For binary classification, we use linear kernel or linear svm.
K(x, xi) = sum(x*xi)
For more complex classes or multi-class classification, we use more complex kernels.
Polynomial Kernel
The polynomial kernel uses polynomial expression instead dot product.
K(x, xi) = 1+ sum(x*xi)^d
d is the polynomial degree, a hyperparameter, and if d =1, it is the same as the linear svm.
Radial Basis Function (RBF)
It is a more complex kernel than the Polynomial and Gaussian Kernels.
K(x,xi) = exp(-gamma*sum(x*xi^2))
The hyperparameter gamma lies between 0 and 1, with the default value being 0.1. This local kernel can create complex segments inside the feature space.
Conclusion
In this article, we have learned some essential advanced Python concepts such as Iterators, Generators, and Decorators. Now let’s discuss some takeaways from this article:
- Iterators are Python objects that get used for creating more efficient collections of elements.
- Generators are Python functions that use the yield keyword and return an iterator.
- Generator expressions are more memory efficient since they insert one element once.
- Decorators are Python objects which get used for controlling or modifying function behaviour in Python.
- Support Vector Machine uses hyperplane to separate class instances using Maximal-margin and Soft Margin Classifier.
- Support Vector Machine kernels help with defining hyperplanes for more complex input space and multi-class classification.
Thank you for reading this article. For any feedback and query, feel free to reach me on Linkedin.
The media shown in this article is not owned by Analytics Vidhya and is used at the Author’s discretion.








