In my previous article, we talked about information retrieval and how machines can read the context from free text. Let’s talk about the biggest web information retrieval engine, Google, and the algorithm that powers its search results: the Google PageRank algorithm. Imagine you were to create a Google search in a world devoid of any search engine. What basic rules would you code to build such a search engine? If your answer is to use a Term Frequency or TF-IDF framework, consider the following case:
A user enters the query : “Harvard Business School“. He expects the first link to be “http://www.harvard.edu/”. But what would your algorithm do? It would try to find out pages which has the word “Harvard” maximum number of times, as “Business” and “School” will come out to be common words. Now, there is a possibility that “Harvard” keyword might not be repeated multiple times on Harvard’s own website. However, websites like Business school consultants or articles on business school might have this keyword multiple times. This leads these websites to achieve a rank much higher than the actual business school website. Thanks to the Google PageRank algorithm, which takes into account not only the frequency of keywords but also the quality and quantity of links to a website.
But, do search engines like Google face this challenge today? Obviously not! This is because they take help of an algorithm known as PageRank. In this article, we will discuss the concept of PageRank. In the next article, we will take this algorithm a step forward by leveraging it to find the most important packages in R.
Table of contents
An artificial web world
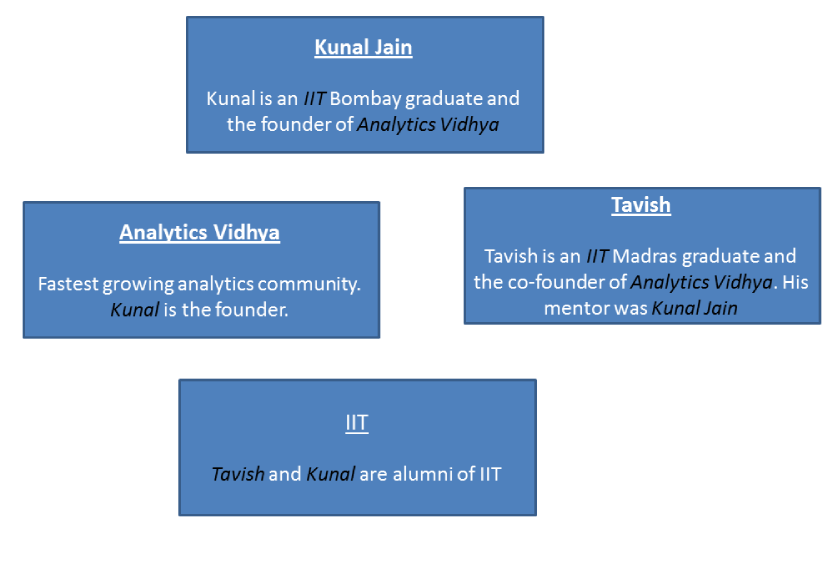
Imagine a web which has only 4 web pages, which are linked to each other. Each of the box below represents a web page. The words written in black and italics are the links between pages.
For instance, in the web page “Tavish”, it has 3 outgoing links : to the other three web pages. Now, let’s draw a simpler directed graph of this ecosystem.

Here is how Google ranks a page : The page with maximum number of incoming links is the most important page. In the current example, we see that the “Kunal Jain” page comes out as the most significant page.
Mathematical Formulation of Google Page Rank
First step of the formulation is to build a direction matrix. This matrix will have each cell as the proportion of the outflow. For instance, Tavish (TS) has 3 outgoing links which makes each proportion as 1/3.
Now we imagine that if there were a bot which will follow all the outgoing links, what will be the total time spent by this bot on each of these pages. This can be broken down mathematically into following equation :
A * X = X
Here A is the proportions matrix mentioned above
X is the probability of the bot being on each of these pages

Clearly, we see that Kunal Jain’s page in this universe comes out to be most important which goes in the same direction as our intuition.
Teleportation adjustments
Now, imagine a scenario where we have only 2 web pages : A and B. A has a link to B but B has no external links. In such cases, if you try solving the matrix, you will get a zero matrix. This looks unreasonable as B looks to be more important than A. But, our algorithm still gives same importance for both. To solve for this problem, a new concept of teleporatation was introduced. We include a constant probability of alpha to each of these pages. This is to compensate for instances where a user teleports from one webpage to other without any link. Hence, the equation is modified to the following equation :
(1-alpha) * A * X + alpha * b = X
Here, b is a constant unit column matrix. Alpha is the proportion of teleportation. The most common value taken for alpha is 0.15 (but can depend on different cases).
Other uses of PageRank Algorithm
Here are a few other uses of PageRank :
- Finding how well connected a person is on Social Media : One of the unexplored territory in social media analytics is the network information. Using this network information we can estimate how influential is the user. And therefore prioritize our efforts to please the most influential customers. Networks can be easily analyzed using Page Rank algorithm.
- Fraud Detection in Pharmaceutical industry : Many countries including US struggle with the problem of high percentage medical frauds. Such frauds can be spotted using Page Rank algorithm.
- Understand the importance of packages in any programming language : Page Rank algorithm can also be used to understand the layers of packages used in languages like R and Python. We will take up this topic in our next article.
Conclusion
In this article, we talked about PageRank mainly for search engines. But it’s not just for them! PageRank is used in many other areas like analyzing networks and suggesting things to people. It’s like a tool that has lots of jobs, not just one.
FAQs
PageRank is a Google algorithm that measures the importance of web pages based on the number and quality of links pointing to them. It assigns a numerical weighting to each page, with higher scores indicating greater importance. This weighting helps Google rank web pages in search results.
PageRank, a Google algorithm, measures web page importance based on link quantity and quality. Scores range from 0 to 10, with higher scores indicating greater importance. Aim for a PageRank of 5 or higher to improve search rankings and increase website traffic.
1. Create high-quality, relevant content.
2. Build backlinks from reputable websites.
3. Optimize your website for search engines (SEO).
4. Promote your website on social media and other channels.
5. Ensure technical SEO compliance.
6. Monitor and analyze your website’s performance.
7. Build an internal linking structure.
8. Earn user engagement and positive signals.
9. Remove low-quality backlinks.
10. Maintain patience and consistency.
Thinkpot: Can you think of more usage of Page Rank algorithm? Share with us useful links to leverage Page Rank algorithm in various fields.
Did you find this article useful? Do let us know your thoughts about this article in the box below.
If you like what you just read & want to continue your analytics learning, subscribe to our emails, follow us on twitter or like our facebook page.










This is very interesting. I am a beginner at R programming but I'd like to know how could you calculate X from the equation using R: A * X = X Same goes for teleportation adjustment equation: (1-alpha) * A * X + alpha * b = X How to calculate X given A, B & alpha ?
Chitranjan, A * X can be solved using a simultaneous equations. Lets say there are only 2 states with A = [[a1 , a2];[a3 , a4]] and X = [x1 , x2] A * X = [a1 x1 + a2 x2 , a3x1 + a4x2] Hence you need to solve, [a1 x1 + a2 x2 , a3x1 + a4x2] = [x1 , x2] =>a1 x1 + a2 x2 = x1 => a3x1 + a4x2 = x2 Here ai are all constants whereas xs are the changing variables. Similar kind of logic can be applied for the alpha equation. Hope this helps. Tavish
Tavish sir Thanks for helping the post. Sir In the above example which you mentioned I understand how you calculate A matrix using total probability is 1 and if has three outbound link so each may have probability 0.33. But I dont understand how do you arrive the figure of [0.40,0.12,0.24,0.24]. Could you please explain this. I am working in digital marketing company so want to know more about the algorithm Please show some link from where I can understand easily about the algorithm. I am waiting for your reply of both the questions.
Santu, This has been answered in my last comment. Let me know in case you still face an issue. Tavish
Other use of Page Ranking can be in Banking Industry for SKip Tracing in Collections. Page Rank can also be used in Credit Risk for Score Card preparation as one of the attaribute for Score card.
In Telecom Industry ,Page rank can be used to identify priority customer which is using most of the services of the operator with good amount of revenue.
Thanks Tavish! Insightful article. Quite some time back, I have done a course on edx "Networks, Crowds and Markets" from CornellX. Page Rank Algorithm was one of of the key components of the class and was demonstrated to be a key tool in analysing social networks with respect to markets. Before that I used to knew Page Rank as a Google's secret sauce only. I can relate a lot to that.
Tavish , Thanks for this wonderful article. I came across some of complex concepts explained in simple terms in your blog. Could you please publish an article on any practical example that uses Markov Chain Monte Carlo ?
Tavish, Thanks for this wonderful article. Other use of Page Ranking can be in Banking Industry for Skip Tracing in Collections. Page Rank can also be used in Credit Risk for Score Card preparation as one of the attributes for the Scorecard.
Tavish, Thanks for this wonderful article. The action or practice of locating people who are missing or have defaulted on a debt, especially as a profession.