Introduction
In the vast landscape of data exploration, where datasets sprawl like forests, hierarchical clustering acts as a guiding light, leading us through the dense thicket of information. Imagine a dendrogram, a visual representation of data relationships, branching out like a tree, revealing clusters and connections within the data. This is where machine learning meets the art of clustering, where Python serves as the wizard’s wand, casting spells of insight into the heart of datasets.
In this journey through the Python kingdom, we will unravel the mysteries of hierarchical clustering, exploring its intricacies and applications in data science. From dendrograms to distance matrices, from agglomerative to divisive clustering, we will delve deep into the techniques and methods that make hierarchical clustering a cornerstone of data analysis.
Join us as we embark on this adventure, where data points become nodes in a vast knowledge network, and clusters emerge like constellations in the night sky, guiding us toward the insights hidden within the data. Welcome to the world of hierarchical clustering in Python, where every cluster tells a story, and every dendrogram holds the key to unlocking the secrets of data science.
Study Material
- There are multiple ways to perform clustering. I encourage you to check out our awesome guide to the different types of clustering: An Introduction to Clustering and different methods of clustering
- To learn more about clustering and other machine learning algorithms (both supervised and unsupervised) check out the following comprehensive program- Certified AI & ML Blackbelt+ Program
Table of contents
- Introduction
- What is Hierarchical Clustering?
- Types of Hierarchical Clustering
- Supervised vs Unsupervised Learning
- Why Hierarchical Clustering?
- Steps to Perform Hierarchical Clustering
- How to Choose the Number of Clusters in Hierarchical Clustering?
- Solving the Wholesale Customer Segmentation Problem
- Conclusion
- Frequently Asked Questions?
Quiz Time
Welcome to the quiz on Hierarchical Clustering! Test your knowledge about this clustering technique and its key concepts.
What is Hierarchical Clustering?
Hierarchical clustering is an unsupervised learning technique for grouping similar objects into clusters. It creates a hierarchy of clusters by merging or splitting them based on similarity measures. It uses a bottom-up approach or top-down approach to construct a hierarchical data clustering schema.
Clustering Hierarchical groups similar objects into a dendrogram. It merges similar clusters iteratively, starting with each data point as a separate cluster. This creates a tree-like structure that shows the relationships between clusters and their hierarchy.
The dendrogram from hierarchical clustering reveals the hierarchy of clusters at different levels, highlighting natural groupings in the data. It provides a visual representation of the relationships between clusters, helping to identify patterns and outliers, making it a valuable tool for exploratory data analysis. For example, let’s say we have the below points, and we want to cluster them into groups:
We can assign each of these points to a separate cluster:
Now, based on the similarity of these clusters, we can combine the most similar clusters together and repeat this process until only a single cluster is left:
We are essentially building a hierarchy of clusters. That’s why this algorithm is called hierarchical clustering. I will discuss how to decide the number of clusters later. For now, let’s look at the different types of hierarchical clustering.
Also Read: Python Interview Questions to Ace Your Next Job Interview in 2024
Types of Hierarchical Clustering
There are mainly two types of hierarchical clustering:
- Agglomerative hierarchical clustering
- Divisive Hierarchical clustering
Let’s understand each type in detail.
Agglomerative Clustering Hierarchical
We assign each point to an individual cluster in this technique. Suppose there are 4 data points. We will assign each of these points to a cluster and hence will have 4 clusters in the beginning:
Then, at each iteration, we merge the closest pair of clusters and repeat this step until only a single cluster is left:
We are merging (or adding) the clusters at each step, right? Hence, this type of clustering is also known as additive hierarchical clustering.
Divisive Hierarchical Clustering
Divisive Clustering Hierarchical works in the opposite way. Instead of starting with n clusters (in case of n observations), we start with a single cluster and assign all the points to that cluster.
So, it doesn’t matter if we have 10 or 1000 data points. All these points will belong to the same cluster at the beginning:
Now, at each iteration, we split the farthest point in the cluster and repeat this process until each cluster only contains a single point:

We are splitting (or dividing) the clusters at each step, hence the name divisive hierarchical clustering.
Agglomerative Clustering is widely used in the industry and will be the article’s focus. Divisive hierarchical clustering will be a piece of cake once we have a handle on the agglomerative type
Also Read: Python Tutorial to Learn Data Science from Scratch
Applications of Hierarchical Clustering
Here are some common applications of hierarchical clustering:
- Biological Taxonomy: Hierarchical clustering is extensively used in biology to classify organisms into hierarchical taxonomies based on similarities in genetic or phenotypic characteristics. It helps understand evolutionary relationships and biodiversity.
- Document Clustering: In natural language processing, hierarchical clustering groups similar documents or texts. It aids in topic modeling, document organization, and information retrieval systems.
- Image Segmentation: Hierarchical clustering segments images by grouping similar pixels or regions based on color, texture, or other visual features. It finds applications in medical imaging, remote sensing, and computer vision.
- Customer Segmentation: Businesses use hierarchical clustering to group customers into groups based on their purchasing behaviors, demographics, or preferences. This helps with targeted marketing, personalized recommendations, and customer relationship management.
- Anomaly Detection: Hierarchical clustering can identify outliers or anomalies in datasets by isolating data points that do not fit well into any cluster. It is useful in fraud detection, network security, and quality control.
- Social Network Analysis: Hierarchical clustering helps uncover community structures or hierarchical relationships in social networks by clustering users based on their interactions, interests, or affiliations. It aids in understanding network dynamics and identifying influential users.
- Market Basket Analysis: Retailers use hierarchical clustering to analyze transaction data and identify associations between products frequently purchased together. It enables them to optimize product placements, promotions, and cross-selling strategies.
Advantages and Disadvantages of Hierarchical Clustering
Here are some advantages and disadvantages of hierarchical clustering:
Advantages of hierarchical clustering:
- Easy to interpret: Hierarchical clustering produces a dendrogram, a tree-like structure that shows the order in which clusters are merged. This dendrogram provides a clear visualization of the relationships between clusters, making it easy to interpret the results.
- No need to specify the number of clusters: Unlike other clustering algorithms, such as k-means, hierarchical clustering does not require you to specify the number of clusters beforehand. The algorithm determines the number of clusters based on the data and the chosen linkage method.
- Captures nested clusters: Hierarchical clustering captures the hierarchical structure in the data, meaning it can identify clusters within clusters (nested clusters). This can be useful when the data naturally forms a hierarchy.
- Robust to noise: Hierarchical clustering is robust to noise and outliers because it considers the entire dataset when forming clusters. Outliers may not significantly affect the clustering process, especially if a suitable distance metric and linkage method are chosen.
Disadvantages of hierarchical clustering:
- Computational complexity: Hierarchical clustering can be computationally expensive, especially for large datasets. The time complexity of hierarchical clustering algorithms is typically 𝑂(𝑛2log𝑛)O(n2logn) or 𝑂(𝑛3)O(n3), where 𝑛n is the number of data points.
- Memory usage: Besides computational complexity, hierarchical clustering algorithms can consume a lot of memory, particularly when dealing with large datasets. Storing the entire distance matrix between data points can require substantial memory.
- Difficulty with large datasets: Due to its computational complexity and memory requirements, hierarchical clustering may not be suitable for large datasets. In such cases, alternative clustering methods, such as k-means or DBSCAN, may be more appropriate.
- Sensitive to noise and outliers: While hierarchical clustering is generally robust to noise and outliers, extreme outliers or noise points can still affect the clustering results, especially if they are not handled properly beforehand.
- Difficulty in merging clusters: Once clusters are formed in hierarchical clustering, merging or splitting them can be difficult, especially if the clustering uses a divisive method. This lack of flexibility can be a limitation in certain scenarios where cluster adjustments are needed.
Application of Hierarchical Clustering with Python
In Python, the scipy and scikit-learn libraries are often used to perform hierarchical clustering. Here’s how you can apply hierarchical clustering using Python:
- Import Necessary Libraries: First, you’ll need to import the necessary libraries:
numpyfor numerical operations,matplotlibfor plotting, andscipy.cluster.hierarchyfor hierarchical clustering. - Generate or Load Data: You can either generate a synthetic dataset or load your dataset.
- Compute the Distance Matrix: Compute the distance matrix which will be used to form clusters.
- Perform Hierarchical Clustering: Use the linkage method to perform hierarchical clustering.
- Plot the Dendrogram: Visualize the clusters using a dendrogram.
Here’s an example of hierarchical clustering using Python:
import numpy as np
import matplotlib.pyplot as plt
from scipy.cluster.hierarchy import dendrogram, linkage
from scipy.cluster.hierarchy import fcluster
from sklearn.datasets import make_blobs
# Generate sample data
X, y = make_blobs(n_samples=100, centers=3, cluster_std=0.60, random_state=0)
# Compute the linkage matrix
Z = linkage(X, 'ward')
# Plot the dendrogram
plt.figure(figsize=(10, 7))
plt.title("Dendrogram")
plt.xlabel("Sample index")
plt.ylabel("Distance")
dendrogram(Z)
plt.show()
# Determine the clusters
max_d = 7.0 # this can be adjusted based on the dendrogram
clusters = fcluster(Z, max_d, criterion='distance')
# Plot the clusters
plt.figure(figsize=(10, 7))
plt.scatter(X[:, 0], X[:, 1], c=clusters, cmap='prism')
plt.title("Hierarchical Clustering")
plt.xlabel("Feature 1")
plt.ylabel("Feature 2")
plt.show()
Supervised vs Unsupervised Learning
Understanding the difference between supervised and unsupervised learning is important before we dive into the Clustering hierarchy. Let me explain this difference using a simple example.
Suppose we want to estimate the count of bikes that will be rented in a city every day:

Or, let’s say we want to predict whether a person on board the Titanic survived or not:

Examples
- In the first example, we have to predict the number of bikes based on features like the season, holiday, working day, weather, temperature, etc.
- In the second example, we are predicting whether a passenger survived. In th’ ‘Surviv’d’ variable, 0 represents that the person did not survive, and 1 means the person did make it out alive. The independent variables here include Pclass, Sex, Age, Fare, etc.
Let’s look at the figure below to understand this visually:
Here, y is our dependent or target variable, and X represents the independent variables. The target variable is dependent on X, also called a dependent variable. We train our model using the independent variables to supervise the target variable. Hence, the name supervised learning.
When training the model, we aim to generate a function that maps the independent variables to the desired target. Once the model is trained, we can pass new sets of observations, and the model will predict their target. This, in a nutshell, is supervised learning.
In these cases, we try to divide the entire data into a set of groups. These groups are known as clusters, and the process of making them is known as clustering.
This technique is generally used for clustering a population into different groups. A few common examples include segmenting customers, clustering similar documents, recommending similar songs or movies, etc.
There are many more applications of unsupervised learning. If you come across any interesting ones, feel free to share them in the comments section below!
Various algorithms help us make these clusters. The most commonly used clustering algorithms are K-means and Hierarchical clustering
Why Hierarchical Clustering?
We should first know how K-means works before we dive into hierarchical clustering. Trust me, it will make the concept of hierarchical clustering much easier.
Here’s a brief overview of how K-means works:
- Decide the number of clusters (k)
- Select k random points from the data as centroids
- Assign all the points to the nearest cluster centroid
- Calculate the centroid of newly formed clusters
- Repeat steps 3 and 4
It is an iterative process. It will keep on running until the centroids of newly formed clusters do not change or the maximum number of iterations are reached.
But there are certain challenges with K-means. It always tries to make clusters of the same size. Also, we have to decide the number of clusters at the beginning of the algorithm. Ideally, we would not know how many clusters should we have, in the beginning of the algorithm and hence it a challenge with K-means.
This is a gap hierarchical clustering bridge with aplomb. It takes away the problem of having to pre-define the number of clusters. Sounds like a dream! So, let’s see what hierarchical clustering is and how it improves on K-means.
How Does Hierarchical Clustering Improve on K-means?
Hierarchical clustering and K-means are popular clustering algorithms but have different strengths and weaknesses. Here are some ways in which hierarchical clustering can improve on K-means:
1. No Need to Pre-specify Number of Clusters
Hierarchical Clustering:
- Does not require the number of clusters (k) to be specified in advance.
- The dendrogram provides a visual representation of the hierarchy of clusters, and the number of clusters can be determined by cutting the dendrogram at a desired level.
K-means:
- Requires the number of clusters (k) to be specified beforehand, which can be difficult if the optimal number of clusters is unknown.
2. Captures Nested Clusters
Hierarchical Clustering:
- It can identify nested clusters, meaning it can find clusters within them.
- This is useful for datasets with a natural hierarchical structure (e.g., taxonomy of biological species).
K-means:
- Assumes clusters are flat and do not capture hierarchical relationships.
3. Flexibility with Cluster Shapes
Hierarchical Clustering:
- Can find clusters of arbitrary shapes.
- The algorithm is not restricted to spherical clusters and can capture more complex cluster structures.
K-means:
- Assumes clusters are spherical and of similar size, which may not be suitable for datasets with irregularly shaped clusters.
4. Distance Metrics and Linkage Criteria
Hierarchical Clustering:
- Offers flexibility in distance metrics (e.g., Euclidean, Manhattan) and linkage criteria (e.g., single, complete, average).
- This flexibility can improve clustering performance on different types of data.
K-means:
- Typically, it uses the Euclidean distance, which may not be suitable for all data types.
5. Handling Outliers
Hierarchical Clustering:
- Outliers can be identified as singleton clusters at the bottom of the dendrogram.
- This makes it easier to detect and potentially remove outliers.
K-means:
- Sensitive to outliers, as they can significantly affect the position of cluster centroids.
6. Robustness to Initialization
Hierarchical Clustering:
- Does not require random initialization of cluster centroids.
- The clustering result is deterministic and does not depend on initial conditions.
K-means:
- Requires random initialization of centroids, leading to different clustering results in different runs.
- The algorithm may converge to local minima, depending on the initial placement of centroids.
7. Visual Interpretation
Hierarchical Clustering:
- The dendrogram provides a visual and interpretable representation of the clustering process.
- It helps in understanding the relationships between clusters and the data structure.
K-means:
- Provides cluster labels and centroids, but does not visually represent the clustering process.
Practical Example
Let’s consider a practical example using hierarchical clustering and K-means on a simple dataset:
import numpy as np
import matplotlib.pyplot as plt
from scipy.cluster.hierarchy import dendrogram, linkage
from sklearn.datasets import make_blobs
from sklearn.cluster import KMeans
# Generate sample data
X, y = make_blobs(n_samples=100, centers=3, cluster_std=0.60, random_state=0)
# Hierarchical Clustering
Z = linkage(X, 'ward')
plt.figure(figsize=(10, 7))
plt.title("Hierarchical Clustering Dendrogram")
dendrogram(Z)
plt.show()
# K-means Clustering
kmeans = KMeans(n_clusters=3, random_state=0).fit(X)
labels = kmeans.labels_
plt.figure(figsize=(10, 7))
plt.scatter(X[:, 0], X[:, 1], c=labels, cmap='prism')
plt.title("K-means Clustering")
plt.show()
Steps to Perform Hierarchical Clustering
We merge the most similar points or clusters in hierarchical clustering – we know this. Now the question is – how do we decide which points are similar and which are not? It’s one of the most important questions in clustering!
Here’s one way to calculate similarity – Take the distance between the centroids of these clusters. The points having the least distance are referred to as similar points and we can merge them. We can refer to this as a distance-based algorithm as well (since we are calculating the distances between the clusters).
In hierarchical clustering, we have a concept called a proximity matrix. This stores the distances between each point. Let’s take an example to understand this matrix and the steps to perform hierarchical clustering.
Setting up the Example
Suppose a teacher wants to divide her students into different groups. She has the marks scored by each student in an assignment and based on these marks, she wants to segment them into groups. There’s no fixed target here as to how many groups to have. Since the teacher does not know what type of students should be assigned to which group, it cannot be solved as a supervised learning problem. So, we will try to apply hierarchical clustering here and segment the students into different groups.
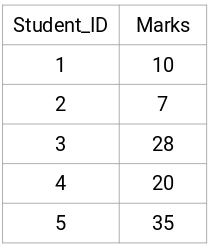
Let’s take a sample of 5 students:
Creating a Proximity Matrix
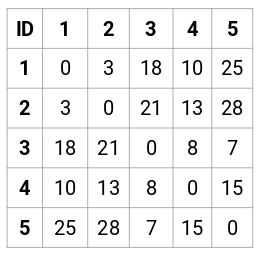
First, we will create a proximity matrix which will tell us the distance between each of these points. Since we are calculating the distance of each point from each of the other points, we will get a square matrix of shape n X n (where n is the number of observations).
Let’s make the 5 x 5 proximity matrix for our example:
The diagonal elements of this matrix will always be 0 as the distance of a point with itself is always 0. We will use the Euclidean distance formula to calculate the rest of the distances. So, let’s say we want to calculate the distance between point 1 and 2:
√(10-7)^2 = √9 = 3
Similarly, we can calculate all the distances and fill the proximity matrix.
Steps to Perform Hierarchical Clustering
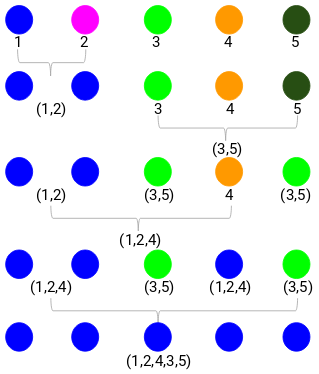
Step 1: First, we assign all the points to an individual cluster:
Different colors here represent different clusters. You can see that we have 5 different clusters for the 5 points in our data.
Step 2: Next, we will look at the smallest distance in the proximity matrix and merge the points with the smallest distance. We then update the proximity matrix:
Here, the smallest distance is 3 and hence we will merge point 1 and 2:

Let’s look at the updated clusters and accordingly update the proximity matrix:
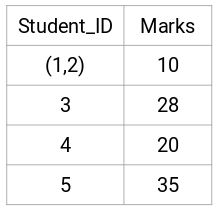
Here, we have taken the maximum of the two marks (7, 10) to replace the marks for this cluster. Instead of the maximum, we can also take the minimum value or the average values as well. Now, we will again calculate the proximity matrix for these clusters:
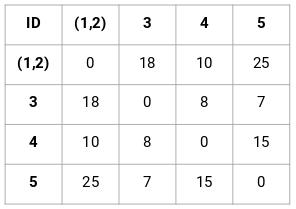
Step 3: We will repeat step 2 until only a single cluster is left.
So, we will first look at the minimum distance in the proximity matrix and then merge the closest pair of clusters. We will get the merged clusters as shown below after repeating these steps:
We started with 5 clusters and finally had a single cluster. This is how agglomerative hierarchical clustering works. But the burning question remains—how do we decide the number of clusters? Let’s understand that in the next section.
How to Choose the Number of Clusters in Hierarchical Clustering?
Are you ready to finally answer this question that’s been hanging around since we started learning? To get the number of clusters for hierarchical clustering, we use an awesome concept called a Dendrogram.
A dendrogram is a tree-like diagram that records the sequences of merges or splits.
Example
Let’s get back to the teacher-student example. Whenever we merge two clusters, a dendrogram will record the distance between them and represent it in graph form. Let’s see how a dendrogram looks:
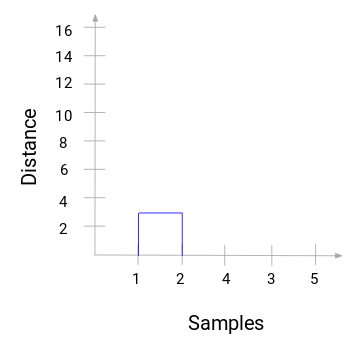
We have the samples of the dataset on the x-axis and the distance on the y-axis. Whenever two clusters are merged, we will join them in this dendrogram, and the height of the join will be the distance between these points. Let’s build the dendrogram for our example:
Take a moment to process the above image. We started by merging sample 1 and 2 and the distance between these two samples was 3 (refer to the first proximity matrix in the previous section). Let’s plot this in the dendrogram:
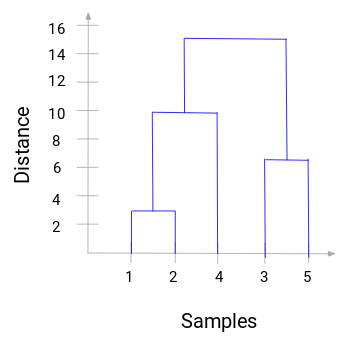
Here, we can see that we have merged samples 1 and 2. The vertical line represents the distance between these samples. Similarly, we plot all the steps where we merged the clusters, and finally, we get a dendrogram like this:
We can visualize the steps of hierarchical clustering. The more the distance of the vertical lines in the dendrogram, the more the distance between those clusters.
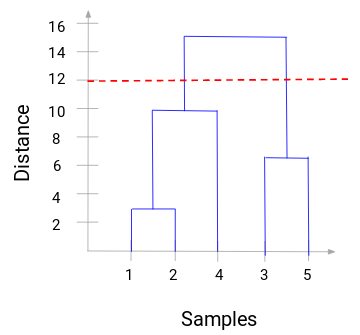
Now, we can set a threshold distance and draw a horizontal line (Generally, we try to set the threshold so that it cuts the tallest vertical line). Let’s set this threshold as 12 and draw a horizontal line:
The number of clusters will be the number of vertical lines intersected by the line drawn using the threshold. In the above example, since the red line intersects 2 vertical lines, we will have 2 clusters. One cluster will have a sample (1,2,4) and the other will have a sample (3,5).
Solving the Wholesale Customer Segmentation Problem
Time to get our hands dirty in Python!
We will be working on a wholesale customer segmentation problem. You can download the dataset using this link. The data is hosted on the UCI Machine Learning repository. This problem aims to segment the clients of a wholesale distributor based on their annual spending on diverse product categories, like milk, grocery, region, etc.
Let’s explore the data first and then apply Hierarchical Clustering to segment the clients.
Required Libraries
Load the data and look at the first few rows:
Python Code
There are multiple product categories – Fresh, Milk, Grocery, etc. The values represent the number of units each client purchases for each product. We aim to make clusters from this data to segment similar clients. We will, of course, use Hierarchical Clustering for this problem.
But before applying, we have to normalize the data so that the scale of each variable is the same. Why is this important? If the scale of the variables is not the same, the model might become biased towards the variables with a higher magnitude, such as fresh or milk (refer to the above table).
So, let’s first normalize the data and bring all the variables to the same scale:
Here, we can see that the scale of all the variables is almost similar. Now, we are good to go. Let’s first draw the dendrogram to help us decide the number of clusters for this particular problem:

The x-axis contains the samples and y-axis represents the distance between these samples. The vertical line with maximum distance is the blue line and hence we can decide a threshold of 6 and cut the dendrogram:
We have two clusters as this line cuts the dendrogram at two points. Let’s now apply hierarchical clustering for 2 clusters:
We can see the values of 0s and 1s in the output since we defined 2 clusters. 0 represents the points that belong to the first cluster and 1 represents points in the second cluster. Let’s now visualize the two clusters:
Awesome! We can visualize the two clusters here. This is how we can implement hierarchical clustering in Python.
Conclusion
In our journey, we’ve uncovered a powerful tool for unraveling the complexities of data relationships. From the conceptual elegance of dendrograms to their practical applications in diverse fields like biology, document analysis, cluster analysis, and customer segmentation, hierarchical cluster analysis emerges as a guiding light in the labyrinth of data exploration.
As we conclude this expedition, we stand at the threshold of possibility, where every cluster tells a story, and every dendrogram holds the key to unlocking the secrets of data science. In the ever-expanding landscape of Python and machine learning, hierarchical clustering stands as a stalwart companion, guiding us toward new horizons of discovery and understanding.
If you are still relatively new to data science, I highly recommend taking the Applied Machine Learning course. It is one of the most comprehensive end-to-end machine learning courses you will find anywhere. Hierarchical clustering is just one of the diverse topics we cover in the course.
What are your thoughts on hierarchical clustering? Do you feel there’s a better way to create clusters using less computational resources? Connect with me in the comments section below, and let’s discuss!
Frequently Asked Questions?
A. Hierarchical K clustering is a method of partitioning data into K clusters where each cluster contains similar data points organized in a hierarchical structure.
A. An example of a hierarchical cluster could be grouping customers based on their purchasing behavior, where clusters are formed based on similarities in purchasing patterns, leading to a hierarchical tree-like structure.
A. The two methods of hierarchical clustering are:
1. Agglomerative hierarchical clustering: It starts with each data point as a separate cluster and merges the closest clusters together until only one cluster remains.
2. Divisive hierarchical clustering: It begins with all data points in one cluster and recursively splits the clusters into smaller ones until each data point is in its cluster.
A. Hierarchical clustering of features involves clustering features or variables instead of data points. It identifies groups of similar features based on their characteristics, enabling dimensionality reduction or revealing underlying patterns in the data.























Dear Pulakit Sharma, Thank you very much for your article. Is it possible to use R to get the same output. Your reply will be much appreciated.
Hi Thanks for sharing very informative and useful. I have one question once we cluster the data how do find the factor or variable which differentiate the cluster. For eg if age is a factor then all the cluster should have the different age bins this way we can say that age is a factor which differentiate the clusters. My question how do we find when we have n variables ? Thanks
Really well explained for beginners. As already mentioned in article clustering is very challenging for data analyst and always requires plenty of expertise
Hi Pulkit, I really applaud your efforts to effectively communicate the concepts of Machine Learning with visualisations. I am not a ML practitioner but I am a student and I have recently studied these subjects recently. I would like to add few points to the above article. Firstly, I think the scaling operation that you have performed has been done on the categorical variables. I dont think categorical variables need to undergo the scaling and transformation(normalisation). The above normalised data for region and channel do not make any sense. Secondly, the drawbacks of hierarchical clustering have not been posted here. The drawbacks of Hierarchical clustering is that they do not perform well with large datasets. I hope my inputs are helpful to you. Regards, MD
Thank you for your inputs! They will surely be helpful for the community.
Hi, I feel that the categorical variables should be converted to dummy variables first and then scaling should be applied. One cannot use both categorical and numeric variables together in this type of clustering. k-proto should be used in that case. The following code should be used and then data should be scaled: data_new=pd.get_dummies(data, columns=['Channel', 'Region'],drop_first=True) Thanks
Amazing post, thanks for sharing.
Glad you liked it!
can you please share the python code to do this clustering . what u have said is theoretical . How to do it in python notebook ???
Hi Saurabh, At the end of the article, I have included the codes as well for hierarchical clustering.
Please explain how to perform clustering if the number of variables are more than 20.
Hi, The process will be same even if the number of variables are more. If the number of variables is very large, you can first perform some dimensionality reduction techniques to reduce the variables and then perform clustering on the reduced dimension. To learn how to reduce the dimensions, you can refer this blog: https://www.analyticsvidhya.com/blog/2018/08/dimensionality-reduction-techniques-python/
Awesome! We can clearly visualize the two clusters here, in reality, we have to get the nest cluster out so that we can target this group. None of the articles or training shows that. All end up with visualizations.
Hi, thanks for this article, I still can't find the code. Can you please share that link for the code here.
Hi Mary, The codes are provided in the "Solving the Wholesale Customer Segmentation problem using Hierarchical Clustering" section of the article.
How to do this for categorical variables?
Hi Ankur, You can first convert the categorical variable into numbers using either one hot encoding, or label encoding and then apply this clustering technique on the converted data.
Hi! I find it really interesting, I'll try to apply it with documents to cluster them.
Glad you found it helpful!
Hi, great job. I only have binary values for my variables, what can I do?
Hi Mauro, You can use this technique.
Dear Pulkit, Thank you very much for making this easy-to-follow demo! My question is - how do I append the calculated cluster labels to my original 'data' DataFrame? So I know which row (customer) belongs to each cluster. Thank you
Hi Michael, You can first store the predictions in a variable, let's say 'prediction' as: prediction = cluster.fit_predict(data_scaled) Now, you can create a new column in your dataframe and store these predictions in it as: data['predictions'] = prediction This will save the predictions into your dataframe.
Lets say I want to cut at 2.7, so I have 7 clusters. How will the clusters be numbered? Does that mean that (2,3) will be "closer" and (4,5) also will be closer, also (6,7) and (1) will be closer to (2,3)? How can I make sure that the numbering correctly corresponds to the hierarchy shown in the dendrogram? Thanks! Michael
Hi Michael, If you cut at 2.7, you will get 7 different clusters and they would look like this. I am not sure what do you mean by (2,3), (4,5), (6,7) and (1) here. Please elaborate it more.
Another question: Since the dendrogram linkage already shows the connections between the data - it must be calculating the Euclidean distances... So it is ACTUALLY doing the clustering already, not just the visualization... So why should I run AgglomerativeClustering at all? Can't I simply somehow output the connections that the dendrogram found - as data, not visual? And why AgglomerativeClustering result has to be consistent with dendrogram's? Is it the SAME algorithm? It feels to me that we are using two clusterings here... Thanks!
Hi Michael, Both Dendrogram and agglomirative clustering produces the same results. Dendrogram is a way to visualize the clusters and then decide the suitable number of clusters. I idea behind both these is same. We combine the two closest points or clusters. Dendrogram is basically used to determine the number of clusters that you should have.
I am working on school project, vessel prediction from AIS data. the data corresponds to an observation of a single maritime vessel at a single point in time(more like a position report). We have to track the movements of the different vessels given these reports over time. Do you think Hierarchical clustering is the best choice for this problem? How can we find the minimum distance between each cluster? In your example you decided to take the maximum distance which was the blue line in the dendrogram. I followed your steps on the data I have and I feel like I need a way to figure out the min distance between the clusters not the max; cause I will always get 2 clusters which is not ideal here!! Thanks!
Hi Elissa, Can you share the screenshot of the dendrogram that you got? That would help me to guide you in a better way.
hi Pulkit, how you choose the x and y variable for plt.scatter?in your example you choose 'milk' as x and 'grocery' as y. in my case i have many variable. when i choose different x and y its give me different graph..and looks like the clustering not clear see as a group. thanks hazlan
Hi Hazlan, In real life scenarios, the number of variables will be more. And as the number of variables increases, visualization becomes more and more difficult. So, it is very tough to visualize the clusters in high dimension. You can pick the variables which you think are important as per your dataset and then visualize those variables.
Really good write-up!
Thank you Jonathan!
How dendograms caluculates distance/linkage between two samples(having more than 2 features like region, fresh, milk, grocery). How does it do ?
I found the article very useful but the calculation part of the distance matrix has been done correctly. The concept was clear and I found the distance matrix has two same values[(1,2), (5,3)] at the initial. I don't know why you avoided this basic math in the proximity matrix that too at the very beginning of the description.
I really enjoyed your write-up!. I have few questions. I'm working on a fortune500 dataset. 1) How do you know when a problem is a prediction problem or an Interpretation problem? 2) Why did we have to cut the dendrogram at the threshold of the blue line? Why can't we just use the whole number of cluster? I'm a novice! I will really appreciate your explanations.
I really enjoyed your write-up!. I have few questions. I'm working on a fortune500 dataset. 1) How do you know when a problem is a prediction problem or an Interpretation problem? 2) Why did we have to cut the dendrogram at the threshold of the blue line? Why can't we just use the whole number of cluster? I'm a novice! I will really appreciate your explanations.
Dear Pulakit Sharma, Thank you very much for your article.I have a technical question, how should I do hierarchical clustering if I use my own obtained distance matrix? Also, how do I locate the time series I use into the original data after clustering?
Very interesting. Thank you
hello sir how did you label the "milk" and "Grocery" in the last step .
When calculating distance, you are just calculating the square root of a square. Is this the correct method?