Introduction
Excel for predictive modeling? Really?
That’s typically the first reaction I get when I bring up the subject. This is followed by an incredulous look when I demonstrate how we can leverage the flexible nature of excel predictive analyticsto build predictive models for our data science and analytics projects.
Let me ask you a question – if the shops around you started collecting customer data, could they adopt a data-based strategy to sell their goods? Can they forecast their sales or estimate the number of products that might be sold?

Now you must be wondering how in the world will they build a complex statistical model that can predict these things? And learning analytics or hiring an analyst might be beyond their scope. Here’s the good news – they don’t need to. Microsoft Excel offers us the ability to conjure up predictive models without having to write complex code that flies over most people’s heads.
We can easily build a simple model like linear regression in attrition prediction model in excel that can help us perform analysis in a few simple steps. And we don’t need to be a master in Excel or Statistics to perform predictive modeling!
Overview
- You can perform predictive modeling in Excel in just a few steps
- Here’s a step-by-step tutorial on how to build a linear regression model in Excel and how to interpret the results
In this article, I am going to explain how to build a linear regression model in attrition prediction model in excel and how to analyze the result so that you can become a superstar analyst!
This is the seventh article in my Excel for Analysts series. I highly recommend going through the previous articles to become a more efficient analyst:
- 3 Advanced Excel Charts Every Analytics Professional Should Try
- 5 Powerful Excel Dashboards for Analytics Professionals
- 5 Useful Excel Tricks to Become an Efficient Analyst
- 5 Excel Tricks You’ll Love Working with as an Analyst
- 5 Handy Excel Tricks for Conditional Formatting Every Analyst Should Know
- 3 Classic Excel Tricks to Become an Efficient Analyst
I encourage you to check out the below resources if you’re a beginner in Excel and Business Analytics:
Table of contents
What is Linear Regression?
Linear Regression is the first machine learning technique most of us learn. It’s also the most commonly used supervised learning technique in the industry.
But what is linear regression?
It is a linear approach to statistically model the relationship between the dependent variable (the variable you want to predict) and the independent variables (the factors used for predicting). Linear regression gives us an equation like this:

Here, we have Y as our dependent variable, X’s are the independent variables and all C’s are the coefficients. Coefficients are basically the weights assigned to the features, based on their importance.
The most common method to perform regression is the OLS (Ordinary Least Squares). Its goal is to reduce the sum of squares to produce the line of best fit like this:
If you want to learn more about linear regression, here are some resources:
- Fundamentals of Linear Regression
- Diagnostic Plots in a Linear regression model
- A Beginner’s Guide to Linear Regression in Excel
Getting the All-Important Analysis ToolPack Excel Add-in
To perform a regression analysis in attrition prediction model in excel, we first need to enable Excel’s Analysis ToolPak Add-in. The Analysis ToolPak in excel predictive analytics is an add-in program that provides data analysis tools for statistical and engineering analysis.
To add it in your workbook, follow these steps.
Step 1 – Excel Options
Go to Files -> Options:

Step 2 – Locate Analytics ToolPak
Go to Add-ins on the left panel -> Manage Excel Add-ins -> Go:

Step 3 – Add Analytics ToolPak
Select the “Analysis ToolPak” and press OK:

You have successfully added the Analysis ToolPak in Excel! You can check it by going to the Data bar in the Ribbon.
Let’s start building our predictive model in Excel!
Implementing Linear Regression in Excel
A lot of the stuff was theoretical so far. Now, let’s deep-dive into excel predictive analytics and perform linear regression analysis!
Here is the problem statement we will be working with:
There is a shoe selling company in the town of Winden. The company wants to predict the sales through each customer by considering the following factors – Income of customer, Distance of home from store, customer’s running frequency per week.
Step 1 – Select Regression
Go to Data -> Data Analysis:

Go to Data Analysis in the Data ToolPak, select Regression and press OK:

Step 2 – Select Options
In this step, we will select some of the options necessary for our analysis, such as :
- Input y range – The range of independent factor
- Input x range – The range of dependent factors
- Output range – The range of cells where you want to display the results

The other options are discretionary and you may select them for your specific purpose.
Press OK and we have finally made a regression analysis in Excel in just two steps! Wasn’t that easy? Now we will see the result of regression analysis in excel.
Analyzing our Predictive Model’s Results in Excel
Implementing the linear regression model was the easy part. Now comes the tricky aspect of our analysis – interpreting the predictive model’s results in excel predictive analytics.
In the summary, we have 3 types of output and we will cover them one-by-one:
- Regression statistics table
- ANOVA table
- Regression coefficients table
- Residual Table
Regression Statistics Table
The regression statistics table tells us how well the line of best fit defines the linear relationship between the independent and dependent variables. Two of the most important measures are the R squared and Adjusted R squared values.
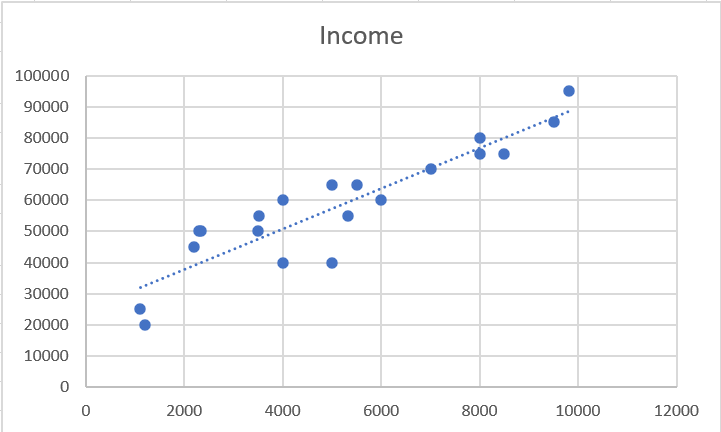
The R-squared statistic is the indicator of goodness of fit which tells us how much variance is explained by the line of best fit. R-squared value ranges from 0 to 1. In our case, we have the R-squared value of 0.953 which means that our line is able to explain 95% of the variance – a good sign.
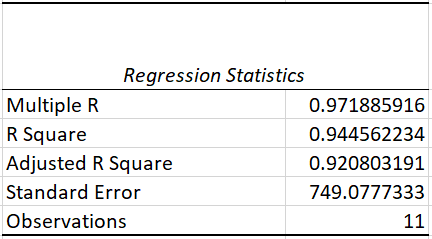
But there is a problem – as we keep adding more variables, our R squared value will keep increasing even though the variable might not be having any effect. Adjusted R-squared solves this problem and is a much more reliable metric.
ANOVA Table
ANOVA stands for Analysis of Variance. This table breaks down the sum of squares into its components to give details of variability within the model.
It includes a very important metric, Significance F (or the P-value) , which tells us whether your model is statistically significant or not. In a nutshell, it means that our results are likely not due to randomness but because of an underlying cause. The most used threshold for the p-value is 0.05. If we are getting a value less than this, than we are good to go. Otherwise, we would need to choose another set of independent variables.

In our case, we have a value well below the threshold of 0.05. Awesome, we can move forward now!
Regression Coefficient Table
The Coefficient table breaks down the components 0f the regression line in the form of coefficients. We can understand a lot from these.
For the Winden shoe company, it seems that for each unit increase in income, the sale increases by 0.08 units, and an increase in one unit of distance from store increases by 508 units!

It seems that an increase in running frequency decreases the sales by 24 units, but can we actually believe in this feature? If you look in the image above, you will notice that it’s p-value is greater than 0.5 which means it is not statistically significant. We will look into how we can handle this situation in the next section.
Residual Table
The residual table reflects how much the predicted value varies from the actual value. It consists of the values predicted by our model:

How can we Improve our Model?
As we saw previously, the p-value for the variable running frequency is more than 0.05 so let us check our results by removing this variable from our analysis.
We will follow all the steps mentioned above but we will not include the running frequency column:

We notice that the value of adjusted R-squared improved slightly here from 0.920 to 0.929!
Making Predictions in Excel!
We have the regression analysis ready so what can we do now? Let’s see.
An old customer of yours named Aleksander walks in and we wish to predict the sales from him. We can simply plug in the number from the data in the linear regression model and we are good to go!
Aleksander has an income of 40k and lives 2km away from the store. What is the estimated sales?
The equation becomes:

Here, our model has estimated that Mr. Aleksander would pay 4218 units to buy his new pair of shoes! That’s the power of linear regression done simply in Microsoft Excel.
Conclusion
Excel proves to be a powerful tool for predictive modeling, making data analysis accessible even to those without extensive coding knowledge. By following the steps outlined in this article, analysts can easily build and interpret linear regression models using Excel’s Analysis ToolPak. This approach enables businesses of all sizes to leverage their data for forecasting and decision-making. While more complex models may require specialized software, Excel’s linear regression capabilities offer a solid foundation for predictive analytics, empowering users to derive valuable insights from their data efficiently.
Key Takeaways:
- Excel can perform predictive modeling without complex coding
- The Analysis ToolPak is crucial for regression analysis in excel predictive analytics
- Interpreting R-squared, p-values, and coefficients is essential
- Linear regression in Excel can provide valuable business insights
Frequently Asked Questions
A. Yes, predictive modeling can be performed in Excel using tools like regression analysis, trendline fitting, and predictive functions. These tools help analyze data trends and make forecasts based on historical data.
A. To make predictions in Excel, utilize functions like FORECAST, TREND, or regression analysis tools. These functions analyze existing data trends and project future values based on established patterns.
A. Predictive modeling involves analyzing historical data to identify patterns and relationships. By using statistical techniques like regression analysis or machine learning algorithms, models are trained to make predictions on new data.
A. The formula for a predictive model depends on the specific technique used. For example, in linear regression, the formula to predict a dependent variable Y based on independent variables X1,X2,…,Xn is:
Y=β0+β1X1+β2X2+…+βnXn+ϵ









Thank you so much for all your articles. I read them regularly. Articles on Analyticsvidhya are the easiest to understand.
Thanks for the exposition. The application of the topics to real life examples have been very helpful.
Nicely crafted Ram. Thanks!
Hi admin.I really love your blog.Because your explanation wise all the topics are too good.I got enough knowledge from your blog.Thanks for sharing more. This blog contains a lot of knowledge. I think this is also helpful for the people. Keep sharing.
Your article is really good. I really appreciate it. I am looking for that type of article. That is very helpful for me. Thanks for sharing this. Keep sharing.
thank you very much to Mr.Ram Dewani for good explanation
Thank you, very helpful!
Dear Analytics Visdhya I wanted to thank you for sharing the article with me. I took the time to try out the predictive model you mentioned, and I have a few observations I would like to discuss. Firstly, I noticed that the accuracy of the model seems to be compromised even though you mentioned removing the "running Freq" field. I believe there might be some room for improvement in this area. Additionally, I found a discrepancy in the sample provided for prediction. The value mentioned in the article is 4218, but upon further analysis, I believe it should be 4216 instead. Please correct me if I am mistaken. I would greatly appreciate it if you could provide some clarification regarding these matters. Perhaps there are some additional steps or factors that need to be considered in order to obtain more accurate results from the predictive model. Thank you for your time and assistance. I look forward to hearing from you soon.