Complete Guide to Regularization Techniques in Machine Learning

This article was published as a part of the Data Science Blogathon

Introduction

One of the most common problems every Data Science practitioner faces is Overfitting. Have you tackled the situation where your machine learning model performed exceptionally well on the train data but was not able to predict on the unseen data or you were on the top of the competition in the public leaderboard, but your ranking drops by hundreds of places in the final rankings?

Well – this is the article for you!

Avoiding overfitting can single-handedly improve our model’s performance.

In this article, we will understand how regularization helps in overcoming the problem of overfitting and also increases the model interpretability.

This article is written under the assumption that you have a basic understanding of Regression models including Simple and Multiple linear regression, etc.

Table of Contents

• 👉 Why Regularization?
• 👉 What is Regularization?
• 👉 How does Regularization work?
• 👉 Techniques of Regularization
  • Ridge Regression
  • Lasso Regression
• 👉 Key differences between Ridge and Lasso Regression
• 👉 Mathematical Formulation of Regularization Techniques
• 👉 What does Regularization Achieve?

Why Regularization?

Sometimes what happens is that our Machine learning model performs well on the training data but does not perform well on the unseen or test data. It means the model is not able to predict the output or target column for the unseen data by introducing noise in the output, and hence the model is called an overfitted model.

Let’s understand the meaning of “Noise” in a brief manner:

By noise we mean those data points in the dataset which don’t really represent the true properties of your data, but only due to a random chance.

So, to deal with the problem of overfitting we take the help of regularization techniques.

What is Regularization?

• 👉 It is one of the most important concepts of machine learning. This technique prevents the model from overfitting by adding extra                      information to it.
• 👉 It is a form of regression that shrinks the coefficient estimates towards zero. In other words, this technique forces us not to learn a more            complex or flexible model, to avoid the problem of overfitting.
• 👉 Now, let’s understand the “How flexibility of a model is represented?”
•     For regression problems, the increase in flexibility of a model is represented by an increase in its coefficients, which are calculated              from the regression line.
• 👉 In simple words, “In the Regularization technique, we reduce the magnitude of the independent variables by keeping the same                number of variables”. It maintains accuracy as well as a generalization of the model.

How does Regularization Work?

Regularization works by adding a penalty or complexity term or shrinkage term with Residual Sum of Squares (RSS) to the complex model.

Let’s consider the Simple linear regression equation:

Here Y represents the dependent feature or response which is the learned relation. Then,

Y is approximated to β₀ + β₁X₁ + β₂X₂ + …+ β_pX_p

Here, X₁, X₂, …X_p are the independent features or predictors for Y, and

β₀, β₁,…..β_n represents the coefficients estimates for different variables or predictors(X), which describes the weights or magnitude attached to the features, respectively.

In simple linear regression, our optimization function or loss function is known as the residual sum of squares (RSS).

We choose those set of coefficients, such that the following loss function is minimized:

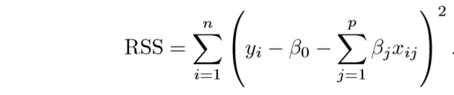
Fig. Cost Function For Simple Linear Regression

Image Source: link

Now, this will adjust the coefficient estimates based on the training data. If there is noise present in the training data, then the estimated coefficients won’t generalize well and are not able to predict the future data.

This is where regularization comes into the picture, which shrinks or regularizes these learned estimates towards zero, by adding a loss function with optimizing parameters to make a model that can predict the accurate value of Y.

Techniques of Regularization

Mainly, there are two types of regularization techniques, which are given below:

• Ridge Regression
• Lasso Regression

Ridge Regression

👉 Ridge regression is one of the types of linear regression in which we introduce a small amount of bias, known as Ridge regression penalty so that we can get better long-term predictions.

👉 In Statistics, it is known as the L-2 norm.

👉 In this technique, the cost function is altered by adding the penalty term (shrinkage term), which multiplies the lambda with the squared weight of each individual feature. Therefore, the optimization function(cost function) becomes:

 

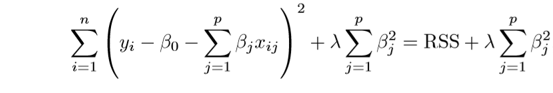
Fig. Cost Function for Ridge Regression

 

Image Source: link

In the above equation, the penalty term regularizes the coefficients of the model, and hence ridge regression reduces the magnitudes of the coefficients that help to decrease the complexity of the model.

👉 Usage of Ridge Regression:

• When we have the independent variables which are having high collinearity (problem of multicollinearity) between them, at that time general linear or polynomial regression will fail so to solve such problems, Ridge regression can be used.
• If we have more parameters than the samples, then Ridge regression helps to solve the problems.

👉 Limitation of Ridge Regression:

• Not helps in Feature Selection: It decreases the complexity of a model but does not reduce the number of independent variables since it never leads to a coefficient being zero rather only minimizes it. Hence, this technique is not good for feature selection.
• Model Interpretability: Its disadvantage is model interpretability since it will shrink the coefficients for least important predictors, very close to zero but it will never make them exactly zero. In other words, the final model will include all the independent variables, also known as predictors.

Lasso Regression

👉 Lasso regression is another variant of the regularization technique used to reduce the complexity of the model. It stands for Least Absolute and Selection Operator.

👉 It is similar to the Ridge Regression except that the penalty term includes the absolute weights instead of a square of weights. Therefore, the optimization function becomes:

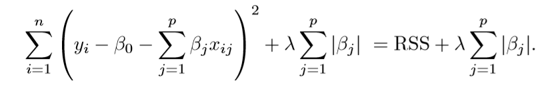
Fig. Cost Function for Lasso Regression

Image Source: link

👉 In statistics, it is known as the L-1 norm.

👉 In this technique, the L1 penalty has the effect of forcing some of the coefficient estimates to be exactly equal to zero which means there is a complete removal of some of the features for model evaluation when the tuning parameter λ is sufficiently large. Therefore, the lasso method also performs Feature selection and is said to yield sparse models.

👉 Limitation of Lasso Regression:

• Problems with some types of Dataset: If the number of predictors is greater than the number of data points, Lasso will pick at most n predictors as non-zero, even if all predictors are relevant.
• Multicollinearity Problem: If there are two or more highly collinear variables then LASSO regression selects one of them randomly which is not good for the interpretation of our model.

Key Differences between Ridge and Lasso Regression

👉 Ridge regression helps us to reduce only the overfitting in the model while keeping all the features present in the model. It reduces the complexity of the model by shrinking the coefficients whereas Lasso regression helps in reducing the problem of overfitting in the model as well as automatic feature selection.

👉 Lasso Regression tends to make coefficients to absolute zero whereas Ridge regression never sets the value of coefficient to absolute zero.

Mathematical Formulation of Regularization Techniques

👉 Now, we are trying to formulate these techniques in mathematical terms. So, these techniques can be understood as solving an equation,

For ridge regression, the total sum of squares of coefficients is less than or equal to s and for Lasso regression, the total sum of modulus of coefficients is less than or equal to s.

Here, s is a constant which exists for each value of the shrinkage factor λ.

These equations are also known as constraint functions.

👉 Let’s take an example to understand the mathematical formulation clearly,

For Example, Consider there are 2 parameters for a given problem

Ridge regression:

According to the above mathematical formulation, the ridge regression is described by β1² + β2² ≤ s.

This implies that ridge regression coefficients have the smallest RSS (loss function) for all points that lie within the circle given by β1² + β2² ≤ s.

Lasso Regression: 

According to the above mathematical formulation, the equation becomes,|β1|+|β2|≤ s.

This implies that the coefficients for lasso regression have the smallest RSS (loss function) for all points that lie within the diamond given by |β1|+|β2|≤ s.

The image below describes these equations:

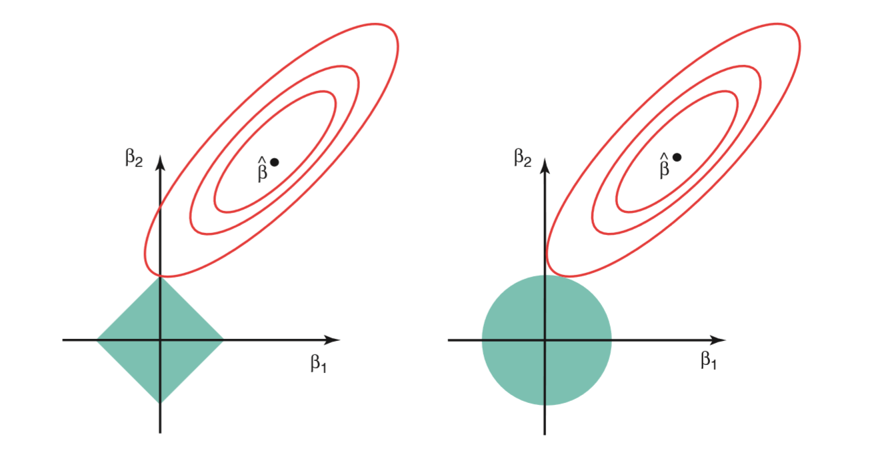
Image Source: link

Description About Image: The given image shows the constraint functions(in green areas), for lasso(in left) and ridge regression(in right), along with contours for RSS(red ellipse).

Points on the ellipse describe the value of Residual Sum of Squares (RSS) which is calculated for simple linear regression.

👉 For a very large value of s, the green regions will include the center of the ellipse with itself, which makes the coefficient estimates of both regression techniques equal to the least-squares estimates of simple linear regression. But, the given image shown does not describe this case. In that case, coefficient estimates of lasso and ridge regression are given by the first point at which an ellipse interacts with the constraint region.

Ridge Regression: Since ridge regression has a circular type constraint region, having no sharp points, so the intersection with the ellipse will not generally occur on the axes, therefore, the ridge regression coefficient estimates will be exclusively non-zero.

Lasso Regression: Lasso regression has a diamond type constraint region that has corners at each of the axes, so the ellipse will often intersect the constraint region at axes. When this happens, one of the coefficients (from collinear variables) will be zero and for higher dimensions having parameters greater than 2, many of the coefficient estimates may equal zero simultaneously.

What does Regularization achieve?

👉 In simple linear regression, the standard least-squares model tends to have some variance in it, i.e. this model won’t generalize well for a future data set that is different from its training data.

👉 Regularization tries to reduce the variance of the model, without a substantial increase in the bias.

👉 How λ relates to the principle of “Curse of Dimensionality”?

As the value of λ rises, it significantly reduces the value of coefficient estimates and thus reduces the variance. Till a point, this increase in λ is beneficial for our model as it is only reducing the variance (hence avoiding overfitting), without losing any important properties in the data. But after a certain value of λ, the model starts losing some important properties, giving rise to bias in the model and thus underfitting. Therefore, we have to select the value of λ carefully. To select the good value of λ, cross-validation comes in handy.

Important points about λ:

• λ is the tuning parameter used in regularization that decides how much we want to penalize the flexibility of our model i.e, controls the impact on bias and variance.
• When λ = 0, the penalty term has no effect, the equation becomes the cost function of the linear regression model. Hence, for the minimum value of λ i.e, λ=0, the model will resemble the linear regression model. So, the estimates produced by ridge regression will be equal to least squares.
• However, as λ→∞ (tends to infinity), the impact of the shrinkage penalty increases, and the ridge regression coefficient estimates will approach zero.

End Notes

Thanks for reading!

If you liked this and want to know more, go visit my other articles on Data Science and Machine Learning by clicking on the Link

Please feel free to contact me on Linkedin, Email.

Something not mentioned or want to share your thoughts? Feel free to comment below And I’ll get back to you.

About the author

Chirag Goyal

Currently, I am pursuing my Bachelor of Technology (B.Tech) in Computer Science and Engineering from the Indian Institute of Technology Jodhpur(IITJ). I am very enthusiastic about Machine learning, Deep Learning, and Artificial Intelligence.

The media shown in this article are not owned by Analytics Vidhya and is used at the Author’s discretion. 

Chirag Goyal

I am a B.Tech. student (Computer Science major) currently in the pre-final year of my undergrad. My interest lies in the field of Data Science and Machine Learning. I have been pursuing this interest and am eager to work more in these directions. I feel proud to share that I am one of the best students in my class who has a desire to learn many new things in my field.