This article was published as a part of the Data Science Blogathon
Introduction
Deep Neural Networks deal with a huge number of parameters for training and testing. As the number of parameters increases, neural networks have the freedom to fit different types of datasets which is what makes them so powerful. But, sometimes this power is what makes the neural network weak due to the problem of Overfitting.
To overcome Overfitting, there are a few techniques that can be used. So, In this article, we will be discussing the different techniques to avoid overfitting the model.
This is part-1 of two-part Blog Series on Regularization Techniques for Neural Networks.
Table of Contents
1. What is Overfitting?
2. Reasons for Overfitting
3. Why is Underfitting not widely discussed?
4. Techniques to Prevent Overfitting
- Decrease the Model Complexity
- Data Augmentation
- Weight Regularization
What is Overfitting?
The goal of deep learning models is to generalize well with the help of training data to any data from the problem domain. This is very crucial since we want our model to make predictions on the unseen dataset i.e, it has never seen before.
In Overfitting, the model tries to learn too many details in the training data along with the noise from the training data. As a result, the model performance is very poor on unseen or test datasets. Therefore, the network fails to generalize the features or patterns present in the training dataset.
How can we Spot the Overfitting while we Train our Model?
Overfitting during training can be spotted when the error on training data decreases to a very small value but the error on the new data or test data increases to a large value.
Now, let’s understand the Overfitting with the help of a given below plot:
Image Source: Google Images
This graph represents the error vs iteration curve that shows how a deep neural network overfits training data. Here, the blue curve represents the training error & the red curve represents the testing error. The point where the green line crosses is the point at which the network begins to overfit. As you can observe, the testing error increases sharply while the training error decreases.
Image Source: Google Images
Let’s understand the above diagram carefully:
The above figure, for a simple linear regression model, describes how the model tries to include every data point in the training set. So, when a new set of data points this will result in poor performance of the model as it is very close to all the training points which are noise & outliers. The error on the training points is minimal or very small but the error on the new data points will be high.
Reasons for Overfitting
The possible reasons for Overfitting in neural networks are as follows:
The size of the training dataset is small
When the network tries to learn from a small dataset it will tend to have greater control over the dataset & will make sure to satisfy all the data points exactly. So, the network is trying to memorize every single data point and failing to capture the general trend from the training dataset.
The model tries to make predictions on Noisy Data
Overfitting also occurs when the model tries to make predictions on data that is very noisy, which is caused due to an overly complex model having too many parameters. So, due to this, the overfitted model is inaccurate as the trend does not reflect the reality present in the data.
Why is Underfitting not widely discussed?
Underfitting happens when the network can neither model the training or test data which results in overall bad performance.
Underfitting happens in the first diagram i.e, on the left shown in the above picture. In that diagram, the model doesn’t cover all the data points & has a high error on both training & test data.
The reason for underfitting can be because of:
- The limited capacity of the network
- A smaller number of features provided as input to the network
- Noisy data, etc.
This phenomenon is not widely discussed as it is easy to detect & the remedy is to try different machine learning algorithms, provide more capacity to a deep neural network, remove noise from the input data, increase the training time, etc.
Reduce the Model Complexity
Let’s first understand:
Why Deep Neural Networks are prone to Overfitting?
Deep neural networks are prone to overfitting because they learn millions or billions of parameters while building the model. A model having this many parameters can overfit the training data because it has sufficient capacity to do so.
The basic idea to deal with the problem of overfitting is to decrease the complexity of the model. To do so, we can make the network smaller by simply removing the layers or reducing the number of neurons, etc.
Now, a question comes to mind:
How does Overfitting get reduced when we remove the layers or Reduce the Number of Neurons?
By removing some layers or reducing the number of neurons the network becomes less prone to overfitting as the neurons contributing to overfitting are removed or deactivated. Therefore, the network has a smaller number of parameters to learn because of which it cannot memorize all the data points & will be forced to generalize.
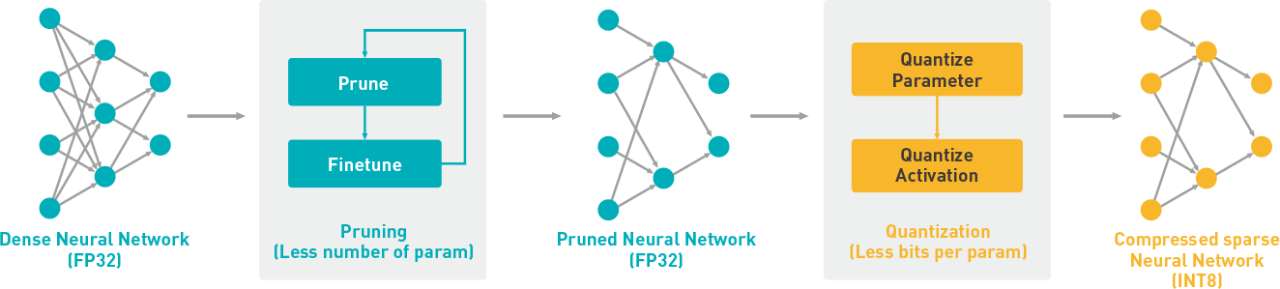
Image Source: Google Images
But while using this technique to resolve the issue, one has to keep in mind to compute the input and output dimensions of the various layers involved in the neural network.
While implementing this technique, we have to determine:
- How many layers to be removed
- How large your network should be
- How many neurons must be in a layer
There is no thumb of the rule to find the answer to the above questions, but there are some popular approaches to do this which are described below:
- Grid Search: Apply Grid search Cross-Validation to find out the number of neurons or layers to reduce.
- Trimming: We can also prune our overfitted model by removing nodes or connections until it reaches suitable performance on unseen datasets after model building.
So, In simple words in this technique, our aim is to make the neural network smaller to prevent it from overfitting.
Data Augmentation
One of the best techniques for reducing overfitting is to increase the size of the training dataset. As discussed in the previous technique, when the size of the training data is small, then the network tends to have greater control over the training data.
So, to increase the size of the training data i.e, increasing the number of images present in the dataset, we can use data augmentation, which is the easiest way to diversify our data and make the training data larger.
Some of the popular image augmentation techniques are flipping, translation, rotation, scaling, changing brightness, adding noise etcetera, etc.
But, Why are we focusing on Data Augmentation instead of collecting more data in step of Data Collection?
In real-world scenarios gathering large amounts of data is a tedious & time-consuming task, hence the collection of new data is not a viable option.
This technique is shown in the below diagram.
Image Source: Google Images
As we can see, using data augmentation, we can generate a lot of similar images, and the network is trained on multiple instances of the same class of objects from different perspectives. This helps in increasing the dataset size and thus reduces overfitting, as we add more and more data, the model is unable to overfit all the samples and is forced to generalize.
The images which we have got after applying the Data Augmentation will have an instance of a lion being viewed in:
- a rotated manner,
- a lion being viewed up-side-down, or
- cutting out the portion of an image that encloses the mane of a lion.
By applying the last augmentation (cutout) the network learns to associate the feature that male lions have a mane with their class.
Therefore, in simple words, the idea behind data augmentation is that by increasing the size of the training dataset, the network is unable to overfit all the training dataset (original images + augmented images) & thus is forced to generalize. But the overall training loss increases since the network doesn’t predict accurately on the augmented images thus increasing the training loss & the optimizer (optimization algorithm) tunes the network to capture the generalized trend present in the training dataset.
The graphical representation of the above discussion is as follow:
Before Data Augmentation
After Data Augmentation
Weight Regularization
This technique of reducing overfitting aims to stabilize an overfitted network by adding a weight penalty term, which penalizes the large value of weights in the network.
Usually, an overfitted model has problems with a large value of weights as a small change in the input can lead to large changes in the output.
Weight regularization penalizes the network’s large weights & forces the optimization algorithm to reduce the larger weight values to smaller weights, and this leads to stability of the network & presents good performance. In this technique, the network configuration remains unchanged since it only modifies the value of the weights.
Working Principle behind this Technique
It reduces overfitting by penalizing or adding a constraint to the loss function. Regularization terms are constraints the optimization algorithm (like Stochastic Gradient Descent) must adhere to when minimizing loss function apart from minimizing the error between predicted value & actual value.
Image Source: Google Images
The above two equations represent L1 & L2 Weight Regularization Techniques.
There are two components in the Regularized Equation:
- The first component represents the error between the actual target vs the predicted target (loss function).
- The second component represents the weight penalty or the regularization term.
Without the Regularization Term
If we don’t include the regularization term in the loss function, then the overall loss of the network is the same as the output of the loss function. When the network overfits on training data, the error between predicted & the actual value for training data is very small.
If the training error has a very small value, then the error gradient value is also very small. As a result, now change in weights are very small as,
new-weight = old-weight — lr*(error gradient)
As iteration is completed, the new weight value is close to the previous weight values, therefore the network still remains in the overfit condition.
With the Regularization Term
If we add a weight penalty to the loss function, then the overall loss/cost of the network increases. As a result, now the optimizer will force the network to minimize the weights as that is contributing more to the overall loss.
Also, if the error/loss increases, then the error gradient wrt weights also increases, which in turn results in a larger change in weight update whereas, without the weight penalty, the gradient value remains very small. So, the change in weights also remains small.
With an increase in the value of the error gradient, the large weight values are reduced to a smaller value in the weight update rule. So, larger values of weights result in a larger penalty to the loss function, thus pushing the network towards smaller and stabilized values of weights.
Types of Regularization
L1 regularization: In this regularization, the weight penalty we add is the sum of absolute values of the weights in the network.
L2 regularization: In this regularization, the weight penalty we add is the sum of squared values of the weights in the network.
Let’s see the difference between L1 and L2 Regularization:
Image Source: Google Images
For more details about L1 and L2 regularization, refer to the link.
Which Regularization Technique do we have to prefer?
L2 regularization is a better choice if the data is too complex, as it can model the inherent pattern in the data whereas L1 regularization can be used if the data is simple.
Therefore, the correct choice of regularization technique depends on the problem statement that we are trying to solve.
Test your knowledge
1. Which of the subsequent techniques doesn’t help us to scale back the overfitting while training a neural network?
- More availability of labels
- Data augmentation
- Increased data diversity
- Reduced model complexity
2. In the realm of neural networks, the concept of overfitting boils right down to the actual fact that the model is unable to
- Update its weights
- Predict well on the test data
- Learn well
- Generalize well
3. The general idea of data augmentation involves adding more data to the training set that’s almost like the data that we have already got but is simply reasonably modified to some extent in order that it isn’t the precise same.
- True
- False
4. One of the most effective techniques for reducing the overfitting of a neural network is to extend the complexity of the model so the model is more capable of extracting patterns within the data.
- True
- False
5. One way of reducing the complexity of a neural network is to get rid of a layer from the network.
- True
- False
End Notes
Thanks for reading!
If you liked this and want to know more, go visit my other articles on Data Science and Machine Learning by clicking on the Link
Please feel free to contact me on Linkedin, Email.
Something not mentioned or want to share your thoughts? Feel free to comment below And I’ll get back to you.
About the Author
Chirag Goyal
Currently, I am pursuing my Bachelor of Technology (B.Tech) in Computer Science and Engineering from the Indian Institute of Technology Jodhpur(IITJ). I am very enthusiastic about Machine learning, Deep Learning, and Artificial Intelligence.
The media shown in this article are not owned by Analytics Vidhya and are used at the Author’s discretion.
I am a B.Tech. student (Computer Science major) currently in the pre-final year of my undergrad. My interest lies in the field of Data Science and Machine Learning. I have been pursuing this interest and am eager to work more in these directions. I feel proud to share that I am one of the best students in my class who has a desire to learn many new things in my field.
