Interview Prep
Career
GenAI
Prompt Engg
ChatGPT
LLM
Langchain
RAG
AI Agents
Machine Learning
Deep Learning
GenAI Tools
LLMOps
Python
NLP
SQL
AIML Projects

Reading list

Machine Learning Basics for a Newbie
6 Steps of Machine learning Lifecycle Introduction to Predictive Modeling
Introduction to Exploratory Data Analysis & Data Insights Descriptive Statistics Inferential Statistics How to Understand Population Distributions?
Reading Data Files into Python Different Variable Datatypes
Probability for Data Science Basic Concepts of Probability Axioms of Probability Conditional Probability
Central Tendencies for Continuous Variables Spread of Data KDE plots for Continuous Variable Overview of Distribution for Continuous variables Normal Distribution Skewed Distribution Skeweness and Kurtosis Distribution for Continuous Variable
Central Tendencies for Categorical Variables Understanding Discrete Distributions Performing EDA on Categorical Variables
Dealing with Missing Values Understanding Outliers Identifying Outliers in Data Outlier Detection in Python Outliers Detection Using IQR, Z-score, LOF and DBSCAN
Sample and Population Central Limit Theorem Confidence Interval and Margin of Error
Bivariate Analysis Introduction
Covariance Pearson Correlation Spearman's Correlation & Kendall's Tau Correlation versus Causation Tabular and Graphical methods for Bivariate Analysis Performing Bivariate Analysis on Continuous-Continuous Variables
Tabular and Graphical methods for Continuous-Categorical Variables Introduction to Hypothesis Testing P-value Two sample Z-test T-test T-test vs Z-test Performing Bivariate Analysis on Continuous-Catagorical variables
Chi-Squares Test Bivariate Analysis on Categorical Categorical Variables
Multivariate Analysis A Comprehensive Guide to Data Exploration The Data Science behind IPL
Supervised Learning vs Unsupervised Learning Reinforcement Learning Generative and Descriminative Models Parametric and Non Parametric model
Machine Learning Pipeline Preparing Dataset Build a Benchmark Model: Regression Build a Benchmark Model: Classification
Evaluation Metrics for Machine Learning Everyone should know Confusion Matrix Accuracy Precision and Recall AUC-ROC Log Loss R2 and Adjusted R2
Dealing with Missing Values Replacing Missing Values Imputing Missing Values in Data Working with Categorical Variables Working with Outliers Preprocessing Data for Model Building
Understanding Cost Function Understanding Gradient Descent Math Behind Gradient Descent Assumptions of Linear Regression Implement Linear Regression from Scratch Train Linear Regression in Python Implementing Linear Regression in R Diagnosing Residual Plots in Linear Regression Models Generalized Linear Models Introduction to Logistic Regression Odds Ratio Implementing Logistic Regression from Scratch Introduction to Scikit-learn in Python Train Logistic Regression in python Multiclass using Logistic Regression How to use Multinomial and Ordinal Logistic Regression in R ? Challenges with Linear Regression Introduction to Regularisation Implementing Regularisation Ridge Regression Lasso Regression
Introduction to K Nearest Neighbours Determining the Right Value of K in KNN Implement KNN from Scratch Implement KNN in Python
Bias Variance Tradeoff Introduction to Overfitting and Underfitting Visualizing Overfitting and Underfitting Selecting the Right Model What is Validation? Hold-Out Validation Understanding K Fold Cross Validation
Introduction to Feature Selection Feature Selection Algorithms Missing Value Ratio Low Variance Filter High Correlation Filter Backward Feature Elimination Forward Feature Selection Implement Feature Selection in Python Implement Feature Selection in R
Introduction to Decision Tree Purity in Decision Tree Terminologies Related to Decision Tree How to Select Best Split Point in Decision Tree? Chi-Squares Information Gain Reduction in Variance Optimizing Performance of Decision Tree Train Decision Tree using Scikit Learn Pruning of Decision Trees
Introduction to Feature Engineering Feature Transformation Feature Scaling Feature Engineering Frequency Encoding Automated Feature Engineering: Feature Tools
Introduction to Naive Bayes Conditional Probability and Bayes Theorem Introduction to Bayesian Adjustment Rating: The Incredible Concept Behind Online Ratings! Working of Naive Bayes Math behind Naive Bayes Types of Naive Bayes Implementation of Naive Bayes
Understanding how to solve Multiclass and Multilabled Classification Problem Evaluation Metrics: Multi Class Classification
Introduction to Ensemble Techniques Basic Ensemble Techniques Implementing Basic Ensemble Techniques Finding Optimal Weights of Ensemble Learner using Neural Network Why Ensemble Models Work well?
Introduction to Stacking Implementing Stacking Variants of Stacking Implementing Variants of Stacking Introduction to Blending Bootstrap Sampling Introduction to Random Sampling Hyper-parameters of Random Forest Implementing Random Forest Out-of-Bag (OOB) Score in the Random Forest IPL Team Win Prediction Project Using Machine Learning Introduction to Boosting Gradient Boosting Algorithm Math behind GBM Implementing GBM in python Regularized Greedy Forests Extreme Gradient Boosting Implementing XGBM in python Tuning Hyperparameters of XGBoost in Python Implement XGBM in R/H2O Adaptive Boosting Implementing Adaptive Boosing LightGBM Implementing LightGBM in Python Catboost Implementing Catboost in Python
Different Hyperparameter Tuning methods Implementing Different Hyperparameter Tuning methods GridsearchCV RandomizedsearchCV Bayesian Optimization for Hyperparameter Tuning Hyperopt
Understanding SVM Algorithm SVM Kernels In-depth Intuition and Practical Implementation SVM Kernel Tricks Kernels and Hyperparameters in SVM Implementing SVM from Scratch in Python and R
Introduction to Principal Component Analysis Steps to Perform Principal Compound Analysis Computation of Covariance Matrix Finding Eigenvectors and Eigenvalues Implementing PCA in python Visualizing PCA A Brief Introduction to Linear Discriminant Analysis Introduction to Factor Analysis
Introduction to Clustering Applications of Clustering Evaluation Metrics for Clustering Understanding K-Means Implementation of K-Means in Python Implementation of K-Means in R Choosing Right Value for K Profiling Market Segments using K-Means Clustering Hierarchical Clustering Implementation of Hierarchial Clustering DBSCAN Defining Similarity between clusters Build Better and Accurate Clusters with Gaussian Mixture Models
Understand Basics of Recommendation Engine with Case Study
8 Ways to Improve Accuracy of Machine Learning Models
Introduction to Dask Working with CuML
Introduction to Machine Learning Interpretability Framework and Interpretable Models model Agnostic Methods for Interpretability Implementing Interpretable Model Understanding SHAP Out-of-Core ML Introduction to Interpretable Machine Learning Models Model Agnostic Methods for Interpretability Game Theory & Shapley Values
Introduction to Machine Learning Interpretability Framework and Interpretable Models model Agnostic Methods for Interpretability Implementing Interpretable Model Understanding SHAP Out-of-Core ML Introduction to Interpretable Machine Learning Models Model Agnostic Methods for Interpretability Game Theory & Shapley Values
Introduction to AutoML Implementation of MLBox Introduction to PyCaret TPOT Auto-Sklearn EvalML
Pickle and Joblib Introduction to Model Deployment
Deploying Machine Learning Model using Streamlit Deploying ML Models in Docker Deploy Using Streamlit Deploy on Heroku Deploy Using Netlify Introduction to Amazon Sagemaker Setting up Amazon SageMaker Using SageMaker Endpoint to Generate Inference Deploy on Microsoft Azure Cloud Introduction to Flask for Model Deploying ML model using Flask
Model Deployment in Android Model Deployment in Iphone

Solve a business case using simple Markov Chain

Tavish Srivastava
Tavish Srivastava Last Updated : 17 Apr, 2015
5 min read

Markov process fits into many real life scenarios. Any sequence of event that can be approximated by Markov chain assumption, can be predicted using Markov chain algorithm. In the last article, we explained What is a Markov chain and how can we represent it graphically or using Matrices. In this article, we will go a step further and leverage this technique to draw useful business inferences.

[stextbox id=”section”] Business Case [/stextbox]

“Krazy Bank”, deals with both asset and liability products in retail bank industry. A big portfolio of the bank is based on loans. These loans make the majority of the total revenue earned by the bank. Hence, it is very essential for the bank to find the proportion of loans which have a high propensity to be paid in full and those which will finally become Bad loans. “Krazy Bank” has hired you as a consultant to come up with these scoping numbers.

All the loans, which have been issued by “Krazy Bank” can be classified into four categories :

  1. Good Loans : These are the loans which are in progress but are given to low risk customers. We expect most of these loans will be paid up in full with time.
  2. Risky loans : These are also the loans which are in progress but are given to medium or high risk customers. We expect a good number of these customers will default.
  3. Bad loans : The customer to whom these loans were given have already defaulted.
  4. Paid up loans : These loans have already been paid in full.

 

[stextbox id=”section”] Short Note on Absorbing nodes [/stextbox]

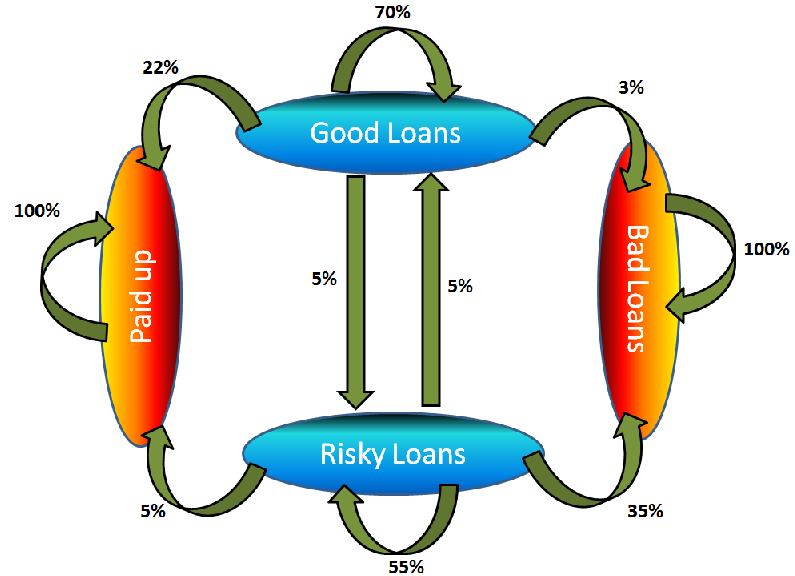
Absorbing nodes in a Markov chain are the possible end states. All nodes in Markov chain have an array of transitional probability to all other nodes and themselves. But, absorbing nodes have no transitional probability to any other node. Hence, if any individual lands up to this state, he will stick to this node for ever. Let’s take a simple example. We are making a Markov chain for a bill which is being passed in parliament house. It has a sequence of steps to follow, but the end states are always either it becomes a law or it is scrapped. These two are said to be absorbing nodes. For the loans example, bad loans and paid up loans are end states and hence absorbing nodes.

 

[stextbox id=”section”] Transition diagram [/stextbox]

You have done a thorough research on past trends of loan cycle and based on past trends here is the Markov chain you observed (for a period of 1 year):

cycle

Explaining absorbing nodes becomes simple from this diagram. As you can see, Paid up and bad loans transition only to themselves. Hence, whatever path a process takes, if it lands up to one of these two states, it will stay there for ever. In other words, a bad loan cannot become paid up, risky or good loan ever after. Same is true with paid up loans.

[stextbox id=”section”] Transition calculations [/stextbox]

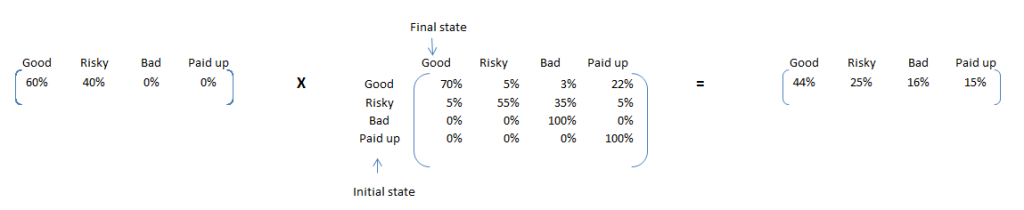
Once, we have  1 year transition probability, we can convert prediction algorithm to simple matrix multiplication. Currently the portfolio has 60% Good and 40% Risky loans. We look forward to calculate, how many of these loans will be finally paid up in full? Using 1 year transition probability, we can estimate the number of loans falling into each of the four bucket 1 year down the line.

trans3

Here are some interesting insights from this calculation. We can expect 15% of the loans to be paid up in this year and 16% being ending up as bad loans. As the % of bad loans seem to be on a higher side, it will be beneficial to identify these loans and make adequate interventions. Pin pointing to these 15% is not possible using simple Markov chain, but same is possible using a Latent Markov model.

Now, to make a prediction for 2 years, we can use the same transition matrix. This time the initial proportions will the final proportions of last calculation. Transition probability generally do not change much. This is because, it is based on several time points in past.

trans4

 If we keep on repeating this exercise, we see the proportion matrix converges. Following is the converged matrix. Note that, multiplying it with transition matrix makes no change to proportions.

trans5

These are the proportion numbers we were looking for. 54% of the current loans will be paid up in full but 46% will default. Hence doing this simple exercise lead us to such an important conclusion that the current portfolio exposes bank to a very high risk.

[stextbox id=”section”] Loan transition deep dive  [/stextbox]

We have already seen the stationary point proportions for the portfolio. Something which will be of interest to us next is that what proportion of Good loans land up being paid up in full. For this we can start with an initial proportion split of Good – 100% and rest – 0%. The final converged matrix is as follows:

trans6

Here are some interesting insights. If the entire portfolio was built of good loans, only 23% of loans would have defaulted against 46% for current portfolio. Hence, we will expect a very high proportion of risky loans will show default. We can find this using a simple transition calculation using Risky – 100% and rest – 0%. Following is the final converged matrix :

trans7

 

80% of such loans will default. Hence, our classification of Risky and Good separates out propensity to default pretty nicely.

[stextbox id=”section”] End Notes  [/stextbox]

In this article, we saw how Markov chain can be used to find out multiple insights and make good predictions on an overall level. There are many other processes which can be explained using Markov chain. In such cases, Markov chain algorithm will give you number of insights and will serve as a very handy forecasting tool. However, Markov chain can only make forecast on segment level and not make prediction on customer level. In case you need to make customer level forecast, you need a Latent Markov model and not a simple Markov model.

Did you find the article useful? Are you aware of any other real life Markov process? Can Markov chain be used in that process to bring out interesting insights? Did this article solve any of your existing problems? Have you used simple Markov chain in any other context ?

If you like what you just read & want to continue your analytics learning, subscribe to our emails, follow us on twitter or like our facebook page.

 

Tavish Srivastava
Tavish Srivastava

Tavish Srivastava, co-founder and Chief Strategy Officer of Analytics Vidhya, is an IIT Madras graduate and a passionate data-science professional with 8+ years of diverse experience in markets including the US, India and Singapore, domains including Digital Acquisitions, Customer Servicing and Customer Management, and industry including Retail Banking, Credit Cards and Insurance. He is fascinated by the idea of artificial intelligence inspired by human intelligence and enjoys every discussion, theory or even movie related to this idea.

Free Courses

Generative AI 4.7

Generative AI - A Way of Life

Explore Generative AI for beginners: create text and images, use top AI tools, learn practical skills, and ethics.
Large Language Models 4.5

Getting Started with Large Language Models

Master Large Language Models (LLMs) with this course, offering clear guidance in NLP and model training made simple.
Prompt Engineering 4.6

Building LLM Applications using Prompt Engineering

This free course guides you on building LLM apps, mastering prompt engineering, and developing chatbots with enterprise data.
LlamaIndex 4.8

Improving Real World RAG Systems: Key Challenges & Practical Solutions

Explore practical solutions, advanced retrieval strategies, and agentic RAG systems to improve context, relevance, and accuracy in AI-driven applications.
RAG systems using LlamaIndex 4.7

Microsoft Excel: Formulas & Functions

Master MS Excel for data analysis with key formulas, functions, and LookUp tools in this comprehensive course.

Recommended Articles

Responses From Readers

Clear

pradeep
pradeep

Hi Tavish, Thank you for sharing this. It's interesting and very useful. I have one clarification how do we get the "Final state transition matrix" 4x4 matrix?. Sorry if i am missing something here. Regards, S.S.Pradeep

123

Tavish Srivastava
Tavish Srivastava

Pradeep, The case discussed in this article has a constant transition probability matrix. Do you can use the same matrix throughout. Tavish

123
Koushik Kar
Koushik Kar

Hi Tavish, I have recently enrolled for a course in BA and trying to grasp as much information as possible. This Markov Chain problem correlates with some of the current issues in my Organization. Waiting for your future publications. Thanks & Regards, Koushik

123

Tavish Srivastava
Tavish Srivastava

Koushik, Can you illustrate the problem you are referring to?

123
uday
uday

Tavish this is interesting. can you elaborate on the deeep dive section.. how you arrived at the final converged matrix You mention "For this we can start with an initial proportion split of Good – 100% and rest – 0%. " So would the initial matrix be good risky bad paid up [100 0 0 0] If that is the initial matrix how do you arrive at good risky bad paid up [0 0 23 76] Thanks for your papers. they are very good for novices like me. Uday

123

Tavish Srivastava
Tavish Srivastava

Uday, The converged matrix is found by multiplying the transition matrix many times to the the current state. This is basically the final proportion of state distribution. You are right the initial matrix will be [100 0 0 0]. Keep on multiplying the transition matrix to this matrix and you will get [0 0 23 76]. Hope this helps. Tavish

123

Write for us

Write, captivate, and earn accolades and rewards for your work
  • Reach a Global Audience
  • Get Expert Feedback
  • Build Your Brand & Audience
  • Cash In on Your Knowledge
  • Join a Thriving Community
  • Level Up Your Data Science Game
imag

We use cookies essential for this site to function well. Please click to help us improve its usefulness with additional cookies. Learn about our use of cookies in our Privacy Policy & Cookies Policy.

Show details