How to interpret hidden state in Latent Markov Model

In some of my previous articles, I have illustrated how Markov model can be used in real life forecasting problems. As described in these articles, Simple Markov model cannot be used for customer level predictions, because it does not take into account any covariates for predictions. Latent Markov model is a modified version of the same Markov chain formulation, which can be leveraged for customer level predictions. “Latent” in this name is a representation of “Hidden states”. In this article, our focus will not be on how to formulate a Latent Markov model but simply on what do these hidden state actually mean. This is a concept which I have found quite ambiguous in the web world and too much statistics to understand this simple concept. In this article, I will try to illustrate physical interpretation of this concept “Hidden state” using a simple example.

[stextbox id=”section”] Case Background [/stextbox]

A prisoner was trying to escape from the prison. He was told that he will be sent a help from outside the prison, the first day when it rains. But, he was caught having a fight with his cellmate and sentenced for stay in a dark cell for a day. He is good with probabilities and will like to make inference about the weather outside. In case he gets a probability more than 50% of the day being rainy, he will make a move else will not attract attention unnecessarily. The only clue he gets in the dark cell is the accessories, which the policeman carries while coming to the cell. Given that the policeman carries Food plate wrapped in polythene 25% of times, Food plate in packed container 25% times and open food plate 50% of times; what is the probability that it will rain the same day when the prisoner is in the dark cell?

[stextbox id=”section”] Using case to build analogies [/stextbox]

In this case we have two key events. First event is “what accessories does the policeman carry” and second event is that “it will rain on the day when the prisoner is in the dark cell”.

[stextbox id=”grey”]

What accessories does the policeman carry : Observation or Ownership

it will rain on the day when the prisoner is in the dark cell : Hidden state

[/stextbox]

Hidden state and Ownership are commonly used terms in LMM model. As you can see that the observation is something the prisoner can see and accurately determine at any point of time. But the event of raining the day when he is in dark cell is something which he can only infer and not state with 100% accuracy.

[stextbox id=”section”] Calculations [/stextbox]

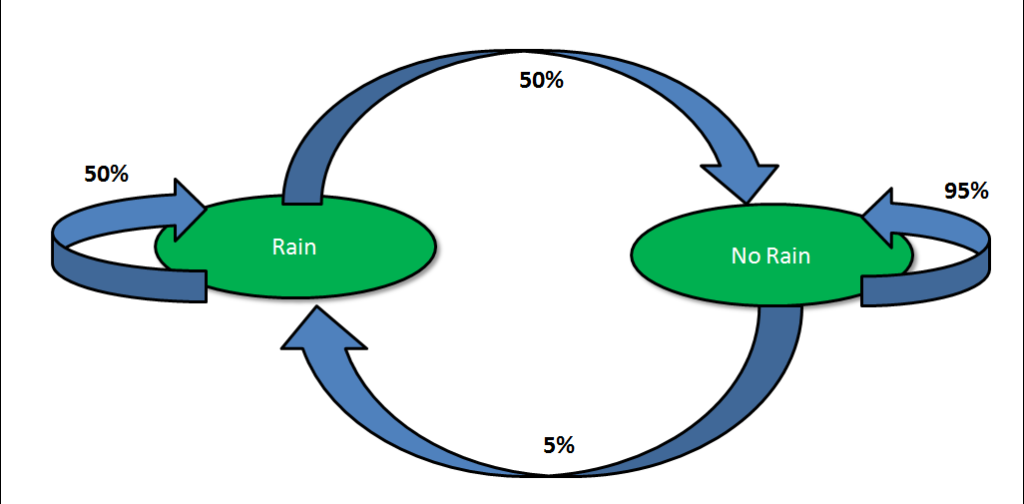
Having understood the concept of hidden states, let’s crunch some numbers to come up with the final probability of it raining on the day prisoner is in the dark cell. Prisoner being anxious for last few days about the weather was noting the weather for last few months. Based on these sequence, he has make a Markov chain for the weather next day given the weather of that day. Following is how the chain looks like :

The prisoner knows that it didn’t rain yesterday (Obviously, otherwise he would not have been in jail anymore). If he uses the Markov chain directly, he can conclude with some accuracy whether it will rain today or not. Following is the formulation for such a calculation :

[stextbox id=”grey”]

P(Rain today/No Rain yesterday)= 5%

[/stextbox]

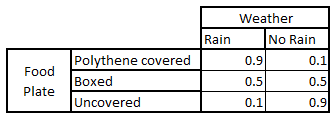
Hence, the chances seem really low that it is raining out today. Now, let’s bring in some amount of information on the observation or ownership. Using some good judgement, the prisoner already knows the following conditional probability Matrix :

Let’s take one cell to clarify the grid. The chances are 90% that it is raining today if we already know that the policeman is carrying the food plate with a polythene without taking into account the weather of last day. The prisoner is keenly waiting for the policeman to come and give the final clue to determine the final set of probability. The policeman actually brings in food with a polythene. Before making calculations, let’s first decide the set of events.

[stextbox id=”grey”]

A : It will rain today

B: It did not rain yesterday

C: The  policeman brings in food with a polythene

[/stextbox]

What we want to calculate is P(A/B,C)? Now let’s look at the set of probabilities we know :

[stextbox id=”grey”]

P(A/B) = 5%         P(C/A) = 90%      P(C) = 25%

[/stextbox]

We now will convert the expression P(A/B,C) into these know 3 parameters.

[stextbox id=”grey”]

P(A/B,C) = P(A,B/C)/P(B/C) = P(A,B/C)/P(B) {Using Markov first order principle} …………………………1

P(A,B/C) = P(A,B,C)/P(C) = P(C/A,B)*P(A,B)/P(C) = P(C/A)*P(A,B)/P(C) {Using Markov first order principle}

=> P(A,B/C) = P(C/A) * P(A/B)*P(B)/P(C)

Substituting this in equation 1,

P(A/B,C) = P(C/A) * P(A/B) / P(C) = 90%*5%/25% = 18%

[/stextbox]

[stextbox id=”section”] Final inferences [/stextbox]

P(It will rain today/no rain yesterday,policeman brings in food with a polythene) = 18%

As you can see, this probability is between 5% and 90% as estimated  separately by the two clues we have for prediction. Combination of both the clues reveals a more accurate prediction of the event in focus. Because this probability is less than 50%, the prisoner will not take a chance expecting a rain today.

[stextbox id=”section”] End Notes [/stextbox]

Using Markov chain simplifications , observations and Markov chain transition probability we were able to find out the hidden state for the day when prisoner was in the dark cell. The scope of this article was restricted to understanding hidden states and not framework of Latent Markov model. In some of the future article we will also touch up on formulation of Latent Markov model and its applications.

Did you find the article useful? Did this article solve any of your existing dilemmas? If you did, share with us your thoughts on the topic.

If you like what you just read & want to continue your analytics learning, subscribe to our emails, follow us on twitter or like our facebook page.

Tavish Srivastava

Tavish Srivastava, co-founder and Chief Strategy Officer of Analytics Vidhya, is an IIT Madras graduate and a passionate data-science professional with 8+ years of diverse experience in markets including the US, India and Singapore, domains including Digital Acquisitions, Customer Servicing and Customer Management, and industry including Retail Banking, Credit Cards and Insurance. He is fascinated by the idea of artificial intelligence inspired by human intelligence and enjoys every discussion, theory or even movie related to this idea.