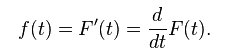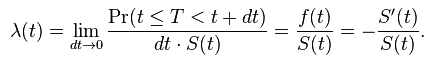Interview Prep
Career
GenAI
Prompt Engg
ChatGPT
LLM
Langchain
RAG
AI Agents
Machine Learning
Deep Learning
GenAI Tools
LLMOps
Python
NLP
SQL
AIML Projects

Reading list

Machine Learning Basics for a Newbie
6 Steps of Machine learning Lifecycle Introduction to Predictive Modeling
Introduction to Exploratory Data Analysis & Data Insights Descriptive Statistics Inferential Statistics How to Understand Population Distributions?
Reading Data Files into Python Different Variable Datatypes
Probability for Data Science Basic Concepts of Probability Axioms of Probability Conditional Probability
Central Tendencies for Continuous Variables Spread of Data KDE plots for Continuous Variable Overview of Distribution for Continuous variables Normal Distribution Skewed Distribution Skeweness and Kurtosis Distribution for Continuous Variable
Central Tendencies for Categorical Variables Understanding Discrete Distributions Performing EDA on Categorical Variables
Dealing with Missing Values Understanding Outliers Identifying Outliers in Data Outlier Detection in Python Outliers Detection Using IQR, Z-score, LOF and DBSCAN
Sample and Population Central Limit Theorem Confidence Interval and Margin of Error
Bivariate Analysis Introduction
Covariance Pearson Correlation Spearman's Correlation & Kendall's Tau Correlation versus Causation Tabular and Graphical methods for Bivariate Analysis Performing Bivariate Analysis on Continuous-Continuous Variables
Tabular and Graphical methods for Continuous-Categorical Variables Introduction to Hypothesis Testing P-value Two sample Z-test T-test T-test vs Z-test Performing Bivariate Analysis on Continuous-Catagorical variables
Chi-Squares Test Bivariate Analysis on Categorical Categorical Variables
Multivariate Analysis A Comprehensive Guide to Data Exploration The Data Science behind IPL
Supervised Learning vs Unsupervised Learning Reinforcement Learning Generative and Descriminative Models Parametric and Non Parametric model
Machine Learning Pipeline Preparing Dataset Build a Benchmark Model: Regression Build a Benchmark Model: Classification
Evaluation Metrics for Machine Learning Everyone should know Confusion Matrix Accuracy Precision and Recall AUC-ROC Log Loss R2 and Adjusted R2
Dealing with Missing Values Replacing Missing Values Imputing Missing Values in Data Working with Categorical Variables Working with Outliers Preprocessing Data for Model Building
Understanding Cost Function Understanding Gradient Descent Math Behind Gradient Descent Assumptions of Linear Regression Implement Linear Regression from Scratch Train Linear Regression in Python Implementing Linear Regression in R Diagnosing Residual Plots in Linear Regression Models Generalized Linear Models Introduction to Logistic Regression Odds Ratio Implementing Logistic Regression from Scratch Introduction to Scikit-learn in Python Train Logistic Regression in python Multiclass using Logistic Regression How to use Multinomial and Ordinal Logistic Regression in R ? Challenges with Linear Regression Introduction to Regularisation Implementing Regularisation Ridge Regression Lasso Regression
Introduction to K Nearest Neighbours Determining the Right Value of K in KNN Implement KNN from Scratch Implement KNN in Python
Bias Variance Tradeoff Introduction to Overfitting and Underfitting Visualizing Overfitting and Underfitting Selecting the Right Model What is Validation? Hold-Out Validation Understanding K Fold Cross Validation
Introduction to Feature Selection Feature Selection Algorithms Missing Value Ratio Low Variance Filter High Correlation Filter Backward Feature Elimination Forward Feature Selection Implement Feature Selection in Python Implement Feature Selection in R
Introduction to Decision Tree Purity in Decision Tree Terminologies Related to Decision Tree How to Select Best Split Point in Decision Tree? Chi-Squares Information Gain Reduction in Variance Optimizing Performance of Decision Tree Train Decision Tree using Scikit Learn Pruning of Decision Trees
Introduction to Feature Engineering Feature Transformation Feature Scaling Feature Engineering Frequency Encoding Automated Feature Engineering: Feature Tools
Introduction to Naive Bayes Conditional Probability and Bayes Theorem Introduction to Bayesian Adjustment Rating: The Incredible Concept Behind Online Ratings! Working of Naive Bayes Math behind Naive Bayes Types of Naive Bayes Implementation of Naive Bayes
Understanding how to solve Multiclass and Multilabled Classification Problem Evaluation Metrics: Multi Class Classification
Introduction to Ensemble Techniques Basic Ensemble Techniques Implementing Basic Ensemble Techniques Finding Optimal Weights of Ensemble Learner using Neural Network Why Ensemble Models Work well?
Introduction to Stacking Implementing Stacking Variants of Stacking Implementing Variants of Stacking Introduction to Blending Bootstrap Sampling Introduction to Random Sampling Hyper-parameters of Random Forest Implementing Random Forest Out-of-Bag (OOB) Score in the Random Forest IPL Team Win Prediction Project Using Machine Learning Introduction to Boosting Gradient Boosting Algorithm Math behind GBM Implementing GBM in python Regularized Greedy Forests Extreme Gradient Boosting Implementing XGBM in python Tuning Hyperparameters of XGBoost in Python Implement XGBM in R/H2O Adaptive Boosting Implementing Adaptive Boosing LightGBM Implementing LightGBM in Python Catboost Implementing Catboost in Python
Different Hyperparameter Tuning methods Implementing Different Hyperparameter Tuning methods GridsearchCV RandomizedsearchCV Bayesian Optimization for Hyperparameter Tuning Hyperopt
Understanding SVM Algorithm SVM Kernels In-depth Intuition and Practical Implementation SVM Kernel Tricks Kernels and Hyperparameters in SVM Implementing SVM from Scratch in Python and R
Introduction to Principal Component Analysis Steps to Perform Principal Compound Analysis Computation of Covariance Matrix Finding Eigenvectors and Eigenvalues Implementing PCA in python Visualizing PCA A Brief Introduction to Linear Discriminant Analysis Introduction to Factor Analysis
Introduction to Clustering Applications of Clustering Evaluation Metrics for Clustering Understanding K-Means Implementation of K-Means in Python Implementation of K-Means in R Choosing Right Value for K Profiling Market Segments using K-Means Clustering Hierarchical Clustering Implementation of Hierarchial Clustering DBSCAN Defining Similarity between clusters Build Better and Accurate Clusters with Gaussian Mixture Models
Understand Basics of Recommendation Engine with Case Study
8 Ways to Improve Accuracy of Machine Learning Models
Introduction to Dask Working with CuML
Introduction to Machine Learning Interpretability Framework and Interpretable Models model Agnostic Methods for Interpretability Implementing Interpretable Model Understanding SHAP Out-of-Core ML Introduction to Interpretable Machine Learning Models Model Agnostic Methods for Interpretability Game Theory & Shapley Values
Introduction to Machine Learning Interpretability Framework and Interpretable Models model Agnostic Methods for Interpretability Implementing Interpretable Model Understanding SHAP Out-of-Core ML Introduction to Interpretable Machine Learning Models Model Agnostic Methods for Interpretability Game Theory & Shapley Values
Introduction to AutoML Implementation of MLBox Introduction to PyCaret TPOT Auto-Sklearn EvalML
Pickle and Joblib Introduction to Model Deployment
Deploying Machine Learning Model using Streamlit Deploying ML Models in Docker Deploy Using Streamlit Deploy on Heroku Deploy Using Netlify Introduction to Amazon Sagemaker Setting up Amazon SageMaker Using SageMaker Endpoint to Generate Inference Deploy on Microsoft Azure Cloud Introduction to Flask for Model Deploying ML model using Flask
Model Deployment in Android Model Deployment in Iphone

A Comprehensive guide to Parametric Survival Analysis

Tavish Srivastava
Tavish Srivastava Last Updated : 26 Jun, 2020
7 min read

Introduction

Survival analysis is one of the less understood and highly applied algorithm by business analysts. That is a dangerous combination! Not many analysts understand the science and application of survival analysis, but because of its natural use cases in multiple scenarios, it is difficult to avoid!

P.S. If you read the first half of this article last week, you can jump here. We have combined the articles to make it more useful for our readers.

Survival analysis refers to analyzing a set of data in a defined time duration before another event occurs. The number of years in which a human can get affected by diabetes / heart attack is a quintessential of survival analysis. Survival analysis is one of the most used algorithms, especially in Pharmaceutical industry.

In one of the previous article, we have already discussed the use cases of survival analysis. We also talked about non-parametric and semi-parametric survival analysis. We suggest you to go through these articles first to get a good understanding of this article.

In this article, you will learn:

  1. The basics of Parametric analysis to derive detailed and actionable insights from a Survival analysis.
  2. How to find the right distribution in a parametric survival model?
  3. Different functions used in parametric survival model followed by their applications.

Let us first understand how various types of Survival analysis differ from each other.

 

Basics of Survival analysis

A survival analysis is different from traditional model like regression and classification problems as it models two different parameters. To understand the Survival analysis in detail, refer to our previous articles(1 & 2). However, in this article we will also discuss how the three types of analysis are different from each other.

surv

The image above will help you understand the difference between the three classes of Survival analysis models. Having already explained about semi parametric models, we will go a step ahead and understand how to build a Parametric model.

In a parametric model, we assume the distribution of the survival curve. Even before fitting a model, you need to know the shape of the Survival curve and the best function which will fit in this shape. For this you need to build a non-parametric model and understand the shape of hazard function and the survival curve.

 

What are the distributions used in Parametric Models?

There are five types of distribution of Survival/hazard functions which are frequently assumed while doing a survival analysis. The name of each of these distribution comes from the type of probability distribution of the failure function. Following are the 5 types of probability distribution curve generally used in parametric models. Each distribution been explained below in detail:

  1. Normal Distribution
  2. Uniform Distribution
  3. Exponential Distribution
  4. Weibull Distribution
  5. Lognormal Distribution

 

For each of these distributions, let’s first understand the following plots :

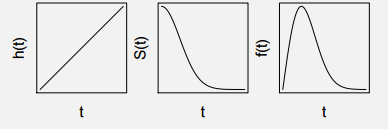
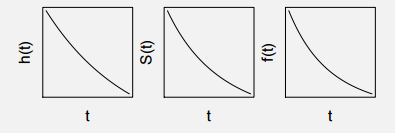
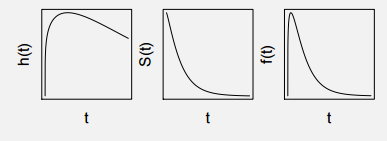
1. Lifetime Distribution Function (F) : This is the probability of failure happening before a time ‘T’.

lifetime

 

 

2. Lifetime Probability distribution (f) : A differential of F will give us probability distribution. All the names of distribution function is based on this probability distribution.

lifetime distr

 

3. Survival Function (S) : Survival is the inverse of Lifetime. It is one minus Lifetime distribution.

survival

 

4. Hazard Function (Lambda) : Hazard function is the rate of event happening. Hazard function can be derived from the Survival function as follows :

hazard

 

5. Cumulative Hazard Function : This is simply the integral of the hazard function and is given as below :

sumhaz

 

Also, by integrating the hazard function equation we get following equation :

sumhaz1

 

Following are the two plots we will refer in each case (these are the important ones to select the distribution) :

a. Hazard Function

b. Survival Function

 

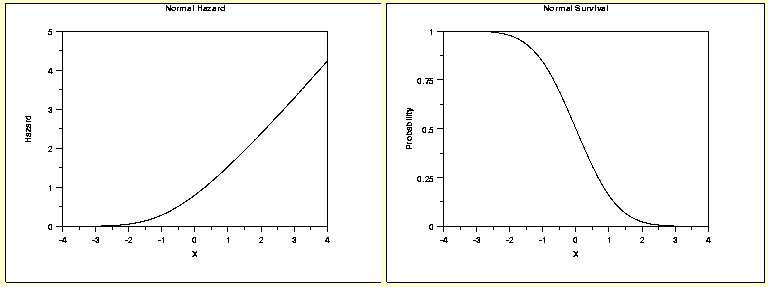
1. Normal Distribution

This type of distribution is assumed when the risk of failure increases considerably with time. Hence, the probability of failure increases suddenly. Check the graphs shown below:

normal

 

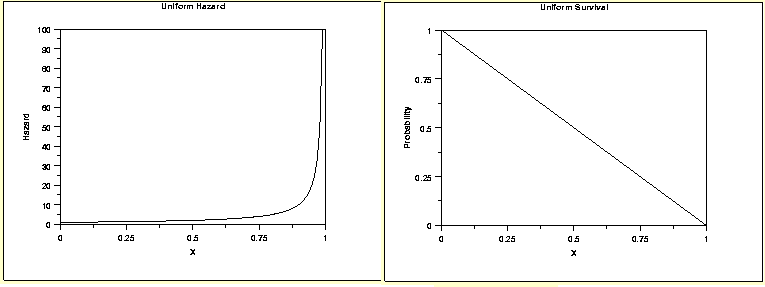
2. Uniform distribution

Uniform distribution is not a common type to be assumed in real world. The survival curve is just a straight line from 100% to 0%. And the hazard function increases exponentially to force death of every single observation towards the end. Check the graphs shown below:

uniform

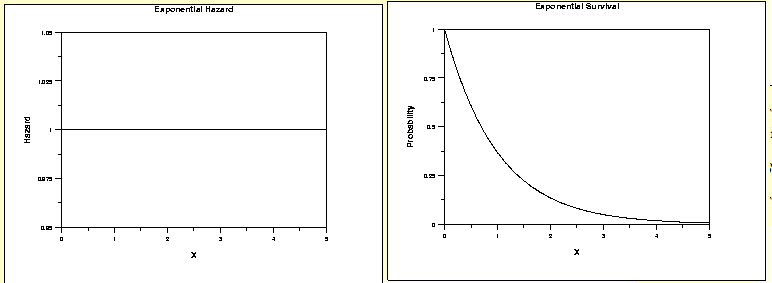
3. Exponential Distribution

Exponential distribution is one of the common assumption taken in survival models. The hazard function does not vary with time. This distribution can be assumed in case of natural death of human beings where the rate does not vary much over time. Check the graphs shown below:

exp

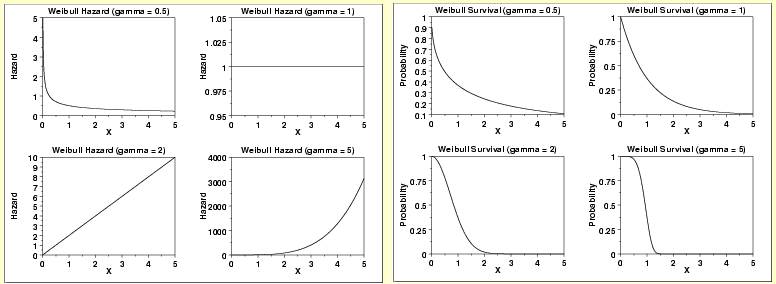
4. Weibull Distribution

Weibull distribution has a parameter gamma which can be optimized to get different distributions of hazard function. Following are a few scenarios which will illustrate the same:

weibull

As you can see from the multiple scenarios, gamma can change the weibull hazard function from steep decline to constant function to accelerating increase. Hence, it fits into multiple situations in our practical world.

 

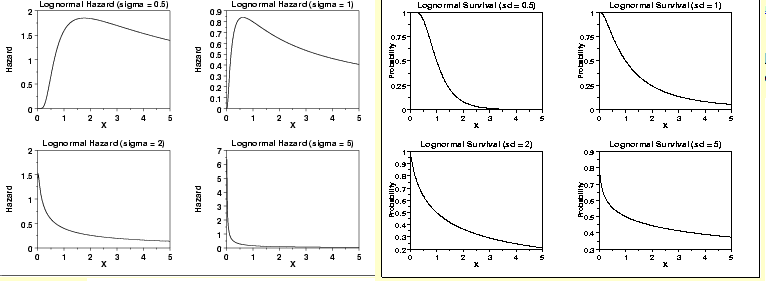
5. Log-normal Distribution

Here is another distribution which can be optimized for different hazard functions. Lognormal distribution can be complimented by Weibull distribution to simulate almost every scenario. Check the scenarios as shown below:

lognormal

As you can notice from the above graphs: With changing value of sigma, the curve changes its nature. This function can generate non-monotonic natures of hazard function. This is a single scenario where weibull curve does not fit well. Hence, they both complement each other well and literally can be used for all scenarios.

 

What are the applications of Survival Analysis?

To understand the applications, let’s now take a step back and think of cases where Survival analysis can be used and based on the expected distribution fit the best possible curve.

Assignment : Before looking at the answers try to attempt the best fit distribution in each case.

 

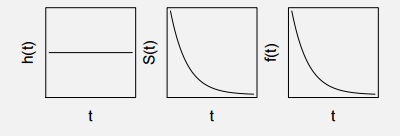
Case 1 : Time until next case of scientific innovation.

Because innovations are not biased towards any specific reasons, the hazard function is a constant line. Hence, following are the Hazard Function, Survival function and the probability distribution function:

case1

 

 

Case 2 : Life of patients of Cancer who are not responding to any treatment

Cancer gets worse with time and hence the survival rate deteriorates much faster. Following are the Hazard Function, Survival function and the probability distribution function:

case2

 

 

Case 3 : Life of a patient after surgery OR Financial state of a country/company after a big shock

Whenever there is a deteriorating effect shock. For example: Condition of patients after surgery where the risk of anything turning unfavourable, goes down with time. Below we have following type of the Hazard Function, Survival function and the probability distribution function:

case3

 

Case 4 : Life of a patient recently detected with Swine Flu or TB 

Diseases like Swine Flu or TB have a sharp impact. If the patient can survive the initial period of these diseases, the danger of death gradually subsides as the time passes on. Following are the Hazard Function, Survival function and the probability distribution function:

case4

 

The right distribution for each case:

Now let’s think over what distribution fits well in each of these cases:

Case 1 : Both Exponential and Weibull can be used for this case as hazard function is a constant curve.

Case 2 : Weibull function with gamma = 2 can be used as the hazard function is a linearly increasing curve.

Case 3 : This is kept as an assignment for this article. You won’t find a direct answer in this article but with a good basic understanding, you should have no challenge figuring this out.

Case 4 : This is the classic case of the use of Log normal distribution. The hazard function shows a peak and hence the log-normal with sigma less than 1 is suitable for this case.

 

End Notes

This article will help you understand the Survival analysis. It also explains how to estimate distributions given the survival plots. People generally miss out on understanding the application of any concept they choose to learn. In this article, we have also discussed various cases which describes the diverse applications of this Parametric Analysis. Case 3 is given as an assignment. Write your detailed answers in the box below.

Were you haunted by any questions/doubts while learning this concept? Don’t worry, ask our analytics community and never let your learning process stop by any of the hurdle which comes across your way!

Did you find the article useful? Do let us know your thoughts about this guide in the comments section below.

If you like what you just read & want to continue your analytics learning, subscribe to our emails, follow us on twitter or like our facebook page.

distribution of hazard functiondistribution of survival functionHazard functionlog normalparametric survivalsurvival analysissurvival analysis applicationssurvival plotsweibull
Tavish Srivastava
Tavish Srivastava

Tavish Srivastava, co-founder and Chief Strategy Officer of Analytics Vidhya, is an IIT Madras graduate and a passionate data-science professional with 8+ years of diverse experience in markets including the US, India and Singapore, domains including Digital Acquisitions, Customer Servicing and Customer Management, and industry including Retail Banking, Credit Cards and Insurance. He is fascinated by the idea of artificial intelligence inspired by human intelligence and enjoys every discussion, theory or even movie related to this idea.

Free Courses

Generative AI 4.7

Generative AI - A Way of Life

Explore Generative AI for beginners: create text and images, use top AI tools, learn practical skills, and ethics.
Large Language Models 4.5

Getting Started with Large Language Models

Master Large Language Models (LLMs) with this course, offering clear guidance in NLP and model training made simple.
Prompt Engineering 4.6

Building LLM Applications using Prompt Engineering

This free course guides you on building LLM apps, mastering prompt engineering, and developing chatbots with enterprise data.
LlamaIndex 4.8

Improving Real World RAG Systems: Key Challenges & Practical Solutions

Explore practical solutions, advanced retrieval strategies, and agentic RAG systems to improve context, relevance, and accuracy in AI-driven applications.
RAG systems using LlamaIndex 4.7

Microsoft Excel: Formulas & Functions

Master MS Excel for data analysis with key formulas, functions, and LookUp tools in this comprehensive course.

Recommended Articles

Responses From Readers

Clear

Write for us

Write, captivate, and earn accolades and rewards for your work
  • Reach a Global Audience
  • Get Expert Feedback
  • Build Your Brand & Audience
  • Cash In on Your Knowledge
  • Join a Thriving Community
  • Level Up Your Data Science Game
imag
Congratulations, You Did It!
Well Done on Completing Your Learning Journey. Stay curious and keep exploring!
Simple framework to build a survival analysis model on R
Simple framework to build a survival analysis model on R
Is survival analysis the right model for you?
Is survival analysis the right model for you?

We use cookies essential for this site to function well. Please click to help us improve its usefulness with additional cookies. Learn about our use of cookies in our Privacy Policy & Cookies Policy.

Show details