20 Challenging Job Interview Puzzles which every analyst should solve atleast once

Introduction

In the current scenario, getting your first break in data science can be difficult. Around 30% of analytics companies (specially the top ones) evaluate candidates on their prowess at solving puzzles. It implies that you are logical, creative and good with numbers.

The ability to bring unique perspective into solving business problems can provide you a huge advantage over other candidates. Such abilities can only be develop with regular practice and consistent efforts.

For me, solving puzzles is like mental exercise. I do it everyday and have fairly improved over period of time. To help you achieve this skill, I am sharing some of the trickiest & head scratching questions I’ve come across in my journey. These questions have been asked at companies like Goldman Sachs, Amazon, Google, JP Morgan etc.

P.S –  I want you to try solving them before checking the solution. Do share your logic & solutions in the comments. I’d love to see how uniquely can someone think!

Looking to crack your first data science interview? Puzzles are just one part of the entire process. Learn the various levels that go into cracking data science interviews with the ‘Ace Data Science Interviews‘ course, curated by experts who have conduced hundreds of these interviews!

20 Job Interview Puzzles

#1 Bag of Coins

You have 10 bags full of coins. In each bag are infinite coins. But one bag is full of forgeries, and you can’t remember which one. But you do know that a genuine coins weigh 1 gram, but forgeries weigh 1.1 grams. You have to identify that bag in minimum readings. You are provided with a digital weighing machine.

Answer: 1 reading.

Take 1 coin from the first bag, 2 coins from the second bag, 3 coins from the third bag and so on. Eventually, we’ll get 55 (1+2+3…+9+10) coins. Now, weigh all the 55 coins together. Depending on the resulting weighing machine reading, you can find which bag has the forged coins such that if the reading ends with 0.4 then it is the 4th bag, if it ends with 0.7 then it is the 7th bag and so on.

#2 Prisoners and hats

There are 100 prisoners all sentenced to death. One night before the execution, the warden gives them a chance to live if they all work on a strategy together. The execution scenario is as follows –

On the day of execution, all the prisoners will be made to stand in a straight line such that one prisoner stands just behind another and so on. All prisoners will be wearing a hat either of Blue colour or Red. The prisoners don’t know what colour of hat they are wearing. The prisoner who is standing at the last can see all the prisoners in front of him (and what colour of hat they are wearing). A prisoner can see all the hats in front of him. The prisoner who is standing in the front of the line cannot see anything.

The executioner will ask each prisoner what colour of hat they are wearing one by one, starting from the last in the line. The prisoner can only speak “Red” or “Blue”. He cannot say anything else. If he gets it right, he lives otherwise he is shot instantly. All the prisoners standing in front of him can hear the answers and gunshots.

Assuming that the prisoners are intelligent and would stick to the plan, what strategy would the prisoners make over the night to minimize the number of deaths?

Answer:

The strategy is that the last person will say ‘red’ if the number of red hats in front of him are odd and ‘blue’ if the number of red hats in front of him are even. Now, the 99th guy will see the if the red hats in front of him are odd or even. If it is odd then obviously the hat above him is blue, else it is red. From now on, it’s pretty intuitive.

#3 Blind games

You are in a dark room where a table is kept. There are 50 coins placed on the table, out of which 10 coins are showing tails and 40 coins are showing heads. The task is to divide this set of 50 coins into 2 groups (not necessarily same size) such that both groups have same number of coins showing the tails.

Answer:

Divide the group into two groups of 40 coins and 10 coins. Flip all coins of the group with 10 coins.

#4 Sand timers

You have two sand timers, which can show 4 minutes and 7 minutes respectively. Use both the sand timers(at a time or one after other or any other combination) and measure a time of 9 minutes.

Answer:

1. Start the 7 minute sand timer and the 4 minute sand timer.
2. Once the 4 minute sand timer ends turn it upside down instantly.
3. Once the 7 minute sand timer ends turn it upside down instantly.
4. After the 4 minute sand timer ends turn the 7 minute sand timer upside down(it has now minute of sand in it)

So effectively 8 + 1 = 9.

#5  Chaos in the bus

There is a bus with 100 labeled seats (labeled from 1 to 100). There are 100 persons standing in a queue. Persons are also labelled from 1 to 100.

People board on the bus in sequence from 1 to n. The rule is, if person ‘i’ boards the bus, he checks if seat ‘i’ is empty. If it is empty, he sits there, else he randomly picks an empty seat and sit there. Given that 1st person picks seat randomly, find the probability that 100th person sits on his place i.e. 100th seat.

Answer:

The final answer is the probability that the last person ends in up in his proper seat is exactly 1/2

The reasoning goes as follows:

First, observe that the fate of the last person is determined the moment either the first or the last seat is selected! This is because the last person will either get the first seat or the last seat. Any other seat will necessarily be taken by the time the last guy gets to ‘choose’.

Since at each choice step, the first or last is equally probable to be taken, the last person will get either the first or last with equal probability: 1/2.

#6 Mad men in a circle

N persons are standing in a circle. They are labelled from 1 to N in clockwise order. Every one of them is holding a gun and can shoot a person on his left. Starting from person 1, they starts shooting in order e.g for N=100, person 1 shoots person 2, then person 3 shoots person 4, then person 5 shoots person 6……..then person 99 shoots person 100, then person 1 shoots person 3, then person 5 shoots person 7……and it continues till all are dead except one. What’s the index of that last person ?

Answer:

Write 100 in binary, which is 1100100 and take the complement which is 11011 and it is 27. Subtract the complement from the original number. So 100 – 27 = 73.

Try it out for 50 people. 50 = 110010 in binary.

Complement is 1101 = 13. Therefore, 50 – 13 = 37.

For the number in form 2^n, it will be the first person. Let’s take an example:

64 = 1000000

Complement = 111111 = 63.

64-63 = 1.

You can apply this for any ’n’.

#7 Lazy people need to be smart

Four glasses are placed on the corners of a square Lazy Susan (a square plate which can rotate about it’s center). Some of the glasses are upright (up) and some upside-down (down).

A blindfolded person is seated next to the Lazy Susan and is required to re-arrange the glasses so that they are all up or all down, either arrangement being acceptable (which will be signalled by say ringing of a bell).

The glasses may be rearranged in turns with subject to the following rules: Any two glasses may be inspected in one turn and after feeling their orientation the person may reverse the orientation of either, neither or both glasses. After each turn the Lazy Susan is rotated through a random angle.

The puzzle is to devise an algorithm which allows the blindfolded person to ensure that all glasses have the same orientation (either up or down) in a finite number of turns. (The algorithm must be deterministic, i.e. non-probabilistic )

Answer:

This algorithm guarantees that the bell will ring in at most five turns:

1. On the first turn, choose a diagonally opposite pair of glasses and turn both glasses up.
2. On the second turn, choose two adjacent glasses at least one will be up as a result of the previous step. If the other is down, turn it up as well. If the bell does not ring, then there are now three glasses up and one down.
3. On the third turn, choose a diagonally opposite pair of glasses. If one is down, turn it up and the bell will ring. If both are up, turn one down. There are now two glasses down, and they must be adjacent.
4. On the fourth turn, choose two adjacent glasses and reverse both. If both were in the same orientation then the bell will ring. Otherwise there are now two glasses down and they must be diagonally opposite.
5. On the fifth turn, choose a diagonally opposite pair of glasses and reverse both. The bell will ring.

#8 These kids deserve medals

There are 10 incredibly smart boys at school: A, B, C, D, E, F, G, H, I and Sam. They run into class laughing at 8:58 am, just two minutes before the playtime ends and are stopped by a stern looking teacher: Mr Rabbit.

Mr Rabbit sees that A, B, C and D have mud on their faces. He, being a teacher who thinks that his viewpoint is always correct and acts only to enforce rules rather than thinking about the world that should be, lashes out at the poor kids.

“Silence!”, he shouts. “Nobody will talk. All of you who have mud on your faces, get out of the class!”. The kids look at each other. Each kid could see whether the other kids had mud on their faces, but could not see his own face. Nobody goes out of the class.

“I said, all of you who have mud on your faces, get out of the class!”

Still nobody leaves. After trying 5 more times, the bell rings at 9 and Mr Rabbit exasperatedly yells: “I can clearly see that at least one of you kids has mud on his face!”.

The kids grin, knowing that their ordeal will be over soon. Sure enough, after a few more times bawling of “All of you who have mud on your faces, get out of the class!”, A, B, C and D walk out of the class.

Explain how A, B, C and D knew that they had mud on their faces. What made the kids grin? Everybody knew that there was at least one kid with mud on his face. Support with a logical statement that a kid did not know before Mr Rabbit’s exasperated yell at 9, but that the kid knew right after it.

Answer:

After Mr Rabbit’s first shout, they understood that at least one boy has mud on his face. So, if it was exactly one boy, then the boy would know that he had mud on his face and go out after one shouting.

Since nobody went out after one shouting, they understood that at least two boys have mud on their faces. If it were exactly two boys, those boys would know (they would see only one other’s muddy face and they’d understand their face is muddy too) and go out after the next shouting.

Since nobody went out after the second shouting, it means there are atleast three muddy faces And so on, after the fourth shouting, A, B, C and D would go out of the class.

This explanation does leave some questions open. Everybody knew at least three others had mud on their faces, why did they have to wait for Mr. Rabbit’s shout at the first place? Why did they have to go through the all four shoutings after that as well?

In multi-agent reasoning, an important concept arises of common knowledge. Everybody knows that there are at least three muddy faces but they cannot act together on that information without knowing that everybody else knows that too. And that everybody knows that everybody knows that and so on. This is what we’ll be analyzing. It requires some imagination, so be prepared.

A knows that B, C and D have mud on their faces. A does not know if B knows that three people have mud on their faces. A knows that B knows that two people have mud on their faces. But A can’t expect people to act on that information because A does not know if B knows that C knows that there are two people with mud on their faces. If you think this is all uselessly complicated, consider this:

A can imagine a world in which he does not have mud on his face. (Call this world A) In A’s world, A can imagine B having a world where both A and B do not have mud on their faces. (Call this world AB)

A can imagine a world where B imagines that C imagines that D imagines that nobody has mud on their faces. (Call this world ABCD). So when Mr Rabbit shouted initially, it could have been that nobody was going out because a world ABCD was possible in which nobody should be going out anyway.

So here’s a statement that changes after Mr. Rabbit’s yell. World ABCD is not possible i.e. A cannot imagine a world where B imagines that C imagines that D imagines that nobody has mud on their faces. So now in world ABC, D knows he has mud on his face. And in world ABD, C knows he has mud on his face and so on.

#9 More prisoners and more hats

There are 7 prisoners sitting in a circle. The warden has caps of 7 different colours (an infinite supply of each colour). The warden places a cap on each prisoner’s head – he can chose to place any cap on any other’s head. Each prisoner can see all caps but her/his own. The warden orders everybody to shout out the colour of their respective caps simultaneously. If any one is able to guess her/his colour correctly, he sets them free. Otherwise, he send them in a dungeon to rot and die. Is it possible to devise a scheme to guarantee that nobody dies?

Answer:

Assign to each of the 7 colours a unique number from 0-6. Henceforth, we will only be doing modular arithmetic (modulo 7).

Assign to each of the 7 prisoners a unique number from 0-6. If the number assigned to prisoner P is N, then P always guesses that the sum of the colours assigned to all prisoners is M (modulo 7). Thus, he calculates his own colour under this assumption (= (M - sum(colours of the 6 prisoners he can see))%7).

There will always be a prisoner who guesses the correct sum (as the sum lies in 0-6), and this prisoner therefore correctly guesses his own colour.

If there is a solution, then exactly one prisoner is correct (no more). This is because there are 7^7 scenarios.

Each prisoner’s response is a function of the colours of the other 6, so if you fix their colours and vary his colour, you can see that he will be correct in exactly one-seventh of the cases (=7^6). The sum (across all scenarios) of the number of prisoners who are correct is 7*(7^6)=7^7.

If each scenario is to have at least one person right, this implies that each scenario cannot have more than one person who is right.

Being right about one’s colour is equivalent to being right about the sum of colours of all prisoners (modulo 7). (The colours of the other 6 are known.) So guessing one’s colour is the same as guessing the sum. How do we make sure that at least one person guesses the correct sum? By making sure that everybody guesses a different sum.

#10 All men must die

One day, an alien comes to Earth. Every day, each alien does one of four things, each with equal probability to:

(i) Kill himself
(ii) Do nothing
(iii) Split himself into two aliens (while killing himself)
(iv) split himself into three aliens (while killing himself)

What is the probability that the alien species eventually dies out entirely?

Answer:

The answer is √2 – 1.

Suppose that the probability of aliens eventually dying out is x.

Then for n aliens, the probability of eventually dying out is xⁿ because we consider every alien as a separate colony. Now, if we compare aliens before and after the first day, we get:

x = (1 /4) * 1 + (1 /4) * x + (1 /4) * x² + (1 /4) * x³

x³ + x² − 3x + 1 = 0

(x − 1)(x 2 + 2x − 1) = 0

We get,  x = 1, −1 − √ 2, or − 1 + √ 2

We claim that x cannot be 1, which would mean that all aliens eventually die out. The number of aliens in the colony is, on average, multiplied by 0+1+2+3 4 = 1.5 every minute, which means in general the aliens do not die out. (A more rigorous line of reasoning is included below.) Because x is not negative, the only valid solution is x = √ 2 − 1.

To show that x cannot be 1, we show that it is at most √ 2−1.

Let xⁿ be the probability that a colony of one bacteria will die out after at most n minutes. Then, we get the relation:

xn + 1 = 1/4 (1 + xn + x²n + x²n)

We claim that x_n ≤ √ 2 − 1 for all n, which we will prove using induction.

It is clear that x₁ = 1 /4 ≤ √ 2 − 1. Now, assume x_k ≤ √ 2 − 1 for some k. We have:

xk+1 ≤ 1/4 (1 + xk + x²k + x³k )

≤ 1/4 ( 1 + (√ 2 − 1) + (√ 2 − 1)² + (√ 2 − 1)³ )

= √ 2 − 1

which completes the proof that x_n ≤ √ 2 − 1 for all n. Now, we note that as n becomes large, x_n approaches x. Using formal notation, this is:

x = lim (n →∞) xn ≤ √ 2 − 1, so x cannot be 1.

#11 Lumos

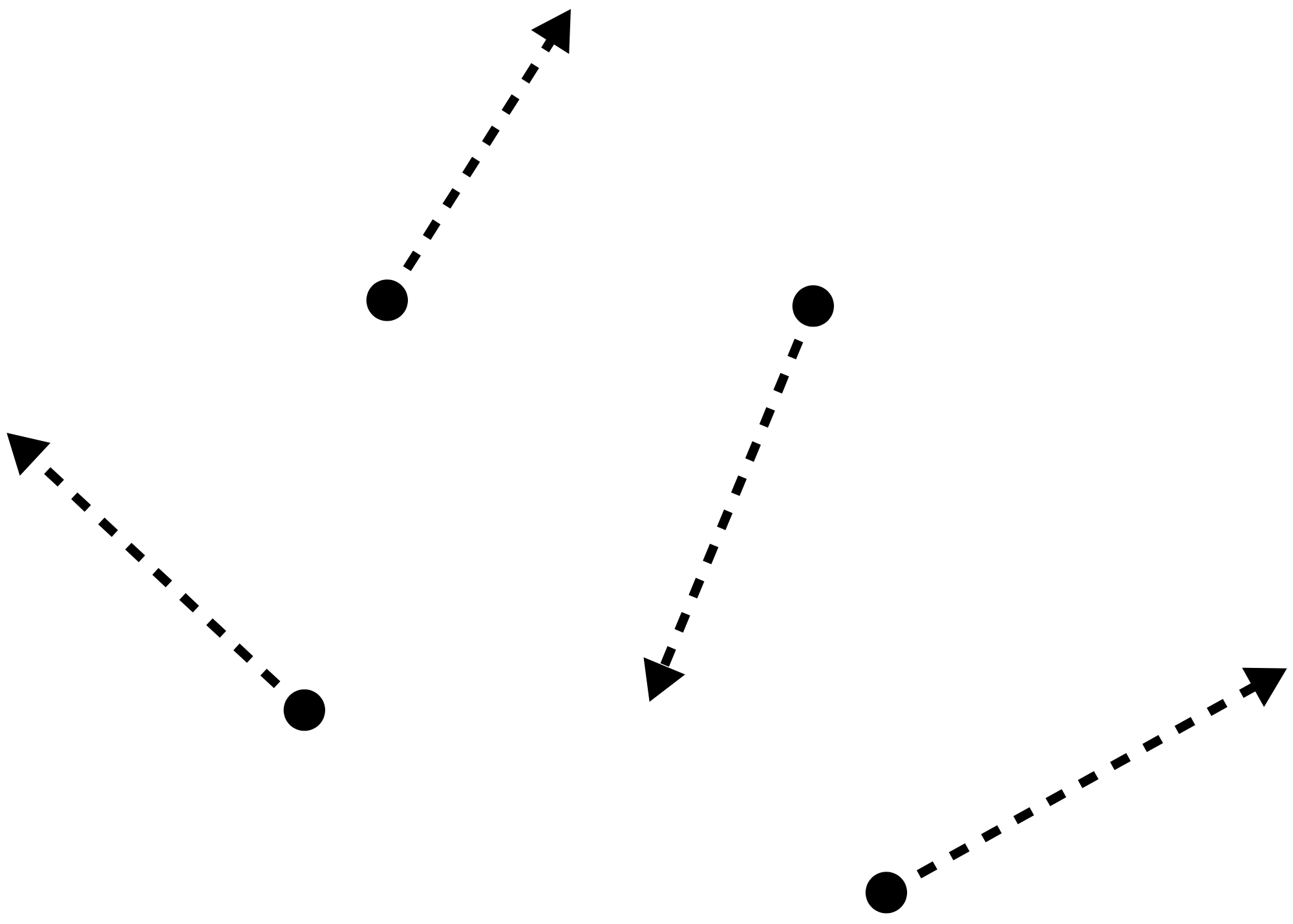
A photon starts moving in random direction from the center of square of size 3. Let’s say it first colloids to the glass wall AB. What is the expected distance traveled by photon before hitting the wall AB again?

Answer:

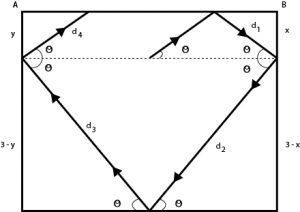
Above is a pictorial representation of the photon. We can calculate it’s distance as shown below:

d1 = x cosec (Θ)

d2 = (3 - x) cosec (Θ)

d3 = (3 - y) cosec (Θ)

d4 = y cosec (Θ)

Total distance = d1+ d2 + d3 + d4

= 6 cosec (Θ)

We know, Θ varies between Π/4 and 3Π/4

Therefore, E(distance) = 6 E (cosec Θ)
= 6 x (2 /Π) ∫cosec(Θ)dΘ    (limits Π/4 to 3Π/4)
= 12/Π ln (√2 + 1/√2 + 1)

#12 4 points in a sphere

Consider a unit sphere. 4 points are randomly chosen on it, what is the probability that the centre (of sphere) lies within the tetrahedron (/ polygon) formed by those 4 points?

Answer:

Let A, B and C be random points on the sphere with Aa, Bb and Cc being diameters.

The spherical (minor) triangle abc is common to the hemispheres abc, bca and cab (where the notation abc represents the hemisphere cut off by the great circle through a and b and containing the point c, etc), therefore the probability that a further random point, D, lies on this triangle is:

1/2 x 1/2 x 1/2 = 1/8

(For centre to lie in the tetrahedron D should lie in the triangle i.e the opposite hemisphere of ABC)

#13 Misogynist country

In a country in which people only want boys, every family continues to have children until they have a boy. If they have a girl, they have another child. If they have a boy, they stop. What is the proportion of boys to girls in the country?

Answer:

Following is the required calculation:

Expected Number of boys for 1 family = 1*(Probability of 1 boy) + 1*(Probability of 1 girl and a boy) + 1*(Probability of 2 girls and a boy) + …

For C couples = 1*(C*1/2) + 1*(C*1/2*1/2) + 1*(C*1/2*1/2*1/2) + …

Expected Number of boys = C/2 + C/4 + C/8 + C/16 + …

Expected Number of boys = C

Expected Number of girls for 1 family = 0*(Probability of 0 girls) + 1*(Probability of 1 girl and a boy) + 2*(Probability of 2 girls and a boy) + …

For C couples  = 0*(C*1/2) + 1*(C*1/2*1/2) + 2*(C*1/2*1/2*1/2) + …

Expected Number of girls = 0 + C/4 + 2*C/8 + 3*C/16 + …

Expected Number of girls = C

Therefore, the proportion is C/C = 1:1

#14 The Red wedding

A bad king has a cellar of 1000 bottles of delightful and very expensive wine. A neighbour queen plots to kill the bad king and sends a servant to poison the wine.

Fortunately (or say unfortunately) the bad king’s guards catch the servant after he could poison only one bottle. Alas, the guards don’t know which bottle, but know that the poison is so strong that even if diluted 100,000 times it would still kill the king.

Furthermore, it takes one month to have an effect. The bad king decides he will get some of the prisoners in his vast dungeons to drink the wine. Being a clever bad king, he knows that he needs to murder no more than 10 prisoners – believing he can fob off such a low death rate – and will still be able to drink the rest of the wine (999 bottles) at his wedding party in 5 weeks time.

Explain what is in mind of the king, how will he be able to do so ? (he has only 10 prisoners in his prisons)

Answer:

The number the bottles are 1 to 1000. Now, write the number in binary format. We can write it as:

bottle 1 = 0000000001 (10 digit binary)

bottle 2 = 0000000010

.

.

.

bottle 500 = 0111110100

bottle 1000 = 1111101000

Now, take 10 prisoners and number them 1 to 10. Let prisoner 1 take a sip from every bottle that has a 1 in its least significant bit. And, this process will continue for every prisoner until the last prisoner is reached. For example:

Prisoner = 10 9 8 7 6 5 4 3 2 1

Bottle 924 = 1 1 1 0 0 1 1 1 0 0

For instance, bottle no. 924 would be sipped by 10,9,8,5,4 and 3. That way if bottle no. 924 was the poisoned one, only those prisoners would die.

After four weeks, line the prisoners up in their bit order and read each living prisoner as a 0 bit and each dead prisoner as a 1 bit. The number that you get is the bottle of wine that was poisoned. We know, 1000 is less than 1024 (2^10). Therefore, if there were 1024 or more bottles of wine it would take more than 10 prisoners.

#15 Life and luck

You and your friend are caught by gangsters and made to play a game to determine if you should live or die. The game is simple.

There is a deck of cards and you both have to choose a card. You can look at each other’s cards but not at the card you have chosen. You both will survive if both are correct in guessing the card they have chosen. Otherwise both die.

What is the probability of you surviving if you and your friend play the game optimally?

Answer:

We know, A and B have picked a card at random from a deck. A can see B’s card and vice versa. So, A knows (s)he has not picked B’s card, but apart from that, (s)he knows that the card is equally probable to be any of the other 51 cards. So, if A guesses B’s card, they lose. But if A guesses any other card, there’s a 1/51 chance that A is right. This also implies that total probability of success <= 1/51.

A’s aim now is to tell any card apart from B’s card that gives B the most information about B’s own card. So they can plan beforehand as follows:

Consider the sequence of cards Clubs 1-13, Diamonds 1-13, Hearts 1-13, Spades 1-13. A will tell the card after B’s card in this sequence. (If A says 4 of Hearts, it means B has 3 of Hearts. If A says Ace of Clubs, it means B has King of Spades)

With A’s guess, which is always different from B’s card, B gets to know exactly which card (s)he has and can always guess correctly. So the probability of success is 1/51, which is the maximum achievable.

#16 Weighing balls

You have 12 balls that all weigh the same except one, which is either slightly lighter or slightly heavier. The only tool you have is a balance scale that can only tell you which side is heavier. Using only three weightings, how can you deduce, without a shadow of a doubt, which is the odd one out, and if it is heavier or lighter than the others?

Answer:

First we weigh {1,2,3,4} on the left and {5,6,7,8} on the right. There are three scenarios which can arise from this:

If they balance, then we know 9, 10, 11 or 12 is fake. Weigh {8, 9} and {10, 11} (Note: 8 is surely not fake). If they balance, we know 12 is the fake one. Just weigh it with any other ball and figure out if it is lighter or heavier.

If {8, 9} is heavier, then either 9 is heavy or 10 is light or 11 is light. Weigh {10} and {11}. If they balance, 9 is fake (heavier). If they don’t balance then whichever one is lighter is fake (lighter).

If {8, 9} is lighter, then either 9 is light or 10 is heavy or 11 is heavy. Weigh {10} and {11}. If they balance, 9 is fake (lighter). If they don’t balance then whichever one is heavier is fake (heavier).

If {1,2,3,4} is heavier, we know either one of {1,2,3,4} heavier or one of {5,6,7,8} is lighter but it is guarantees that {9,10,11,12} are not fake. This is where it gets really tricky, watch carefully. Weigh {1,2,5} and {3,6,9} (Note: 9 is surely not fake).

If they balance, then either 4 is heavy or 7 is light or 8 is light. Following the last step from the previous case, we weigh {7} and {8}. If they balance, 4 is fake(heavier). If they don’t balance then whichever one is lighter is fake (lighter).

If {1,2,5} is heavier, then either 1 is heavy or 2 is heavy or 6 is light. Weigh {1} and {2}. If they balance, 6 is fake (lighter). If they don’t balance then whichever one is heavier is fake (heavier).

If {3,6,9} is heavier, then either 3 is heavy or 5 is light. Weigh {5} and {9}. They won’t balance. If {5} is lighter, 5 is fake (lighter). If they balance, 3 is fake (heavier).

If {5,6,7,8} is heavier, it is the same situation as if {1,2,3,4} was heavier. Just perform the same steps using 5,6,7 and 8. Unless maybe you are too lazy to try and reprocess the steps, then you continue reading the solution. Weigh {5,6,1} and {7,2,9} (Note: 9 is surely not fake).

If they balance, then either 8 is heavy or 3 is light or 4 is light. Following the last step from the previous case, we weigh {3} and {4}. If they balance, 8 is fake(heavier). If they don’t balance then whichever one is lighter is fake (lighter).

If {5,6,1} is heavier, then either 5 is heavy or 6 is heavy or 2 is light. Weigh {5} and {6}. If they balance, 2 is fake (lighter). If they don’t balance then whichever one is heavier is fake (heavier).

If {7,2,9} is heavier, then either 7 is heavy or 1 is light. Weigh {1} and {9}. If they balance, 7 is fake (heavier). If they don’t balance then 1 is fake (lighter).

#17 Bias and unbias

Robin and Williams are playing a game. An unbiased coin is tossed repeatedly. Robin wins as soon as the sequence of tosses HHT appears. Williams wins as soon as the sequence of tosses HTH appears. The game ends when one of them wins. What are the probabilities of winning for each player?

Answer: (Robin) HHT – 2/3  (Williams) HTH – 1/3

Let the probability of Robin winning be p. The probability of Williams winning is (1-p). If the first toss is tails, it is as good as the game has not started, hence the probability of Robin winning is p after the first tail.

p = (1/2)*p + ….

Let the first toss be heads. If the second toss is heads, then Robin definitely wins. Since HH has occurred, and at some point, tails will occur, so HHT will occur. Hence Robin wins with probability 1 for HH.

p = (1/2 )*p + (1/2)*((1/2)*1 + .....)

Let the second toss be tails. If the third toss is heads, Robin loses as HTH occurs. If the third toss is tails (HTT) – since two tails have occurred in a row, now it is as good as the game has started from the beginning, so the chances of Robin winning are back to p.

         T            HH         HTH   HTT

p = (1/2)*p + 1/2 ((1/2)*1 + 1/2 ((1/2)*0 + (1/2) * p))

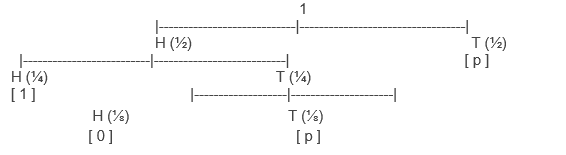
p = (1/2)*p + (1/4)*1 + (1/8)*0 + (1/8)*p

Finally, solving this equation gives us p = 2/3.

#18 Chameleons go on a date

On an island live 13 purple, 15 yellow and 17 maroon chameleons. When two chameleons of different colors meet, they both change into the third color. Is there a sequence of pairwise meetings after which all chameleons have the same color?

Answer:

Let <p, y, m> denote a population of p purple, y yellow and m maroon chameleons. Can population <13, 15, 17> be transformed into <45, 0, 0> or <0, 45, 0> or <0, 0, 45> through a series of pairwise meetings?

We can define function:

X(p, y, m) = (0p + 1y + 2m) mod 3

An interesting property of X is that its value does not change after any pairwise meeting because

X(p, y, m) = X(p-1, y-1, m+2) = X(p-1, y+2, m-1) = X(p+2, y-1, m-1)

Now X(13, 15, 17) equals 1. However,

X(45, 0, 0) = X(0, 45, 0) = X(0, 0, 45) = 0**

This means that there is no sequence of pairwise meetings after which all chameleons will have identical colour.

#19 The Einstein puzzle

Answer the question using the given information and hints.

1. In a street there are five houses, painted five different colors.
2. In each house lives a person of different nationality
3. These five homeowners each drink a different kind of beverage, smoke different brand of cigar and keep a different pet.

The Question: Who owns the fish ?

Hints:

1. The British man lives in a red house.
2. The Swedish man keeps dogs as pets.
3. The Danish man drinks tea.
4. The Green house is next to, and on the left of the White house.
5. The owner of the Green house drinks coffee.
6. The person who smokes Pall Mall rears birds.
7. The owner of the Yellow house smokes Dunhill.
8. The man living in the center house drinks milk.
9. The Norwegian lives in the first house.
10. The man who smokes Blends lives next to the one who keeps cats.
11. The man who keeps horses lives next to the man who smokes Dunhill.
12. The man who smokes Blue Master drinks beer.
13. The German smokes Prince.
14. The Norwegian lives next to the blue house.
15. The Blends smoker lives next to the one who drinks water.

FYI – This question is famously known as Einstein Puzzle.

Answer: Read More

#20 Circles whirl my mind

Consider natural numbers form 1 to 21 that is 1,2,3,4….21. Find number of distinct circular permutation of these numbers such that any number must have different neighbours.

Answer – Still thinking.! Post solution if you get.

End Notes

I hope these questions would have ‘dared’ you enough to get your brain rolling. I understand these question might appear as challenging to a lot of you, but believe me, they aren’t difficult. If you find any trouble in understanding any solution or question, feel free to drop me a message below.

I’ve obtained the solution from various sources. Also, I’ve answered some on my own. Try to understand these questions well. Once you do it, you’d find it easier to solve similar questions during interviews.

Did you like solving these puzzles? Do let me know your experience, suggestions & solutions in the comments below. I am excited to see if you can think any different!

I also encourage you to check out the ‘Ace Data Science Interviews‘ course to learn how to solve such puzzles and many other important aspects of the interview rounds!

You can test your skills and knowledge. Check out Live Competitions and compete with best Data Scientists from all over the world.