45 questions to test a Data Scientist on Regression (Skill test – Regression Solution)

Solution: A

Choosing the right degree of polynomial plays a critical role in fit of regression. If we choose higher degree of polynomial, chances of overfit increase significantly.

Solution: D

We need to calculate the residuals for each cross validation point. After fitting the line with 2 points and leaving 1 point for cross validation.

Leave one out cross validation mean square error = (2^2 +(2/3)^2 +1^2) /3 = 49/27

1. MLE may not always exist
2. MLE always exists
3. If MLE exist, it (they) may not be unique
4. If MLE exist, it (they) must be unique

A. 1 and 4

B. 2 and 3

C. 1 and 3

D. 2 and 4

A. You will always have test error zeroB. You can not have test error zero

C. None of the above

A. If R Squared increases, this variable is significant.

B. If R Squared decreases, this variable is not significant.

C. Individually R squared cannot tell about variable importance. We can’t say anything about it right now.

D. None of these.

A. Mean of residuals is always zero

B. Mean of residuals is always less than zero

C. Mean of residuals is always greater than zero

D. There is no such rule for residuals.

Solution: A

Sum of residual in regression is always zero. It the sum of residuals is zero, the ‘Mean’ will also be zero.

A. Linear Regression with varying error termsB. Linear Regression with constant error terms

C. Linear Regression with zero error terms

D. None of these

Solution: A

The presence of non-constant variance in the error terms results in heteroskedasticity. Generally, non-constant variance arises because of presence of outliers or extreme leverage values.

You can refer this article for more detail about regression analysis.

A. Correlation coefficient = 0.9B. The p-value for the null hypothesis Beta coefficient =0 is 0.0001

C. The t-statistic for the null hypothesis Beta coefficient=0 is 30

D. None of these

Solution: A

Correlation between variables is 0.9. It signifies that the relationship between variables is fairly strong.

On the other hand, p-value and t-statistics merely measure how strong is the evidence that there is non zero association. Even a weak effect can be extremely significant given enough data.

1. The true relationship between dependent y and predictor x is linear
2. The model errors are statistically independent
3. The errors are normally distributed with a 0 mean and constant standard deviation
4. The predictor x is non-stochastic and is measured error-free

A. 1,2 and 3.

B. 1,3 and 4.

C. 1 and 3.

D. All of above.

Solution: D

When deriving regression parameters, we make all the four assumptions mentioned above. If any of the assumptions is violated, the model would be misleading.

A. Scatter plotB. Barchart

C. Histograms

D. None of these

Solution: A

To test the linear relationship between continuous variables Scatter plot is a good option. We can find out how one variable is changing w.r.t. another variable. A scatter plot displays the relationship between two quantitative variables.

1. Linear Regression
2. Logistic Regression

A. 1 and 2

B. only 1

C. only 2

D. None of these.

Solution: B

Logistic Regression is used for classification problems. Regression term is misleading here.

A. The age is good predictor of healthB. The age is poor predictor of health

C. None of these

Solution: C

Correlation coefficient range is between [-1 ,1]. So -1.09 is not possible.

A. Vertical offset

B. Perpendicular offset

C. Both but depend on situation

D. None of above

Solution: A

We always consider residual as vertical offsets. Perpendicular offset are useful in case of PCA.

1. Simple Linear regression will have high bias and low variance
2. Simple Linear regression will have low bias and high variance
3. polynomial of degree 3 will have low bias and high variance
4. Polynomial of degree 3 will have low bias and Low variance

A. Only 1

B. 1 and 3

C. 1 and 4

D. 2 and 4

Solution: C

If we fit higher degree polynomial greater than 3, it will overfit the data because model will become more complex. If we fit the lower degree polynomial less than 3 which means that we have less complex model so in this case high bias and low variance. But in case of degree 3 polynomial it will have low bias and low variance.

1. Overfitting is more likely if we have less data
2. Overfitting is more likely when the hypothesis space is small

Which of the above statement(s) are correct?

A. Both are False

B. 1 is False and 2 is True

C. 1 is True and 2 is False

D. Both are True

Solution: C

1.With small training dataset, it’s easier to find a hypothesis to fit the training data exactly i.e. overfitting.

2. We can see this from the bias-variance trade-off. When hypothesis space is small, it has higher bias and lower variance. So with a small hypothesis space, it’s less likely to find a hypothesis to fit the data exactly i.e. underfitting.

A. It is more likely for X1 to be excluded from the modelB. It is more likely for X1 to be included in the model

C. Can’t say

D. None of these

Solution: B

Big feature values =⇒ smaller coefficients =⇒ less lasso penalty =⇒ more likely to have be kept

A. Ridge regression uses subset selection of featuresB. Lasso regression uses subset selection of features

C. Both use subset selection of features

D. None of above

Solution: B

“Ridge regression” will use all predictors in final model whereas “Lasso regression” can be used for feature selection because coefficient values can be zero. For more detail click here.

1. R-Squared and Adjusted R-squared both increase

1. R-Squared increases and Adjusted R-squared decreases

1. R-Squared decreases and Adjusted R-squared decreases

1. R-Squared decreases and Adjusted R-squared increases

A. 1 and 2

B. 1 and 3

C. 2 and 4

D. None of the above

Solution: A

Each time when you add a feature, R squared always either increase or stays constant, but it is not true in case of Adjusted R squared. If it increases, the feature would be significant.

1. The training error in first model is higher when compared to second and third model.
2. The best model for this regression problem is the last (third) model, because it has minimum training error.
3. The second model is more robust than first and third because it will perform better on unseen data.
4. The third model is overfitting data as compared to first and second model.
5. All models will perform same because we have not seen the test data.

A. 1 and 3

B. 1 and 3

C. 1, 3 and 4

D. Only 5

Solution: C

The trend of the data looks like a quadratic trend over independent variable X. A higher degree (Right graph) polynomial might have a very high accuracy on the train population but is expected to fail badly on test dataset. But if you see in left graph we will have training error maximum because it under-fits the training data.

1. R Squared

1. Adjusted R Squared

1. F Statistics

1. RMSE / MSE / MAE

A. 2 and 4.

B. 1 and 2.

C.  2, 3 and 4.

D. All of the above.

Solution: D

These (R Squared, Adjusted R Squared, F Statistics , RMSE / MSE / MAE ) are some metrics which you can use to evaluate your regression model.

1. We don’t have to choose the learning rate
2. It becomes slow when number of features is very large
3. No need to iterate

A. 1 and 2

B. 1 and 3.

C. 2 and 3.

D. 1,2 and 3.

Solution: D

Instead of gradient descent, Normal Equation can also be used to find coefficients. Refer this article for read more about normal equation.

Y = β0 +  β1 X1 + β2 X2……+ βn Xn

Which of the following statement(s) are true?

1. If Xi changes by an amount ∆Xi, holding other variables constant, then the expected value of Y changes by a proportional amount βi ∆Xi, for some constant βi (which in general could be a positive or negative number).
2. The value of βi is always the same, regardless of values of the other X’s.
3. The total effect of the X’s on the expected value of Y is the sum of their separate effects.

Note: Features are independent of each others(zero interaction).

A. 1 and 2

B. 1 and 3

C. 2 and 3

D. 1,2 and 3

Solution: D

1. The expected value of Y is a linear function of the X variables. This means:
   1. If X i changes by an amount ∆X i , holding other variables fixed, then the expected value of Y changes by a proportional amount β i ∆X i , for some constant β i (which in general could be a positive or negative number).
   2. The value of β i is always the same, regardless of values of the other X’s.
   3. The total effect of the X’s on the expected value of Y is the sum of their separate effects.

1. The unexplained variations of Y are independent random variables (in particular, not “auto correlated” if the variables are time series)
2. They all have the same variance (“homoscedasticity”).
3. They are normally distributed.

A. 1B. 2

C. Can’t Say

Solution: B

In simple linear regression, there is one independent variable so 2 coefficients (Y=a+bx).

Note:

1. Scale is same in both graphs for both axis.
2. X axis is independent variable and Y-axis is dependent variable.

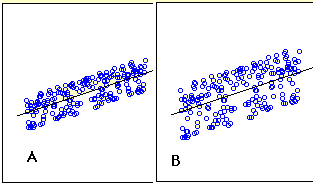
Which of the following statement is true about sum of residuals of A and B?

A) A has higher than B

B) A has lower than B

C) Both have same

D) None of these

Solution: C

Sum of residuals always zero.

A. Yes
B. No

Solution: B

It is not necessary. They could have non linear relationship

A. True
B. False

Solution: A

Note: Consider remaining parameters are same.

1. Training accuracy always decreases.
2. Training accuracy always increases or remain same.
3. Testing accuracy always decreases
4. Testing accuracy always increases or remain same

A. Only 2

B. Only 1

C. Only 3

D. Only 4

Solution: A

Adding more features to model will always increase the training accuracy i.e. low bias. But testing accuracy increases if feature is found to be significant.

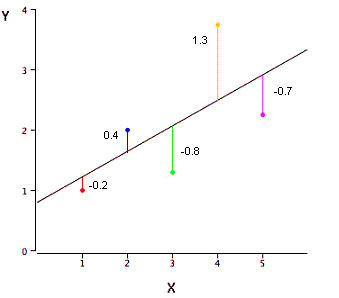
A. 3.02

B. 0.75

C. 1.01

D. None of these

Solution: A

SSE is the sum of the squared errors of prediction, so SSE = (-.2)^2 + (.4)^2 + (-.8)^2 + (1.3)^2 + (-.7)^2 = 3.02

A. Plot2

B. Plot1

C. Both

D. Can’t say

Solution: A

Plot 2 is definitely a better representation of the association between height and weight. As individuals get taller, they take up more volume, which leads to an increase in height, so a positive relationship is expected. The plot on the right has this positive relationship while the plot on the left shows a negative relationship.

A. Yes

B. No

C. More information is required

D. None of these.

Solution: C

A. The relationship is symmetric between x and y in both.

B. The relationship is not symmetric between x and y in both.

C. The relationship is not symmetric between x and y in case of correlation but in case of regression it is symmetric.

D. The relationship is symmetric between x and y in case of correlation but in case of regression it is not symmetric.

Solution: D

1. Correlation is a statistic metric that measures the linear association between two variables. It treats y and x symmetrically.
2. Regression is setup to predict y from x. The relationship is not symmetric.

A. True
B. False

Solution: B

The skewness is not directly related to the relationship between the mean and median.

Are all the given datasets same?

A. Yes

B. No

C. Can’t Say

Solutiom: C

To answer this question, you should know about Anscombe’s quartet. Refer this link  to read more about this.

1. In case of fewer observations, it is easy to overfit the data.
2. In case of fewer observations, it is hard to overfit the data.
3. In case of more observations, it is easy to overfit the data.
4. In case of more observations, it is hard to overfit the data.

A. 1 and 4

B. 2 and 3

C. 1 and 3

D. None of theses

Solution: A

In particular, if we have very few observations and it’s small, then our models can rapidly overfits data. Because we have only a few points and as we’re increasing in our model complexity like the order of the polynomial, it becomes very easy to hit all of our observations.

On the other hand, if we have lots and lots of observations, even with really, really complex models, it is difficult to overfit because we have dense observations across our input.

A. In case of very large lambda; bias is low, variance is lowB. In case of very large lambda; bias is low, variance is high

C. In case of very large lambda; bias is high, variance is low

D. In case of very large lambda; bias is high, variance is high

Solution: C

If lambda is very large it means model is less complex. So in this case bias is high and variance in low.

A. In case of very small lambda; bias is low, variance is lowB. In case of very small lambda; bias is low, variance is high

C. In case of very small lambda; bias is high, variance is low

D. In case of very small lambda; bias is high, variance is high

Solution: B

If  lambda is very small it means model is complex. So in this case bias is low and variance is high because model will overfit the data.

1. When lambda is 0, model works like linear regression model
2. When lambda is 0, model doesn’t work like linear regression model
3. If lambda goes to infinity, we get very, very small coefficients approaching 0
4. If lambda goes to infinity, we get very, very large coefficients approaching infinity

A. 1 and 3

B. 1 and 4

C. 2 and 3

D. 2 and 4

Solution: A

Specifically, we can see that when lambda is 0, we get our least square solution. When lambda goes to infinity, we get very, very small coefficients approaching 0.

Note:

1. All residuals are standardized.
2. The plots are between predicted values Vs. residuals

A. 1

B. 2

C. 3

D. 1 and 2

Solution: C

There should not be any relationship between predicted values and residuals. If there exist any relationship between them means model has not perfectly capture the information in data.

A. Ridge regressionB. Lasso

C. Both Ridge and Lasso

D. None of both

Solution: B

The Lasso does not admit a closed-form solution. The L1-penalty makes the solution non-linear. So we need to approximate the solution.

If you want to read more about closed form solutions, refer this link.

Which bold point, if removed will have the largest effect on fitted regression line as shown in above figure(dashed)?

A) a

B) b

C) c

D) d

Solution: D

Linear regression is sensitive to outliers in the data. Although c is also an outlier in given data space but it is closed to the regression line(residual is less) so it will not affect much.

A: By 1B. No change

C. By intercept

D. By its Slope

Solution: D

Equation for simple linear regression: Y=a+bx. Now if we increase the value of x by 1 then the value of y would be a+b(x+1) i.e. value of y will get incremented by b.

A. Sigmoid

B. Mode

C. Square

D. Probit

Solution: A

Sigmoid function is used to convert output probability between [0,1] in logistic regression.

A. Both will be differentB. Both will be same

C. Can’t say

D. None of these

Solution: B

Refer this link

A. We need to fit n model in n-class classification problem.B. We need to fit n-1 models to classify into n classes.

C. We need to fit only 1 model to classify into n classes.

D. None of these.

Solution: A

If there are n classes, then n separate logistic regression has to fit, where the probability of each category is predicted over the rest of the categories combined.

Take a example of 3-class(-1,0,1) classification. Then need to train 3 logistic regression classifiers.

1. -1 vs 0 and 1
2. 0 vs -1 and 1
3. 1 vs 0 and -1

Which of the following statement(s) is true about β0 and β1 values of two logistics models (Green, Black)?

Note: consider Y = β0 + β1*X.  Here, β0 is intercept and  β1 is  coefficient.

A. β1 for Green is greater than Black

B. β1 for Green is lower than Black

C. β1 for both models is same

D. Can’t Say.

Solution: B

β0 and β1: β0 = 0, β1 = 1 is in X1 color(black) and β0 = 0, β1 = −1 is in X4 color (green)