I came across Julia a while ago even though it was in its early stages, it was still creating ripples in the numerical computing space. Julia is a work straight out of MIT, a high-level language that has a syntax as friendly as Python and performance as competitive as C. This is not all, It provides a sophisticated compiler, distributed parallel execution, numerical accuracy, and an extensive mathematical function library.
But this article isn’t about praising Julia, it is about how can you utilize it in your workflow as a data scientist without going through hours of confusion which usually comes when we come across a new language.
Before we can start our journey into the world of Julia, we need to set up our environment with the necessary tools and libraries for data science.

Jupyter notebook has become an environment of choice for data science since it is really useful for both fast experimenting and documenting your steps. There are other environments too for Julia like Juno IDE but I recommend to stick with the notebook. Let’s look at how we can setup the same for Julia.
Go to the Julia prompt and type the following code
julia> Pkg.add(“IJulia”)
Note: Pkg.add() command downloads files and package dependencies in the background and installs it for you. For this, you should have an active internet connection. If your internet is slow, you might have to wait for some time.
After ijulia is successfully installed you can type the following code to run it,
julia> using IJulia
julia> notebook()
By default, the notebook “dashboard” opens in your home directory ( homedir() ), but you can open the dashboard in a different directory with notebook(dir=”/some/path”) .
There you have your environment all set up. Let’s install some important Julia libraries that we’d be needing for this tutorial.
A simple way of installing any package in Julia is using the command Pkg.add(“..”). Like Python or R, Julia too has a long list of packages for data science. I thought instead of installing all the packages together it would be better if we install them as and when needed, that’d give you a good sense of what each package does. So we will be following that process for this article.
Julia is a language that derives a lot of syntax from other data analysis tools like R, Python, and MATLAB. If you are from one of these backgrounds, it would take you no time to get started with it. Let’s learn some of the basic syntaxes. If you are in a hurry here’s a cheat sheet comparing syntax of all the three languages: https://cheatsheets.quantecon.org/
julia> using IJulia
julia> notebook()
There, you created your first Julia notebook! Just like you use jupyter notebook for R or Python, you can write Julia code here, train your models, make plots and so much more all while being in the familiar environment of jupyter.

Go ahead and play around a bit with the notebook to get familiar.
The following are some of the most common data structures we end up using when performing data analysis on Julia:
A vector is a 1-Dimensional array. A vector can be created by simply writing numbers separated by a comma in square brackets. If you add a semicolon, it will change the row. Vectors are widely used in linear algebra.
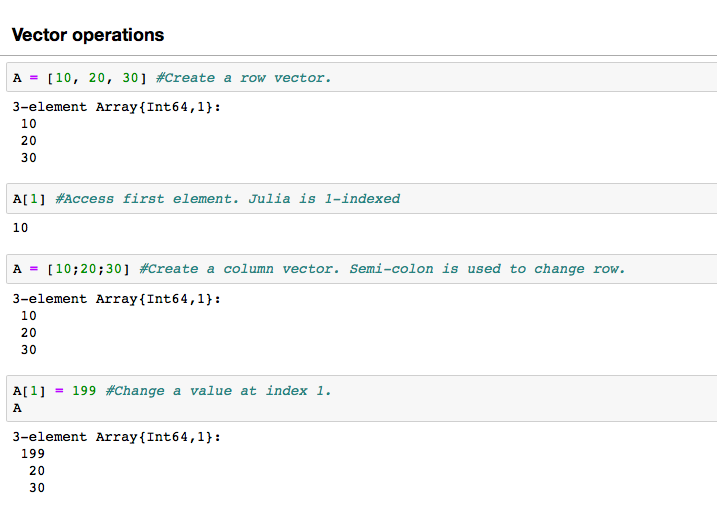
Note that in Julia the indexing starts from 1, so if you want to access the first element of an array you’ll do A[1].
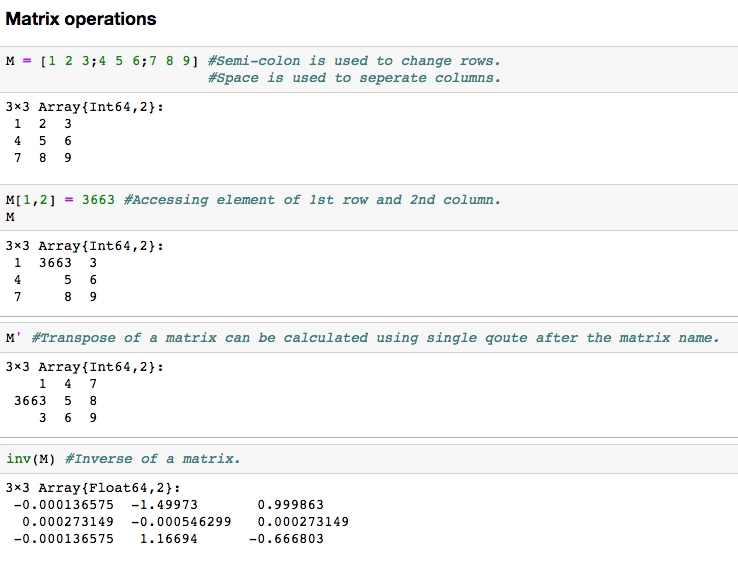
Another data structure that is widely used in linear algebra, it can be thought of as a multidimensional array. Here are some basic operations that can be performed in a matrix
It is an unordered set of key: value pairs, with the requirement that the keys are unique (within one dictionary). You can create a dictionary using the Dict() function.
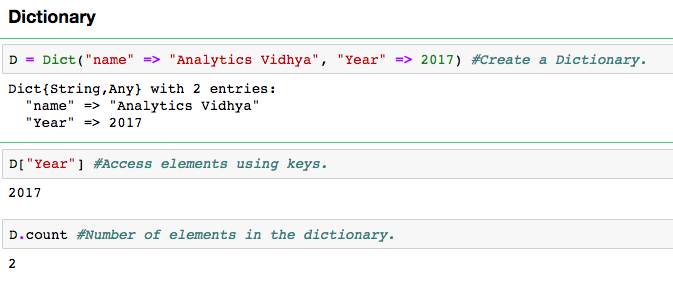
Notice that “=>” operator is used to link key with their respective values. You access the values of the dictionary using its key.
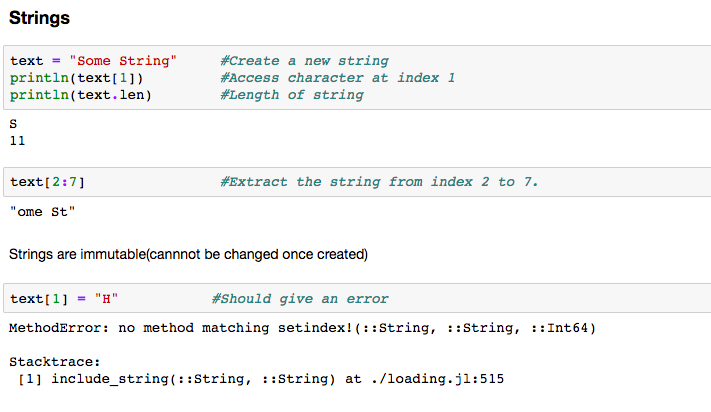
They can simply be defined by use of double ( ” ) or triple ( ”’ ) inverted commas. Like Python, strings in Julia are also immutable(they can’t be changed once created). Look at the error below.
Like most languages, Julia also has a FOR-loop which is the most widely used method for iteration. It has a simple syntax:
for i in [Julia Iterable]
expression(i)
endHere “Julia Iterable” can be a vector, string or other advanced data structures which we will explore in later sections. Let’s take a look at a simple example, determining the factorial of a number ‘n’.
fact=1
for i in range(1,5)
fact = fact*i
end
print(fact)Julia also supports the while loop and various conditionals like if, if/else, for selecting a bunch of statements over another based on the outcome of the condition. Here is an example,
if N>=0
print("N is positive")
else
print("N is negative")
endThe above code snippet performs a check on N and prints whether it is a positive or a negative number. Note that julia is not indentation sensitive like Python but it is a good practice to indent your code that’s why you’ll find code samples in this article well indented. Here is a list of Julia conditional constructs compared to their counterparts in MATLAB and Python.

You can learn more about Julia basics here .
Now that we are familiar with Julia fundamentals, let’s take a deep dive into problem-solving. Yes, I mean making a predictive model! In the process, we use some powerful libraries and also come across the next level of data structures. We will take you through the 3 key phases:
The first step in any kind of data analysis is exploring the dataset at hand. There are two ways to do that, the first is exploring the data tables and applying statistical methods to find patterns in numbers and the second is plotting the data to find patterns visually.
The former requires an advanced data structure that is capable of handling multiple operations and at the same time is fast and scalable. Like many other data analysis tools, Julia provides one such structure called DataFrame. You need to install the following package for using it:
julia> Pkg.add(“DataFrames.jl”) A dataframe is similar to Excel workbook – you have column names referring to columns and you have rows, which can be accessed with the use of row numbers. The essential difference is that column names and row numbers are known as column and row index, in case of dataframes . This is similar to pandas.DataFrame in Python or data.table in R.
Let’s work with a real problem. We are going to analyze an Analytics Vidhya Hackathon as a practice dataset.
You can download the dataset from here . Here is the description of variables:

In Julia we import a library by the following command:
using <library_name>Let’s first import our DataFrames.jl library and load the train.csv file of the data set:
using DataFrames
train = readtable(“train.csv”)Once the data set is loaded, we do preliminary exploration on it. Such as finding the size(number of rows and columns) of the data set, the name of columns etc. The function size(train) is used to get the number of rows and columns of the data set and names(train) is used to get the names of columns(features).

The data set is not that large(only 614 rows) knowing the size of data set sometimes affect the choice of our algorithm. There are 13 columns(features) we have that is also not much, in case of a large number of features we go for techniques like dimensionality reduction etc. Let’s look at the first 10 rows to get a better feel of how our data looks like? The head(,n) function is used to read the first n rows of a dataset.
head(train, 10)
A number of preliminary inferences can be drawn from the above table such as:
Note that these inferences are just preliminary they will either get rejected or updated after further exploration.
I am interested in analyzing the LoanAmount column, let’s have a closer look at that.
describe(train[:LoanAmount])
It would provide the count(length), mean, median, minimum, quartiles and maximum in its output (Read this article to refresh basic statistics to understand population distribution).
Please note that we can get an idea of a possible skew in the data by comparing the mean to the median, i.e. the 50% figure.
For the non-numerical values (e.g. Property_Area, Credit_History etc.), we can look at frequency distribution to understand whether they make sense or not. The frequency table can be printed by the following command:
countmap ( train[:Property_Area])
Similarly, we can look at unique values of credit history. Note that dataframe_name[:column_name] is a basic indexing technique to access a particular column of the dataframe. A column can also be accessed by its index. For more information, refer to the documentation .
Another effective way of exploring the data is by doing it visually using various kind of plots as it is rightly said, “A picture is worth a thousand words” .
Julia doesn’t provide a plotting library of its own but it lets you use any plotting library of your own choice in Julia programs. In order to use this functionality you need to install the following package:
julia> Pkg.add(“Plots.jl”)
julia>Pkg.add(“StatPlots.jl”)
julia>Pkg.add(“PyPlot.jl”)The package “Plots.jl” provides a single frontend(interface) for any plotting library(matplotlib, plotly, etc.) you want to use in Julia. “StatPlots.jl” is a supporting package used for Plots.jl. “PyPlot.jl” is used to work with matplotlib of Python in Julia.
Now that we are familiar with basic data characteristics, let us study the distribution of various variables. Let us start with numeric variables – namely ApplicantIncome and LoanAmount
Let’s start by plotting the histogram of ApplicantIncome using the following commands:
using Plots, StatPlots #import required packages
pyplot() #Set the backend as matplotlib.pyplot
Plots.histogram(dropna(train[:ApplicantIncome]),bins=50,xlabel="ApplicantIncome",labels="Frequency") #Plot histogram
Here we observe that there are few extreme values. This is also the reason why 50 bins are required to depict the distribution clearly.
Next, we look at box plots to understand the distributions. Box plot for fare can be plotted by:
Plots.boxplot(dropna(train[:ApplicantIncome]), xlabel="ApplicantIncome")
This confirms the presence of a lot of outliers/extreme values. This can be attributed to the income disparity in the society. Part of this can be driven by the fact that we are looking at people with different education levels. Let us segregate them by Education:
Plots.boxplot(train[:Education],train[:ApplicantIncome],labels="ApplicantIncome")
We can see that there is no substantial difference between the mean income of graduate and non-graduates. But there are a higher number of graduates with very high incomes, which are appearing to be the outliers.
Now, Let’s look at the histogram and boxplot of LoanAmount using the following command:
Plots.histogram(dropna(train[:LoanAmount]),bins=50,xlabel="LoanAmount",labels="Frequency")
Plots.boxplot(dropna(train[:LoanAmount]), ylabel="LoanAmount")
Again, there are some extreme values. Clearly, both ApplicantIncome and LoanAmount require some amount of data munging. LoanAmount has missing and well as extreme values, while ApplicantIncome has a few extreme values, which demand deeper understanding. We will take this up in coming sections.
That was a lot of useful visualizations, to learn more about creating visualizations in Julia using Plots.jl Plots.jl Documentation.
Now’s the time where awesomeness of Plots.jl comes into play. The visualizations we created till now were all good but while exploration it is useful if the plot is interactive. We can create interactive plots in Julia using Plotly as a backend. Type the following code
plotly() #use plotly as backend
Plots.histogram(dropna(train[:ApplicantIncome]),bins=50,xlabel="ApplicantIncome",labels="Frequency")
You can do much more with Plots.jl and various backends it supports. Read Plots.jl Documentation 🙂
For those, who have been following, here you must wear your shoes to start running.
While our exploration of the data, we found a few problems in the data set, which needs to be solved before the data is ready for a good model. This exercise is typically referred as “Data Munging”. Here are the problems, we are already aware of:
In addition to these problems with numerical fields, we should also look at the non-numerical fields i.e. Gender, Property_Area, Married, Education and Dependents to see, if they contain any useful information.
Let us look at missing values in all the variables because most of the models don’t work with missing data and even if they do, imputing them helps more often than not. So, let us check the number of nulls / NaNs in the dataset
showcols(train)
Though the missing values are not very high in number, many variables have them and each one of these should be estimated and added to the data.
Note: Remember that missing values may not always be NaNs. For instance, if the Loan_Amount_Term is 0, does it makes sense or would you consider that missing? I suppose your answer is missing and you’re right. So we should check for values which are unpractical.
There are multiple ways of fixing missing values in a dataset. Take LoanAmount for example, there are numerous ways to fill the missing values – the simplest being replacement by the mean.
The other extreme would be to build a supervised learning model to predict loan amount on the basis of other variables and then use age along with other variables to predict survival.
We would be taking the simpler approach to fix missing values in this article:
#replace missing loan amount with mean of loan amount
train[isna.(train[:LoanAmount]),:LoanAmount] = floor(mean(dropna(train[:LoanAmount])))
#replace 0.0 of loan amount with the mean of loan amount
train[train[:LoanAmount] .== 0, :LoanAmount] = floor(mean(dropna(train[:LoanAmount])))
#replace missing gender with mode of gender values
train[isna.(train[:Gender]), :Gender] = mode(dropna(train[:Gender]))
#replace missing married with mode value
train[isna.(train[:Married]), :Married] = mode(dropna(train[:Married]))
#replace missing number of dependents with the mode value
train[isna.(train[:Dependents]),:Dependents]=mode(dropna(train[:Dependents]))
#replace missing values of the self_employed column with mode
train[isna.(train[:Self_Employed]),:Self_Employed]=mode(dropna(train[:Self_Employed]))
#replace missing values of loan amount term with mode value
train[isna.(train[:Loan_Amount_Term]),:Loan_Amount_Term]=mode(dropna(train[:Loan_Amount_Term]))
#replace credit history missing values with mode
train[isna.(train[:Credit_History]), :Credit_History] = mode(dropna(train[:Credit_History]))I have basically replaced all missing values in numerical columns with their means and with the mode in categorical columns. Let’s understand the code little closely,
train[isna.(train[:LoanAmount]),:LoanAmount] = floor(mean(dropna(train[:LoanAmount])))I hope this gives you a better understanding of the code part that is used to fix missing values.
As discussed earlier, there are better ways to perform data imputation and I encourage you to learn as many as you can. Get a detailed view of different imputation techniques through this article .
Now that we have fixed all missing values, we will be building a predictive machine learning model. We will also be cross-validating it and saving it to the disk for future use. The following packages are required for doing so:
julia> Pkg.add(“ScikitLearn.jl”)This package is an interface to Python’s scikit-learn package so python users are in for a treat. The interesting thing about using this package is you get to use the same models and functionality as you used in Python.
Sklearn requires all data to be of numeric type so let’s label encode our data,
using ScikitLearn
@sk_import preprocessing: LabelEncoder
labelencoder = LabelEncoder()
categories = [2 3 4 5 6 12 13]
for col in categories
train[col] = fit_transform!(labelencoder, train[col])
endThose who have used sklearn before will find this code to be familiar, we are using LabelEncoder to encode the categories. I have used the index of columns with categorical data.
Next, we will import the required modules. Then we will define a generic classification function, which takes a model as input and determines the Accuracy and Cross-Validation scores. Since this is an introductory article and julia code is very similar to python, I will not go into the details of coding. Please refer to this article for getting details of the algorithms with R and Python codes. Also, it’ll be good to get a refresher on cross-validation through this article , as it is a very important measure of power performance.
using ScikitLearn: fit!, predict, @sk_import, fit_transform!
@sk_import preprocessing: LabelEncoder
@sk_import model_selection: cross_val_score
@sk_import metrics: accuracy_score
@sk_import linear_model: LogisticRegression
@sk_import ensemble: RandomForestClassifier
@sk_import tree: DecisionTreeClassifier
function classification_model(model, predictors)
y = convert(Array, train[:13])
X = convert(Array, train[predictors])
X2 = convert(Array, test[predictors])
#Fit the model:
fit!(model, X, y)
#Make predictions on training set:
predictions = predict(model, X)
#Print accuracy
accuracy = accuracy_score(predictions, y)
println("\naccuracy: ",accuracy)
#5 fold cross validation
cross_score = cross_val_score(model, X, y, cv=5)
#print cross_val_score
println("cross_validation_score: ", mean(cross_score))
#return predictions
fit!(model, X, y)
pred = predict(model, X2)
return pred
endLet’s make our first Logistic Regression model. One way would be to take all the variables into the model but this might result in overfitting (don’t worry if you’re unaware of this terminology yet). In simple words, taking all variables might result in the model understanding complex relations specific to the data and will not generalize well. Read more about Logistic Regression .
We can easily make some intuitive hypothesis to set the ball rolling. The chances of getting a loan will be higher for:
So let’s make our first model with ‘Credit_History’.
model = LogisticRegression()
predictor_var = [:Credit_History]
classification_model(model, predictor_var)Accuracy : 80.945% Cross-Validation Score : 80.957%
#We can try a different combination of variables: predictor_var = [:Credit_History, :Education, :Married, :Self_Employed, :Property_Area] classification_model(model, predictor_var)
Accuracy : 80.945% Cross-Validation Score : 80.957%
Generally, we expect the accuracy to increase by adding variables. But this is a more challenging case. The accuracy and cross-validation score are not getting impacted by less important variables. Credit_History is dominating the mode. We have two options now:
A decision tree is another method for making a predictive model. It is known to provide higher accuracy than logistic regression model. Read more about Decision Trees.
model = DecisionTreeClassifier()
predictor_var = [:Credit_History, :Gender, :Married, :Education]
classification_model(model, predictor_var)Accuracy : 80.945% Cross-Validation Score : 76.656%
Here the model based on categorical variables is unable to have an impact because Credit History is dominating over them. Let’s try a few numerical variables:
#We can try different combinations of variables:
predictor_var = [:Credit_History, :Loan_Amount_Term]
classification_model(model, predictor_var)Accuracy : 99.345% Cross-Validation Score : 72.009%
Here we observed that although the accuracy went up on adding variables, the cross-validation error went down. This is the result of model over-fitting the data. Let’s try an even more sophisticated algorithm and see if it helps:
Random forest is another algorithm for solving the classification problem. Read more about Random Forest.
An advantage with Random Forest is that we can make it work with all the features and it returns a feature importance matrix which can be used to select features.
model = RandomForestClassifier(n_estimators=100)
predictors =[:Gender, :Married, :Dependents, :Education,
:Self_Employed, :Loan_Amount_Term, :Credit_History, :Property_Area,
:LoanAmount]
classification_model(model, predictors)Accuracy : 100.000% Cross-Validation Score : 78.179%
Here we see that the accuracy is 100% for the training set. This is the ultimate case of overfitting and can be resolved in two ways:
The updated code would now be
model = RandomForestClassifier(n_estimators=100, min_samples_split=25, max_depth=8, n_jobs=-1)
predictors = [:ApplicantIncome, :CoapplicantIncome, :LoanAmount, :Credit_History, :Loan_Amoun_Term, :Gender, :Dependents]
classification_model(model, predictors)Accuracy : 82.410% Cross-Validation Score : 80.635%
Notice that although accuracy reduced, the cross-validation score is improving showing that the model is generalizing well. Remember that random forest models are not exactly repeatable. Different runs will result in slight variations because of randomization. But the output should stay in the ballpark.
You would have noticed that even after some basic parameter tuning on the random forest, we have reached a cross-validation accuracy only slightly better than the original logistic regression model. This exercise gives us some very interesting and unique learning:
So are you ready to take on the challenge? Start your data science journey with Loan Prediction Problem.
Julia is a powerful language with interesting libraries but it may so happen that you want to use library of your own from outside Julia. One such reason can be lack of functionality in existing Julia libraries(it is still very young). For situations like this, Julia provides ways to call libraries from R and Python. Let’s see how can we do that?
Install the following package:
julia> Pkg.add("PyCall.jl")using PyCall
@pyimport pandas as pd
df = pd.read_csv("train.csv")There is something interesting about using a Python library as smoothly in another language.
Pandas is a very mature and performant library, it is certainly a bliss that we can use it wherever the native DataFrames.jl falls short.
Install the following packages:
julia> Pkg.add("RDatsets.jl")
julia> Pkg.add("RCall.jl")using RCall, RDatasets
mtcars = datasets("datasets", "mtcars");
library(ggplot2)
ggplot($mtcars, aes(x = WT, y=MPG)) + geom_point()
This tutorial aims to enhance your efficiency in starting data science with Julia. It not only introduces basic data analysis methods but also demonstrates the implementation of advanced techniques. Julia is gaining popularity among data scientists due to its ease of learning, integration capabilities, speed akin to C, and compatibility with R and Python libraries. Mastering Julia enables the full data science project life-cycle, encompassing data reading, analysis, visualization, and prediction. Access the GitHub repository for all code used in this article. For any challenges or feedback, feel free to share in the comments below. Embrace learning, engagement, competition, and career growth by joining our BlackBelt Program.
A. Yes, Julia is designed for ease of learning, with its clean syntax and support for high-level mathematical operations, making it accessible for newcomers.
A. Julia shares some similarities with MATLAB, such as its numerical computing capabilities and matrix operations, but it offers greater flexibility and performance.
A. Julia’s learning curve is comparable to Python’s, and its syntax is intuitive. While both languages are user-friendly, Julia’s speed and specific features might influence preference.
A. Yes, Julia often outperforms Python due to its just-in-time (JIT) compilation, making it suitable for high-performance computing tasks and data-intensive applications.
Lorem ipsum dolor sit amet, consectetur adipiscing elit,
Very interesting paper! This will encourage me to learn Julia. Basically I am a Python & R programmer. Thanks!
Hey Jacques, Exactly! It is very comfortable for people coming from those backgrounds. This is just the surface, once you get comfortable with the language, you can take advantage of its niche features, like training your model parallelly etc. Cheers, Sanad
After typing the command: julia> Pkg.add(“IJulia”), pressed Enter. Immediately below info messages appeared - INFO: Initializing package repository C:\Users\Sree\.julia\v0.6 INFO: Cloning METADATA from https://github.com/JuliaLang/METADATA.jl and nothing happened in last 10 mins ? Is it still working? Should I expect something after a while? How long before i can get to next step?
Hey vc, Pkg.add() command fetched various package files and their dependencies in the background and installs them on your computer. For this, you need an active internet connection. If your internet is slow, you might have to wait for little longer. Also, I have updated the article with a screenshot of the above. Hope this helps, Sanad
Good article Sanad,thanks a lot....also please include in this article any small data science project implementation along with data set so that we can relate quickly with all above concepts. I am from dataware house background and just curious about data science field.
Hey Sushil, Thanks for your feedback! Though I would like to inform you that I have taken an example dataset in the above article and shown how you perform analysis on the same. Cheers, Sanad
Hi Sanad, Good article, nicely put and thanks for breaking everything into bits and pieces. It would be of great help if you can give a bit more about why to use Julia, for instance you mentioned that "you can take advantage of its niche features, like training your model parallelly etc." . A bit more of these. Good work and keep it up!
Hey Kamaraju, thanks for the feedback! If you want a high-level view of "Why Julia?" you can check out this article https://www.analyticsvidhya.com/blog/2015/07/julia-language-getting-started/ Surely, I am looking forward to getting into depths of Julia in my upcoming articles, would love to share those as and when they are complete. Sanad
Your first data structure actually does not produce a 1D vector, but a 2D Array. For 1D vector use comma's like [1,2,4]
Hey Ken, Thanks for pointing it out! I just realized that it was evident in the output(the dimensions of the array). I have updated the code. Cheers :) Sanad
Julia is great not just for technical/numerical/scientific computing either. As a long-time C/C++ programmer (with CachéObjectScript and Python experience also), I've found Julia to be much more productive than C or C++ for my general programming tasks, while still giving me the performance I need.
Hey Scott, Thanks for your inputs! It's always good to get different perspectives from folks in the industry! :D Cheers, Sanad
Sanad, Running into problems here in the Logistic Regression. When you run the below cell: #We can try a different combination of variables: predictor_var = [:Credit_History, :Education, :Married, :Self_Employed, :Property_Area] classification_model(model, df,predictor_var,outcome_var) I get the following error: UndefVarError: outcome_var not defined Stacktrace: [1] include_string(::String, ::String) at .\loading.jl:522 You did not have the outcome_var in the original classification_model definition. Di not know how to resolve this as this definition here is a different set of arguments. Was going great till now. Any help would be appreciated!! Srikar
Hey Srikar, Thanks for pointing it out! It was a typo that has been duly updated. Please let me know if you have any other doubts Cheers! Sanad :)
thanks srikar
Hi Sanad, Thanks for your reply. One more issue i noticed in the cell below: #We can try different combinations of variables: predictor_var = [:Credit_History, :Loan_Amount_Term, :LoanAmount_log] classification_model(model, predictor_var) There is no LoanAmount_log in the data set you specified. Also when i try the following cell as per the tutorial: ## We can try a different combination of variables: predictor_var = [:Credit_History, :Education, :Loan_Amount_Term] classification_model(model, predictor_var) This is what i get as results, and no idea how to decipher the error!! Any help is immensely apreciated. accuracy: 0.8127035830618893 cross_validation_score: 0.7949497620306716 PyError (ccall(@pysym(:PyObject_Call), PyPtr, (PyPtr, PyPtr, PyPtr), o, arg, C_NULL)) ValueError('could not convert string to float: Graduate',) File "C:\Users\sbellur\.julia\v0.6\Conda\deps\usr\lib\site-packages\sklearn\tree\tree.py", line 412, in predict X = self._validate_X_predict(X, check_input) File "C:\Users\sbellur\.julia\v0.6\Conda\deps\usr\lib\site-packages\sklearn\tree\tree.py", line 373, in _validate_X_predict X = check_array(X, dtype=DTYPE, accept_sparse="csr") File "C:\Users\sbellur\.julia\v0.6\Conda\deps\usr\lib\site-packages\sklearn\utils\validation.py", line 433, in check_array array = np.array(array, dtype=dtype, order=order, copy=copy) Stacktrace: [1] pyerr_check at C:\Users\sbellur\.julia\v0.6\PyCall\src\exception.jl:56 [inlined] [2] pyerr_check at C:\Users\sbellur\.julia\v0.6\PyCall\src\exception.jl:61 [inlined] [3] macro expansion at C:\Users\sbellur\.julia\v0.6\PyCall\src\exception.jl:81 [inlined] [4] #_pycall#67(::Array{Any,1}, ::Function, ::PyCall.PyObject, ::Array{Any,2}, ::Vararg{Array{Any,2},N} where N) at C:\Users\sbellur\.julia\v0.6\PyCall\src\PyCall.jl:653 [5] _pycall(::PyCall.PyObject, ::Array{Any,2}, ::Vararg{Array{Any,2},N} where N) at C:\Users\sbellur\.julia\v0.6\PyCall\src\PyCall.jl:641 [6] #pycall#71(::Array{Any,1}, ::Function, ::PyCall.PyObject, ::Type{PyCall.PyAny}, ::Array{Any,2}, ::Vararg{Array{Any,2},N} where N) at C:\Users\sbellur\.julia\v0.6\PyCall\src\PyCall.jl:675 [7] pycall(::PyCall.PyObject, ::Type{PyCall.PyAny}, ::Array{Any,2}, ::Vararg{Array{Any,2},N} where N) at C:\Users\sbellur\.julia\v0.6\PyCall\src\PyCall.jl:675 [8] #call#72(::Array{Any,1}, ::PyCall.PyObject, ::Array{Any,2}, ::Vararg{Array{Any,2},N} where N) at C:\Users\sbellur\.julia\v0.6\PyCall\src\PyCall.jl:678 [9] (::PyCall.PyObject)(::Array{Any,2}, ::Vararg{Array{Any,2},N} where N) at C:\Users\sbellur\.julia\v0.6\PyCall\src\PyCall.jl:678 [10] #predict#26(::Array{Any,1}, ::Function, ::PyCall.PyObject, ::Array{Any,2}, ::Vararg{Array{Any,2},N} where N) at C:\Users\sbellur\.julia\v0.6\ScikitLearn\src\Skcore.jl:95 [11] classification_model(::PyCall.PyObject, ::Array{Symbol,1}) at .\In[41]:32 [12] include_string(::String, ::String) at .\loading.jl:522
Hey Srikar, 1. Thanks for pointing out the typo, it has been updated. 2. This can be a very good case study for you to learn about python errors, look closely at the error message and you will find this line to be the most related to your model: ValueError(‘could not convert string to float: Graduate’,) Python gives "ValueError" whenever type mismatch happens. If you read the error message further, you'll notice it says "could not convert a string to float: Graduate". What this means is our Education column has not been label encoded, so we have strings like "Graduate" and "Not Graduate" in the column while sklearn "expects numerical values". The solution for this will be to : 1. Re-run the label encoding code 2. Check your train[:Education] column if it is properly encoded 3. Run the model training code Hope this helps, Sanad :D
Okay! I'm seriously considering learning Julia, being a python programmer, I wanted to know how natural the shift is? Is the speed worth the learning curve? Appreciate any thoughts.
Hey Venkatesh, I honestly didn't face much of a learning curve on transitioning from Python to Julia, if you closely look at the tutorial you'll notice it too. But that said, if you really wanna learn a language you'd have to go a bit deeper Hope that helps, Sanad :)
Hi, I'm pretty new to data science, with a programming background only in C, C++, C# and Matlab. currently I'm training myself the basic concepts of the field and learning to get comfortable with Python (and eventually go for R to make myself more versatile) with that in mind, plus things you say about Julia(somehow convincing), can I just skip learning Python, forget about versatility and just start to learn Julia right away without worrying about other languages used in Data Science? In other words, can this programming language be used as a complete substitute to either R or Python, so I can save more time for the core concepts of Data Science?
I feel that is oone of the soo muich vital info for me. Annd i'm glad reading your article. But wanna statement on few normal issues, The website style is wonderful, the articles is actually great : D. Just right job, cheers
Hi Sanad, I am facing issues in Julia Package installation. I keep waiting and yet it does not move to installing the IJulia Package. Please advice
We are unable to download data(train.csv). could you please provide the link to download it.
Hi Nitesh, I just checked and the link works fine for me. The link provided in the blog will take you to the loan prediction problem. Please register yourself in the same. Once you do that, you will be able to view the train and test csv files at the bottom of the page. If you face any issue, please let us know.
New to Julia and using 1.9.3 (and to modeling, although I have some Python and R experience) which has been quite different in many ways from the earlier versions. I'm having trouble with this bit of code: model = LogisticRegression() predictor_var = convert(Array, train[!,:Credit_History]) classification_model(model, predictor_var) The original column-only indexing of {:Credit_History} does not work and I can't find any reference on how to make this work, or generalize it to a list of predictor variables. Any help available? Thanks. to correctly specify the predictor variable(s) for logistic regression using Scikit Learn.
I'm new to Julia but have worked with both Python and R. I'm wondering if there's any help available on the tutorial. I'm following it through using 1.9.3. I've managed to load all the packages and adjust the indexing as I've gone through, but I get stuck trying to pass a column list of predictor variables in the logistic regression section: model = LogisticRegression() predictor_var = [:Credit_History] classification_model(model, predictor_var) The "[:column_name]" syntax is deprecated and I can't figure out how to adjust it so I can pass one (or more) columns in the predictor_var variable. Thanks.