Introduction
In this tutorial, we delve into the intricacies of Binary Cross Entropy (BCE) and its pivotal role in optimizing machine learning models, particularly within the realms of Python-based regression and neural networks. By understanding how BCE measures the dissimilarity between predicted and actual probability distributions, you’ll gain insight into enhancing your model’s accuracy for positive class identification. We’ll explore the algorithm’s application, the significance of batch size in training, and the mathematical foundation underpinning this essential evaluation metric. Join us as we uncover the mechanisms behind BCE and its impact on model optimization.
In this article, you will get about the binary cross entropy, binary cross entropy loss function, and binary classification loss these will cover ij this article and you will get full understanding about the binary cross entropy.
Learning Outcomes
- Gain a comprehensive understanding of what a classification model is and how it differs from other types of models in data science.
- Learn about different types of classifiers and their applications in various data science frameworks.
- Get familiar with popular machine learning frameworks such as TensorFlow, Keras, and PyTorch, and understand how they facilitate model building and optimization.
- Learn the principles of gradient descent and its application in optimizing classification models, including logistic regression.
- Explore the softmax function and its use in converting model’s predictions into probabilities for multi-class classification problems.
- Gain proficiency in using NumPy for numerical operations essential in machine learning, such as handling tensors and matrices.
- Learn the importance of logarithmic functions in calculating loss functions such as binary and categorical cross-entropy.
- Understand KL divergence and its role in measuring the difference between probability distributions, aiding in the fine-tuning of classification models.
- Learn how to manage classification problems with a varying number of classes, and how this affects the computation of loss and model training.
Table of contents
What is Binary Classification?
Binary Classification is a problem where we have to segregate our observations in any of the two labels on the basis of the features. Suppose you have some images now you have to put each of them in a stack one for Dogs and the other for the Cats. Here you are solving a binary classification problem.

Similarly, if a machine learning model is identifying mails as ham or spam, it is performing binary classification as it is dividing the objects into two classes.
Introduction to Loss function
Before jumping into Log Loss let’s first understand what is Loss function. Imagine the scenario, Once you developed your machine learning model that you believe, successfully identifying the cats and dogs but how do you know this is the best result?
Here, we are looking for the metrics or a function that we can use to optimize our model performance. The loss function tells how good your model is in predictions. If the model predictions are closer to the actual values the Loss will be minimum and if the predictions are totally away from the original values the loss value will be the maximum.
In mathematical connotations
Loss= abs(Y_pred – Y_actual)
On the basis of the Loss value, you can update your model until you get the best result.
In this article, we will specifically focus on Binary Cross Entropy also known as Log loss, it is the most common loss function used for binary classification problems.
What is Binary Cross Entropy Or Logs Loss?
Binary Cross Entropy is a loss function used in machine learning and deep learning to measure the difference between predicted binary outcomes and actual binary labels. It quantifies the dissimilarity between probability distributions, aiding model training by penalizing inaccurate predictions. It’s widely used in tasks like binary classification, where the goal is to categorize data into two classes.
Binary Cross Entropy, also known as Binary Log Loss or Binary Cross-Entropy Loss, is a commonly used loss function in machine learning, particularly in binary classification problems. It is designed to measure the dissimilarity between the predicted probability distribution and the true binary labels of a dataset.
Binary cross entropy compares each of the predicted probabilities to actual class output which can be either 0 or 1. It then calculates the score that penalizes the probabilities based on the distance from the expected value. That means how close or far from the actual value.
Let’s first get a formal definition of binary cross-entropy
Binary Cross Entropy is the negative average of the log of corrected predicted probabilities.
Right Now, don’t worry about the intricacies of the definition, we will understand that in a while. Just look at the example below.
Predicted Probabilities

Here in the table, we have three columns
ID: It represents a unique instance.
Actual: It is the class the object originally belongs to.
Predicted_probabilities.: The is output given by the model that tells, the probability object belongs to class 1.

Corrected Probabilities
Now you might have a question, what are corrected probabilities? It is the probability that a particular observation belongs to its original class. As shown in the above image, ID6 originally belongs to class 1 hence its predicted probability and corrected probability is the same i.e 0.94.
On the other hand, the observation ID8 is from class 0. In this case, the predicted probability i.e the chances that ID8 belongs to class 1 is 0.56 whereas, the corrected probability means the chances that ID8 belongs to class 0 is ( 1-predicted_probability) is 0.44. In the same way, corrected probabilities of all the instances will be calculated.
Log(Corrected probabilities)
Now we will calculate the log value for each of the corrected probabilities. The reason behind using the log value is, the log value offers less penalty for small differences between predicted probability and corrected probability. when the difference is large the penalty will be higher.

Here we have calculated log values for all the corrected probabilities. Since all the corrected probabilities lie between 0 and 1, all the log values are negative.
In order to compensate for this negative value, we will use a negative average of the values

The value of the negative average of corrected probabilities we calculate comes to be 0.214 which is our Log loss or Binary cross-entropy for this particular example.
Further, instead of calculating corrected probabilities, we can calculate the Log loss using the formula given below.

Here, pi is the probability of class 1, and (1-pi) is the probability of class 0.
When the observation belongs to class 1 the first part of the formula becomes active and the second part vanishes and vice versa in the case observation’s actual class are 0. This is how we calculate the Binary cross-entropy.
Binary Cross Entropy for Multi-Class classification
If you are dealing with a multi-class classification problem you can calculate the Log loss in the same way. Just use the formula given below.
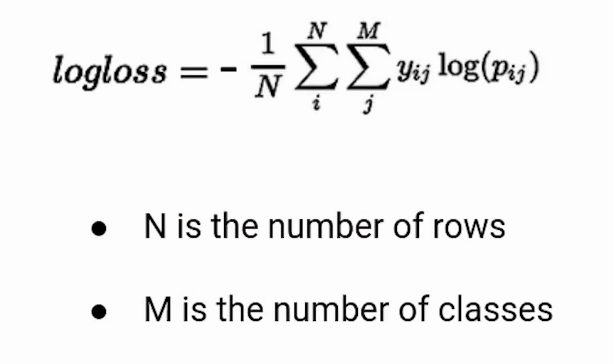
What is the Binary Cross Entropy Formula?
The Binary Cross Entropy Formula looks like this:
BCE = – ( y * log(y_pred) + (1 – y) * log(1 – y_pred) )
Here is what is that means:
BCE: Binary Cross Entropy
y: True label (either 0 or 1)
y_pred: Predicted probability (between 0 and 1)
log: Natural logarithm (usually base-e logarithm)
This formula calculates the loss for each individual sample and then averages them for all samples in your dataset.
Conclusion
Mastering the fundamentals of classification models and their evaluation metrics is crucial for any data science professional. Understanding how activation functions transform logits into probabilities and the role of categorical cross-entropy loss in measuring the dissimilarity between predicted values and the true label ensures precise model optimization. Additionally, recognizing the importance of metrics like MSE for regression tasks and the differentiation between positive and negative classes enhances your ability to handle complex problems, including image segmentation. This comprehensive knowledge empowers you to build more accurate and efficient machine learning models.Understand about the Binary cross entropy its uses and Binary cross entropy formula. Also, by reading this we hope you clear your understanding about the binary cross entropy loss function, binary classification loss and binary cross entropy loss.
Key Takeaways
- Mastering classification models, including logistic regression and neural networks, is essential for accurate predictions and effective model performance in data science.
- Activation functions transform logits into probabilities, aiding in the accurate classification of data into positive and negative classes.
- Familiarity with evaluation metrics like MSE for regression tasks and categorical cross-entropy for classification enhances model assessment and improvement strategies.
- Understanding the segmentation process in tasks like image classification improves the precision of machine learning applications.
- Techniques such as gradient descent are vital for minimizing loss functions and optimizing the performance of classification models.
Frequently Asked Questions
A. Binary Cross Entropy is used for binary classification tasks with two classes, while Categorical Cross Entropy is used for multiclass classification tasks with more than two classes. The choice of loss function depends on the specific problem and the number of classes involved.
A. Binary cross entropy, also referred to as logarithmic loss or log loss, is a metric used to evaluate models by measuring the extent of incorrect labeling of data classes. It penalizes the model for deviations in probability that result in misclassification of the labels. When the log loss value is low, it indicates a high level of accuracy in the model’s predictions.
In Keras, binary cross-entropy loss helps train models for binary classification tasks (e.g., spam detection). It measures the difference between what the model predicts (probability) and the actual labels (0 or 1). The model minimizes this loss to improve its predion.
A good binary cross-entropy loss depends on your problem. Here’s a quick guide:
< 0.05: Great
< 0.20: Good
> 0.30: Not ideal
> 1.00: Very poor
If you are looking to kick start your Data Science Journey and want every topic under one roof, your search stops here. Check out Analytics Vidhya’s Certified AI & ML BlackBelt Plus Program.








I am lost under heading of Corrected probabilities "On the other hand, the observation ID8 is from class 0. In this case, the predicted probability i.e the chances that ID8 belongs to class 1 is 0.56 whereas, the corrected probability means the chances that ID8 belongs to class 0 is (1-predicted_probability) is 0.44. In the same way, corrected probabilities of all the instances will be calculated." In above paragraph why are you calculating corrected probability using (1-predicted_probability)?
This is clearly written with ChatGPT