Interview Prep
Career
GenAI
Prompt Engg
ChatGPT
LLM
Langchain
RAG
AI Agents
Machine Learning
Deep Learning
GenAI Tools
LLMOps
Python
NLP
SQL
AIML Projects

Reading list

Machine Learning Basics for a Newbie
6 Steps of Machine learning Lifecycle Introduction to Predictive Modeling
Introduction to Exploratory Data Analysis & Data Insights Descriptive Statistics Inferential Statistics How to Understand Population Distributions?
Reading Data Files into Python Different Variable Datatypes
Probability for Data Science Basic Concepts of Probability Axioms of Probability Conditional Probability
Central Tendencies for Continuous Variables Spread of Data KDE plots for Continuous Variable Overview of Distribution for Continuous variables Normal Distribution Skewed Distribution Skeweness and Kurtosis Distribution for Continuous Variable
Central Tendencies for Categorical Variables Understanding Discrete Distributions Performing EDA on Categorical Variables
Dealing with Missing Values Understanding Outliers Identifying Outliers in Data Outlier Detection in Python Outliers Detection Using IQR, Z-score, LOF and DBSCAN
Sample and Population Central Limit Theorem Confidence Interval and Margin of Error
Bivariate Analysis Introduction
Covariance Pearson Correlation Spearman's Correlation & Kendall's Tau Correlation versus Causation Tabular and Graphical methods for Bivariate Analysis Performing Bivariate Analysis on Continuous-Continuous Variables
Tabular and Graphical methods for Continuous-Categorical Variables Introduction to Hypothesis Testing P-value Two sample Z-test T-test T-test vs Z-test Performing Bivariate Analysis on Continuous-Catagorical variables
Chi-Squares Test Bivariate Analysis on Categorical Categorical Variables
Multivariate Analysis A Comprehensive Guide to Data Exploration The Data Science behind IPL
Supervised Learning vs Unsupervised Learning Reinforcement Learning Generative and Descriminative Models Parametric and Non Parametric model
Machine Learning Pipeline Preparing Dataset Build a Benchmark Model: Regression Build a Benchmark Model: Classification
Evaluation Metrics for Machine Learning Everyone should know Confusion Matrix Accuracy Precision and Recall AUC-ROC Log Loss R2 and Adjusted R2
Dealing with Missing Values Replacing Missing Values Imputing Missing Values in Data Working with Categorical Variables Working with Outliers Preprocessing Data for Model Building
Understanding Cost Function Understanding Gradient Descent Math Behind Gradient Descent Assumptions of Linear Regression Implement Linear Regression from Scratch Train Linear Regression in Python Implementing Linear Regression in R Diagnosing Residual Plots in Linear Regression Models Generalized Linear Models Introduction to Logistic Regression Odds Ratio Implementing Logistic Regression from Scratch Introduction to Scikit-learn in Python Train Logistic Regression in python Multiclass using Logistic Regression How to use Multinomial and Ordinal Logistic Regression in R ? Challenges with Linear Regression Introduction to Regularisation Implementing Regularisation Ridge Regression Lasso Regression
Introduction to K Nearest Neighbours Determining the Right Value of K in KNN Implement KNN from Scratch Implement KNN in Python
Bias Variance Tradeoff Introduction to Overfitting and Underfitting Visualizing Overfitting and Underfitting Selecting the Right Model What is Validation? Hold-Out Validation Understanding K Fold Cross Validation
Introduction to Feature Selection Feature Selection Algorithms Missing Value Ratio Low Variance Filter High Correlation Filter Backward Feature Elimination Forward Feature Selection Implement Feature Selection in Python Implement Feature Selection in R
Introduction to Decision Tree Purity in Decision Tree Terminologies Related to Decision Tree How to Select Best Split Point in Decision Tree? Chi-Squares Information Gain Reduction in Variance Optimizing Performance of Decision Tree Train Decision Tree using Scikit Learn Pruning of Decision Trees
Introduction to Feature Engineering Feature Transformation Feature Scaling Feature Engineering Frequency Encoding Automated Feature Engineering: Feature Tools
Introduction to Naive Bayes Conditional Probability and Bayes Theorem Introduction to Bayesian Adjustment Rating: The Incredible Concept Behind Online Ratings! Working of Naive Bayes Math behind Naive Bayes Types of Naive Bayes Implementation of Naive Bayes
Understanding how to solve Multiclass and Multilabled Classification Problem Evaluation Metrics: Multi Class Classification
Introduction to Ensemble Techniques Basic Ensemble Techniques Implementing Basic Ensemble Techniques Finding Optimal Weights of Ensemble Learner using Neural Network Why Ensemble Models Work well?
Introduction to Stacking Implementing Stacking Variants of Stacking Implementing Variants of Stacking Introduction to Blending Bootstrap Sampling Introduction to Random Sampling Hyper-parameters of Random Forest Implementing Random Forest Out-of-Bag (OOB) Score in the Random Forest IPL Team Win Prediction Project Using Machine Learning Introduction to Boosting Gradient Boosting Algorithm Math behind GBM Implementing GBM in python Regularized Greedy Forests Extreme Gradient Boosting Implementing XGBM in python Tuning Hyperparameters of XGBoost in Python Implement XGBM in R/H2O Adaptive Boosting Implementing Adaptive Boosing LightGBM Implementing LightGBM in Python Catboost Implementing Catboost in Python
Different Hyperparameter Tuning methods Implementing Different Hyperparameter Tuning methods GridsearchCV RandomizedsearchCV Bayesian Optimization for Hyperparameter Tuning Hyperopt
Understanding SVM Algorithm SVM Kernels In-depth Intuition and Practical Implementation SVM Kernel Tricks Kernels and Hyperparameters in SVM Implementing SVM from Scratch in Python and R
Introduction to Principal Component Analysis Steps to Perform Principal Compound Analysis Computation of Covariance Matrix Finding Eigenvectors and Eigenvalues Implementing PCA in python Visualizing PCA A Brief Introduction to Linear Discriminant Analysis Introduction to Factor Analysis
Introduction to Clustering Applications of Clustering Evaluation Metrics for Clustering Understanding K-Means Implementation of K-Means in Python Implementation of K-Means in R Choosing Right Value for K Profiling Market Segments using K-Means Clustering Hierarchical Clustering Implementation of Hierarchial Clustering DBSCAN Defining Similarity between clusters Build Better and Accurate Clusters with Gaussian Mixture Models
Understand Basics of Recommendation Engine with Case Study
8 Ways to Improve Accuracy of Machine Learning Models
Introduction to Dask Working with CuML
Introduction to Machine Learning Interpretability Framework and Interpretable Models model Agnostic Methods for Interpretability Implementing Interpretable Model Understanding SHAP Out-of-Core ML Introduction to Interpretable Machine Learning Models Model Agnostic Methods for Interpretability Game Theory & Shapley Values
Introduction to Machine Learning Interpretability Framework and Interpretable Models model Agnostic Methods for Interpretability Implementing Interpretable Model Understanding SHAP Out-of-Core ML Introduction to Interpretable Machine Learning Models Model Agnostic Methods for Interpretability Game Theory & Shapley Values
Introduction to AutoML Implementation of MLBox Introduction to PyCaret TPOT Auto-Sklearn EvalML
Pickle and Joblib Introduction to Model Deployment
Deploying Machine Learning Model using Streamlit Deploying ML Models in Docker Deploy Using Streamlit Deploy on Heroku Deploy Using Netlify Introduction to Amazon Sagemaker Setting up Amazon SageMaker Using SageMaker Endpoint to Generate Inference Deploy on Microsoft Azure Cloud Introduction to Flask for Model Deploying ML model using Flask
Model Deployment in Android Model Deployment in Iphone

How to find inefficient branches when considering multiple outputs?

Tavish Srivastava
Tavish Srivastava Last Updated : 28 Apr, 2015
5 min read

Recently, I was working on a business problem, which required me to find out inefficient branches of a bank X in North America and find root cause of their inefficiencies.

I had solved several root cause analysis problems in past but finding a quantitative parameter for efficiency was new to me. This was a complex task because efficiency was derived from multiple target variables such as branch revenue vs. capacity, customer satisfaction index, policy persistency etc. Can we assign some weights to each of the target variable and sum them to get efficiency? But how will we get such weights? Is there a scientific way to get these weight?

I did a small research and found a method using simplex programming to obtain efficiency in problems involving multiple input and output parameters. This technique is commonly known as Data Envelopment Analysis. Even though its a popular technique in OR, it is not very common in analytics industry. This article will give you a brief layout of the formulation and explain its utility by a business case.

efficiency

[stextbox id=”section”]Lets start with a simple example:[/stextbox] 

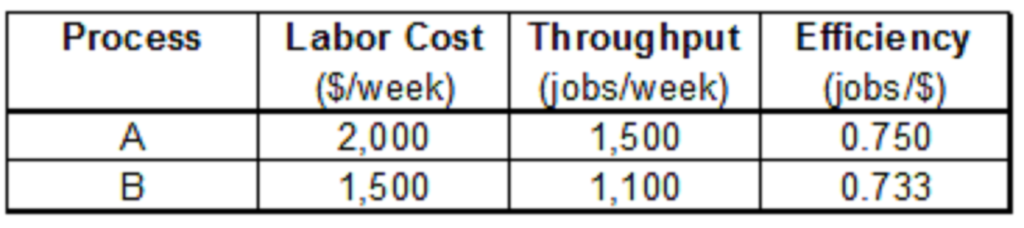
We have two processes A and B. Each process manufacture some jobs/week. And both jobs have different labor cost. As we know efficiency is a ratio of output and input, two processes will be compared based on their efficiency.Following are some illustrative figures:

eg1

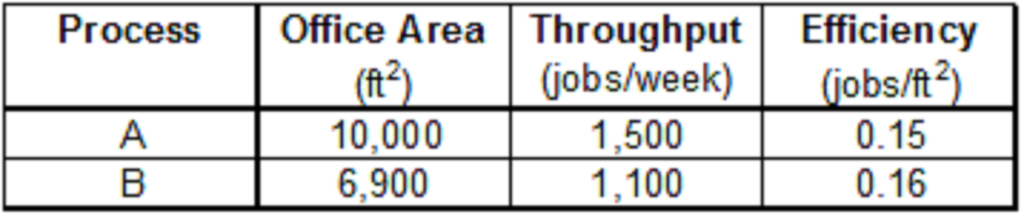
Comparing the two efficiency, it can easily be concluded that Process A is more efficient than process B. That was easy! Lets make it slightly more complicated.  Labor Cost might not be the only cost involved. The above analysis assumes that all other costs are similar for the two processes. Lets introduce an additional cost i.e. office rent. Now office rent is proportional to office premise area. Following are some illustrative figures:

eg2

The efficiency figures are now swapped. Process B seems to be more efficient when only office Area costs are considered. Now in this case, we know the office rent/square feet. Hence we can calculate the total cost, i.e. sum of Office rent/week and labor cost/week. And determine total efficiency of the two processes using total costs.

What made the determination easy for this case? We already knew the weights to be applied on each of the input variable i.e. Office Area and Labor cost. The weight for Office area was rent/square feet and that of labor cost was one.

[stextbox id=”section”]Lets complicate the puzzle further:[/stextbox] 

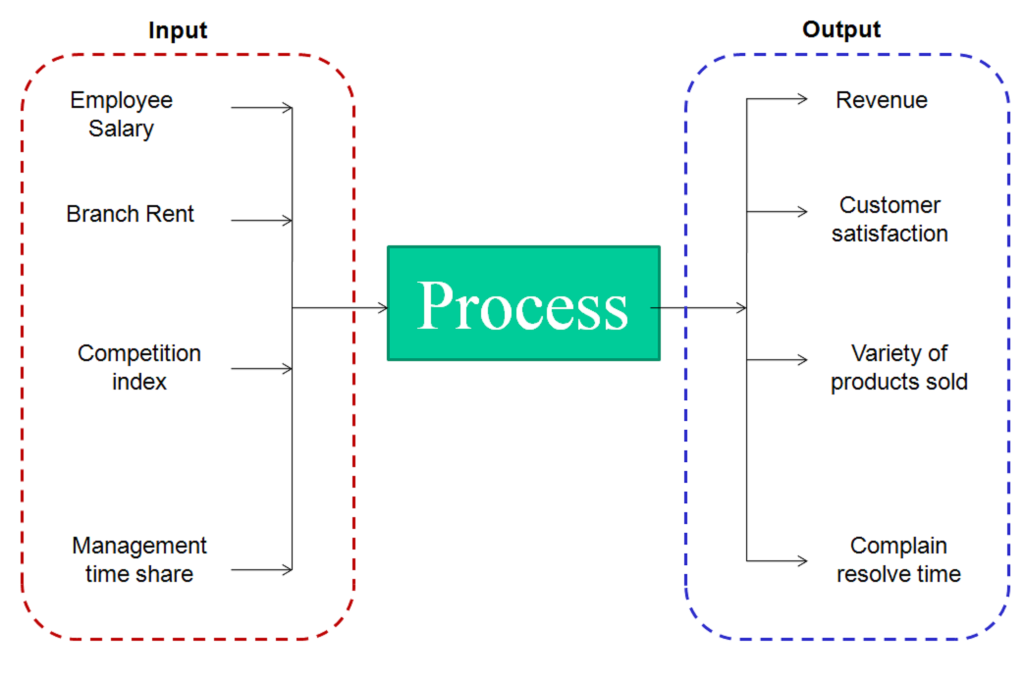
The output in this case was simply throughput. In a real life scenario, the inputs and outputs are non comparable parameters. Lets take example of a bank branches. The objective is to compare the branch efficiency and find the most efficient branch. Following are some of the identified input and output parameter of these branches :

Process

First step in any efficiency problem is to identify independent inputs and outputs. Make sure that the inputs and outputs are independent variables. In the above scenario, Employee salary and Branch Rent is in terms of dollars, Competition index (Degree of competition in locality) is an index and Management time share is a percentage term. Clearly Input variables are non additive. Similarly, output parameters are non-additive as well. We will derive an effectiveness of each branch using all these variables.

[stextbox id=”section”]Know the Maths behind:[/stextbox] 

The DEA technique is a kind of simple linear programming. It assumes certain aspects and knowing these aspects is essential before applying the technique. The formulation will make the assumptions clear. Following are the abbreviations used in this formulation :

1. Formulation is done for p processes

2. in(i,k) is the i th input parameter for the k th process

3. out(j,k) is the j th output parameter for the k th process

4. win(i) is the weight of i th input parameter

5. wout(j) is the weight of jth output parameter

FormulationSolving the above equations will give us efficiency of each business unit (branch in this case). The solution will also give the relative importance of each input and output parameter. The assumptions in this formulation are :

1. The Input and Output of each business unit are linear functions.

2. Each of input and output variables are independent of each other

3. Input and Output variables are exhaustive

 [stextbox id=”section”] Lets find efficiency graphically:[/stextbox] 

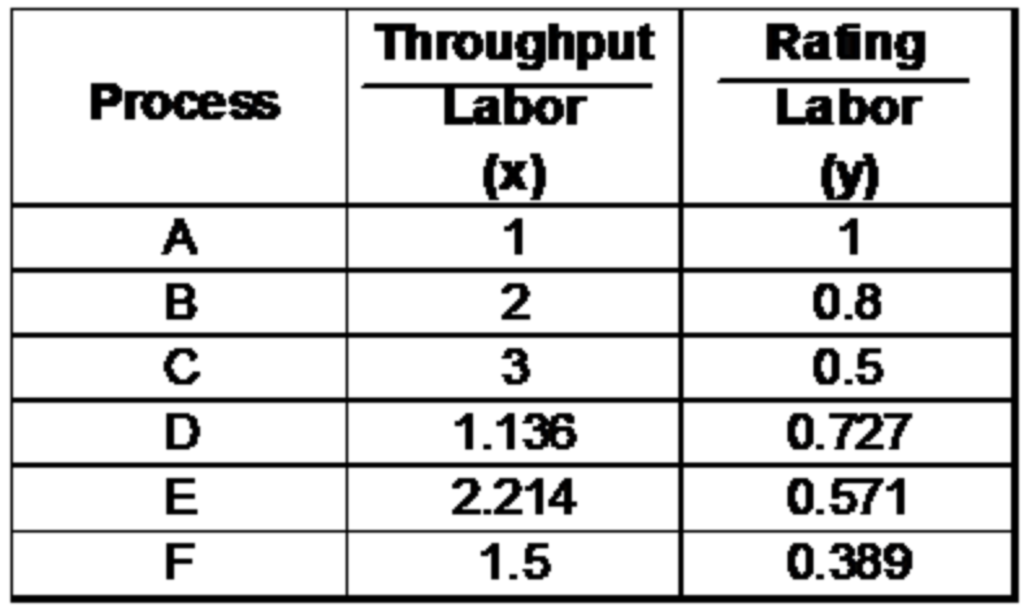
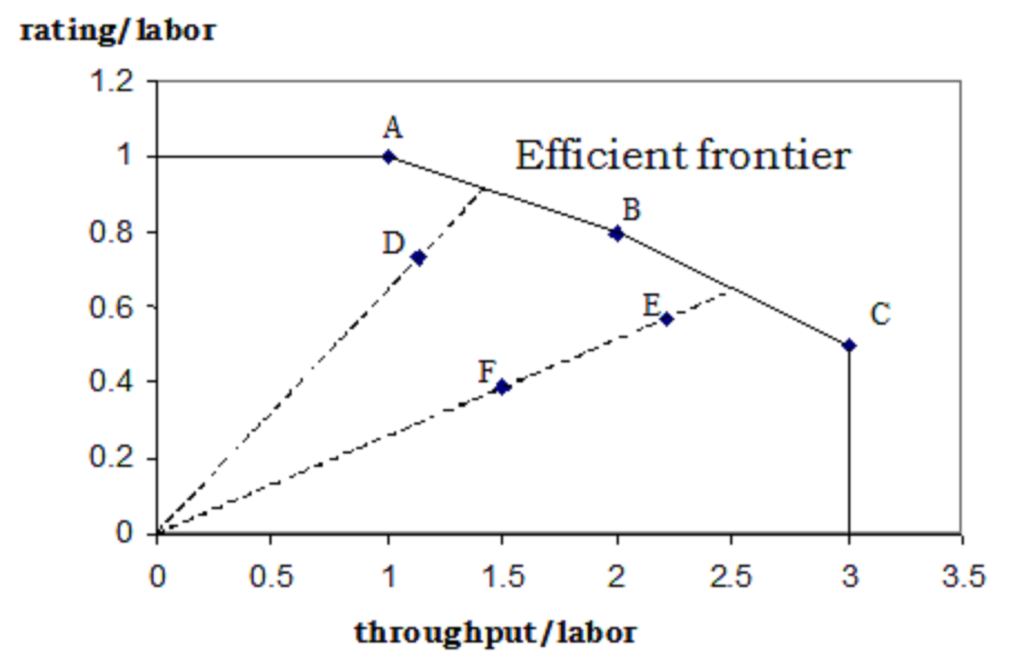
Suppose following are the input and output variables of 6 Processes :

Exam1

We define the two independent efficiency based on the two output parameters,

Exam2

Lets plot the two efficiency graphically.

DEA

As the name suggests, DEA defines an envelope of 100% efficiency. ABC is the envelope and any point inside the envelope is an inefficient unit.The graphical representation was easy for a two dimensional problem. But for the bank branch problem discussed in the last section, we will have to draw a 9 ( 4-1 *  4-1) dimensional envelope and hence very difficult to visualize.

[stextbox id=”section”]Advantages of DEA technique:[/stextbox] 

Following are the advantages of the technique :

1. No need to explicitly specify a mathematical form for the production function
—2. It is proven to be useful in uncovering relationships that remain hidden for other methodologies
—3. It is capable of handling multiple inputs and outputs
—4. It is capable of being used with any input-output measurement
—5. The sources of inefficiency can be analyzed and quantified for every evaluated unit
[stextbox id=”section”]Final notes:[/stextbox] 
DEA is a very useful technique when it comes to comparing efficiency and finding best practices. DEA defines an efficiency envelope and all units inside the envelope are inefficient. Solving the linear programming equation not only gives us efficiency of different units but also establishes relative weights of each input and output variable.Using DEA, I was able to score efficiency of each branch and find the relation between different parameter. Using these metrics, I was able to do a root cause analysis for branch inefficiency and establish branch best practices.

What do think of this technique? Do you think this provides solution to any problem you face? Are there any other techniques you use to find efficiency of different business units? Are you able to tackle the linearity assumption with this technique? Do let us know your thoughts in comments below.

If you like what you just read & want to continue your analytics learning, subscribe to our emails or like our facebook page.

Tavish Srivastava
Tavish Srivastava

Tavish Srivastava, co-founder and Chief Strategy Officer of Analytics Vidhya, is an IIT Madras graduate and a passionate data-science professional with 8+ years of diverse experience in markets including the US, India and Singapore, domains including Digital Acquisitions, Customer Servicing and Customer Management, and industry including Retail Banking, Credit Cards and Insurance. He is fascinated by the idea of artificial intelligence inspired by human intelligence and enjoys every discussion, theory or even movie related to this idea.

Free Courses

Generative AI 4.7

Generative AI - A Way of Life

Explore Generative AI for beginners: create text and images, use top AI tools, learn practical skills, and ethics.
Large Language Models 4.5

Getting Started with Large Language Models

Master Large Language Models (LLMs) with this course, offering clear guidance in NLP and model training made simple.
Prompt Engineering 4.6

Building LLM Applications using Prompt Engineering

This free course guides you on building LLM apps, mastering prompt engineering, and developing chatbots with enterprise data.
LlamaIndex 4.8

Improving Real World RAG Systems: Key Challenges & Practical Solutions

Explore practical solutions, advanced retrieval strategies, and agentic RAG systems to improve context, relevance, and accuracy in AI-driven applications.
RAG systems using LlamaIndex 4.7

Microsoft Excel: Formulas & Functions

Master MS Excel for data analysis with key formulas, functions, and LookUp tools in this comprehensive course.

Recommended Articles

Responses From Readers

Clear

Kim-Yen Gan
Kim-Yen Gan

Hi Tavish. I like this approach. It reminds me of a similar concept used in Economics for determining efficient frontiers. But what if I wanted to take this one step further and analyse more than 2 inputs. How would this method apply? As I understand, this method as explained in your article only includes 2 inputs which can be plotted on the X & Y axis. Is the a way to graphically present more than 2 inputs?

123

Tavish Srivastava
Tavish Srivastava

Kim, The method can be used to any number of input (say i) and any number of output (say o). The graphical representation is only illustrative of how method works and is restricted to two output. You can use the simplex formulation discussed in the article to handle both multiple inputs and multiple outputs. Hope this helps. Tavish

123
Anil Kumar Goyal
Anil Kumar Goyal

Very Good explanation. Just a question, here we are assuming that we have a limited number of resources (inputs) and then we are calculating efficiency on the basis of output generated. But on the other hand we can have unlimited resources and we have to achieve certain fixed targets. In that case how can we calculate the efficiency of input deployment??

123

Write for us

Write, captivate, and earn accolades and rewards for your work
  • Reach a Global Audience
  • Get Expert Feedback
  • Build Your Brand & Audience
  • Cash In on Your Knowledge
  • Join a Thriving Community
  • Level Up Your Data Science Game
imag

We use cookies essential for this site to function well. Please click to help us improve its usefulness with additional cookies. Learn about our use of cookies in our Privacy Policy & Cookies Policy.

Show details