Operations analytics case study (level : hard)

In previous few articles (beginner, intermediate and queuing theory), we have completed a variety of case studies used in operation analytics. One of which was based on assignment algorithm in call centers. Today’s case study will be similar but we will now look at a more broader level instead of individual caller assignment. We will formulate this problem in a similar fashion as we try a transportation algorithm. While solving this problem, we will try multiple well known solutions to the transportation problem.

Operation Analytics and Investigating Metric Spike Case study

You own a call center with 1000 resources. Each of these resources have gone through a different set of trainings. These training combinations are A,B,C,D,E and F. For instance set A is the population who have gone through training 1,2,3,4,5 and 6. Similarly, set B has gone through some other set of trainings. The distribution of these callers are

A : 200

B : 200

C : 100

D : 100

E : 250

F : 150

Also, the calls you get on a daily basis have different types of queries. This can again be classified into 4 categories. Let’s call them X,Y,Z and W. Each of these category can be identified through an IVR and you can try to allot any caller to these customers. On a daily basis you get following distribution of calls :

X : 20%

Y : 30%

Z :  15%

W : 35%

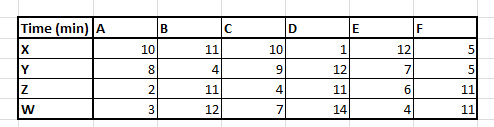
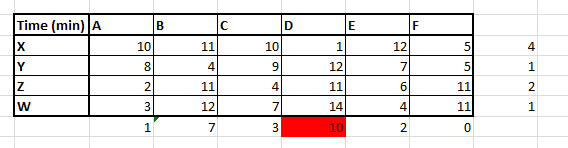
The number of calls might vary with days but remains almost constant at this ratio. With every set of trainings, you get a different type of skill set which enables a caller to resolve varied type of calls in different time. For instance, a set A agent can resolve a call X in 10 minutes. Following is a grid, which you can refer to check the resolution time for each combination :

Here is the catch! Your objective is to complete the work of all the callers in the least aggregate time. This will allow you to train them on different skills and therefore decrease the resolution time dynamically. Ultimately, you want a dynamic system which can do such an allocation on real time. However, for now you need to make the assignment so that you minimize the total time taken by all callers combined.

Kick Start the process

As of now, the problem is open ended till you assume the actual inflow of calls to a certain number. To simplify things, let’s assume that we have a balanced transportation problem in hand. Following is the distribution of calls :

X : 200 calls

Y : 300 calls

Z : 150 calls

W : 350 calls

Total calls : 1000 calls

Hence, the number of agents and calls are exactly equal. Even if the total number of calls increase, our current solution will still be valid as the ratio holds true.

Introduction to transportation problem

This is a classic transportation problem where the time is just a substitute of cost. Here, we try to minimize the total cost by making the right set of assignments. We can either solve it through a simplex or a tabular solution. Transportation problems are generally solved in two steps :

1. Identifying a basic feasible solution
2. Finding the optimal solution

For this article, my focus will be to complete the first step. I will leave the second step for the reader and based on the response on this article, will publish the second part as well if required.

Identifying a basic feasible solution can be done through 3 approaches :

1. North west corner rule (simplest of all)
2. Minimum cost method
3. Penalty cost method

North west corner rule

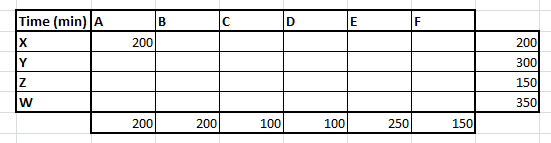
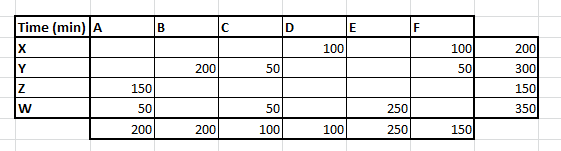
The process is very simple. We just assign the maximum possible values on the north west corner till we exhaust all the callers. We start as follows :

Here we were able to make this assignment because both supply and demand is 200. However, we make an assignment of a value which is the minimum of two, which coincidentally is the same here. Now we have exhausted both the first row and first column. Hence we move to the cell (B,Y) and make the next assignment. Sequentially we make all the possible assignments.

Now we calculate the total time which in this case comes out as 7550 minutes. To simply evaluate the results , we assign all A’s for X type of calls. We will divert around 33% of Y type calls to C type agents and 66% to B type agents & so on. This is generally the least optimal solution and we can get better results by the rest two methods.

Minimum cost method

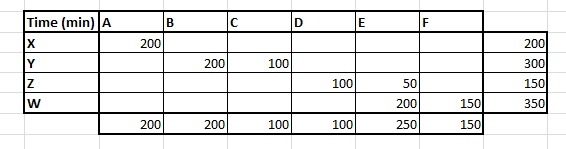
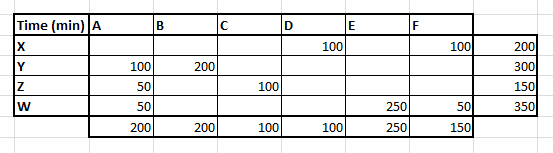
This method is slightly evolved version of the last one. Here we simply try finding out the smallest time which for a combination of caller-customer that are available. For instance, if we look at the entire cost matrix, we find the minimum time is for X customer being attended for caller D, hence we make the maximum assignment at this combination.

Finally we arrive at the following assignments :

The total time for this assignment now reduces to 3900 minutes which is almost a 50% reduction on the overall time.

Penalty cost method

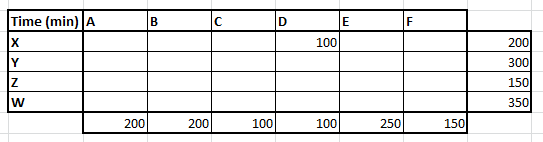
This is an even more evolved version of initial assignment procedure. Here we start with calculating the difference between the minimum and the 2nd minimum time for each row and column. This is basically the cost of not making an assignment in the current iteration. Following is our penalty cost table :

As we see the penalty cost is maximum for the caller types D. And we need to immediately assign the maximum value to caller D. Once done, we again recalculate all the penalty costs and move on with the assignment. Finally, following are the assignments

The total cost here is 4400, which is not better the last method. However, there is no guarantee of which algorithm wins in any iteration. It completely depends on the chances you break the tie in favor of lowering the cost or in opposite direction.

Thinkpot

Beyond this step, we now start our journey of optimization. This can again be done by multiple algorithms, namely – Stepping stone, MODI etc. However, you can progress on the simplex optimization to get the final solution. Once you have the final solution to this problem, mention the methodology and the final answer in the comment box below.

End Notes

Transportation problem is used widely in operation research but very rarely used in analytics industry. However, I have seen enormous number of opportunities which can be converted into such transportation problems. My motive of this article was to make you realize that how powerful these operation research tools can be, if we convert our problem in hand into such objective functions. Also do mention in the comment box below, if you would like me to further kill the problem of optimizing such transportation problem with the algorithms I have mentioned above.

Did you like reading this article ?  Do share your experience / suggestions in the comments section below. I’d love to know your

You can test your skills and knowledge. Check out Live Competitions and compete with best Data Scientists from all over the world.

Tavish Srivastava

Tavish Srivastava, co-founder and Chief Strategy Officer of Analytics Vidhya, is an IIT Madras graduate and a passionate data-science professional with 8+ years of diverse experience in markets including the US, India and Singapore, domains including Digital Acquisitions, Customer Servicing and Customer Management, and industry including Retail Banking, Credit Cards and Insurance. He is fascinated by the idea of artificial intelligence inspired by human intelligence and enjoys every discussion, theory or even movie related to this idea.