Interview Prep
Career
GenAI
Prompt Engg
ChatGPT
LLM
Langchain
RAG
AI Agents
Machine Learning
Deep Learning
GenAI Tools
LLMOps
Python
NLP
SQL
AIML Projects

Reading list

Machine Learning Basics for a Newbie
6 Steps of Machine learning Lifecycle Introduction to Predictive Modeling
Introduction to Exploratory Data Analysis & Data Insights Descriptive Statistics Inferential Statistics How to Understand Population Distributions?
Reading Data Files into Python Different Variable Datatypes
Probability for Data Science Basic Concepts of Probability Axioms of Probability Conditional Probability
Central Tendencies for Continuous Variables Spread of Data KDE plots for Continuous Variable Overview of Distribution for Continuous variables Normal Distribution Skewed Distribution Skeweness and Kurtosis Distribution for Continuous Variable
Central Tendencies for Categorical Variables Understanding Discrete Distributions Performing EDA on Categorical Variables
Dealing with Missing Values Understanding Outliers Identifying Outliers in Data Outlier Detection in Python Outliers Detection Using IQR, Z-score, LOF and DBSCAN
Sample and Population Central Limit Theorem Confidence Interval and Margin of Error
Bivariate Analysis Introduction
Covariance Pearson Correlation Spearman's Correlation & Kendall's Tau Correlation versus Causation Tabular and Graphical methods for Bivariate Analysis Performing Bivariate Analysis on Continuous-Continuous Variables
Tabular and Graphical methods for Continuous-Categorical Variables Introduction to Hypothesis Testing P-value Two sample Z-test T-test T-test vs Z-test Performing Bivariate Analysis on Continuous-Catagorical variables
Chi-Squares Test Bivariate Analysis on Categorical Categorical Variables
Multivariate Analysis A Comprehensive Guide to Data Exploration The Data Science behind IPL
Supervised Learning vs Unsupervised Learning Reinforcement Learning Generative and Descriminative Models Parametric and Non Parametric model
Machine Learning Pipeline Preparing Dataset Build a Benchmark Model: Regression Build a Benchmark Model: Classification
Evaluation Metrics for Machine Learning Everyone should know Confusion Matrix Accuracy Precision and Recall AUC-ROC Log Loss R2 and Adjusted R2
Dealing with Missing Values Replacing Missing Values Imputing Missing Values in Data Working with Categorical Variables Working with Outliers Preprocessing Data for Model Building
Understanding Cost Function Understanding Gradient Descent Math Behind Gradient Descent Assumptions of Linear Regression Implement Linear Regression from Scratch Train Linear Regression in Python Implementing Linear Regression in R Diagnosing Residual Plots in Linear Regression Models Generalized Linear Models Introduction to Logistic Regression Odds Ratio Implementing Logistic Regression from Scratch Introduction to Scikit-learn in Python Train Logistic Regression in python Multiclass using Logistic Regression How to use Multinomial and Ordinal Logistic Regression in R ? Challenges with Linear Regression Introduction to Regularisation Implementing Regularisation Ridge Regression Lasso Regression
Introduction to K Nearest Neighbours Determining the Right Value of K in KNN Implement KNN from Scratch Implement KNN in Python
Bias Variance Tradeoff Introduction to Overfitting and Underfitting Visualizing Overfitting and Underfitting Selecting the Right Model What is Validation? Hold-Out Validation Understanding K Fold Cross Validation
Introduction to Feature Selection Feature Selection Algorithms Missing Value Ratio Low Variance Filter High Correlation Filter Backward Feature Elimination Forward Feature Selection Implement Feature Selection in Python Implement Feature Selection in R
Introduction to Decision Tree Purity in Decision Tree Terminologies Related to Decision Tree How to Select Best Split Point in Decision Tree? Chi-Squares Information Gain Reduction in Variance Optimizing Performance of Decision Tree Train Decision Tree using Scikit Learn Pruning of Decision Trees
Introduction to Feature Engineering Feature Transformation Feature Scaling Feature Engineering Frequency Encoding Automated Feature Engineering: Feature Tools
Introduction to Naive Bayes Conditional Probability and Bayes Theorem Introduction to Bayesian Adjustment Rating: The Incredible Concept Behind Online Ratings! Working of Naive Bayes Math behind Naive Bayes Types of Naive Bayes Implementation of Naive Bayes
Understanding how to solve Multiclass and Multilabled Classification Problem Evaluation Metrics: Multi Class Classification
Introduction to Ensemble Techniques Basic Ensemble Techniques Implementing Basic Ensemble Techniques Finding Optimal Weights of Ensemble Learner using Neural Network Why Ensemble Models Work well?
Introduction to Stacking Implementing Stacking Variants of Stacking Implementing Variants of Stacking Introduction to Blending Bootstrap Sampling Introduction to Random Sampling Hyper-parameters of Random Forest Implementing Random Forest Out-of-Bag (OOB) Score in the Random Forest IPL Team Win Prediction Project Using Machine Learning Introduction to Boosting Gradient Boosting Algorithm Math behind GBM Implementing GBM in python Regularized Greedy Forests Extreme Gradient Boosting Implementing XGBM in python Tuning Hyperparameters of XGBoost in Python Implement XGBM in R/H2O Adaptive Boosting Implementing Adaptive Boosing LightGBM Implementing LightGBM in Python Catboost Implementing Catboost in Python
Different Hyperparameter Tuning methods Implementing Different Hyperparameter Tuning methods GridsearchCV RandomizedsearchCV Bayesian Optimization for Hyperparameter Tuning Hyperopt
Understanding SVM Algorithm SVM Kernels In-depth Intuition and Practical Implementation SVM Kernel Tricks Kernels and Hyperparameters in SVM Implementing SVM from Scratch in Python and R
Introduction to Principal Component Analysis Steps to Perform Principal Compound Analysis Computation of Covariance Matrix Finding Eigenvectors and Eigenvalues Implementing PCA in python Visualizing PCA A Brief Introduction to Linear Discriminant Analysis Introduction to Factor Analysis
Introduction to Clustering Applications of Clustering Evaluation Metrics for Clustering Understanding K-Means Implementation of K-Means in Python Implementation of K-Means in R Choosing Right Value for K Profiling Market Segments using K-Means Clustering Hierarchical Clustering Implementation of Hierarchial Clustering DBSCAN Defining Similarity between clusters Build Better and Accurate Clusters with Gaussian Mixture Models
Understand Basics of Recommendation Engine with Case Study
8 Ways to Improve Accuracy of Machine Learning Models
Introduction to Dask Working with CuML
Introduction to Machine Learning Interpretability Framework and Interpretable Models model Agnostic Methods for Interpretability Implementing Interpretable Model Understanding SHAP Out-of-Core ML Introduction to Interpretable Machine Learning Models Model Agnostic Methods for Interpretability Game Theory & Shapley Values
Introduction to Machine Learning Interpretability Framework and Interpretable Models model Agnostic Methods for Interpretability Implementing Interpretable Model Understanding SHAP Out-of-Core ML Introduction to Interpretable Machine Learning Models Model Agnostic Methods for Interpretability Game Theory & Shapley Values
Introduction to AutoML Implementation of MLBox Introduction to PyCaret TPOT Auto-Sklearn EvalML
Pickle and Joblib Introduction to Model Deployment
Deploying Machine Learning Model using Streamlit Deploying ML Models in Docker Deploy Using Streamlit Deploy on Heroku Deploy Using Netlify Introduction to Amazon Sagemaker Setting up Amazon SageMaker Using SageMaker Endpoint to Generate Inference Deploy on Microsoft Azure Cloud Introduction to Flask for Model Deploying ML model using Flask
Model Deployment in Android Model Deployment in Iphone

Framework to build logistic regression model in a rare event population

Tavish Srivastava
Tavish Srivastava Last Updated : 25 Jun, 2020
4 min read

Only 531 out of a population of 50,431 customer closed their saving account in a year, but the dollar value lost because of such closures was more than $ 5 Million.

The best way to arrest these attrition was by predicting the propensity of attrition for individual customer and then pitch retention offers to these identified customers. This was  a typical case of modeling in a rare event population. This kind of problems are also very common in Health care analytics.

In such analysis, there are two challenges :

  1. Accurate prediction is difficult because of small sample bias.
  2. The accuracy of prediction need to be extremely high to make an implementable strategy. This is because high number of false positive, unnecessarily burdens the retention budgets.

modeling rare events

We can find number of statistical papers on this specific problem. This article will collect the best practices and layout the step by step process to make a logistic regression model in a rare event population.

[stextbox id=”section”]Why not simply make a logistic regression model on the population? [/stextbox]

The problem basically is that maximum likelihood estimation of the logistic model is well-known to suffer from small-sample bias. And the degree of bias is strongly dependent on the number of cases in the less frequent of the two categories. Try estimating the degree of bias in each of the following samples:

A. 20 events in a sample size of 1000 (Response rate : 2%)

B. 180 events in a sample size of 10000 (Response rate : 1.8%)

C.  990 events in a sample size of 1000 (Response rate : 99%)

Try not to see the answer below before you have your answer ready.

The correct answer here is C > A > B . C will suffer with the problem of small-sample bias most. Confused? Did we not say this problem exist in cases where events are too low? The problem is not specifically the rarity of events, but rather the possibility of a small number of cases on the rarer of the two outcomes. Why “A>B”? Its simply because of the population size. Even though the response rate in B is lesser than A, A struggles with the problem more than B. Hence, smaller the sample size ,higher is the risk of small sample bias.

[stextbox id=”section”] What is the solution in such problems? [/stextbox]

The solution in such problems is slightly longer than a normal logistic regression model. In such cases, we make a biased sample to increase the proportion of events. Now, we run logistic regression on the sample created. Once we have the final Logit equation, we transform the equation to fit the entire population.

biased

[stextbox id=”section”]Case study:  [/stextbox]

Let’s consider the case in hand and walk through the step by step process. We have a population of 50,431 customers out of which 531 attrite in 12 months. We need to predict the probability of attrition, minimizing the false positives.

Step 1 :Select a biased sample

Total number of non attritors in the population is 49,900. We plan to take a sample of 1000 customers.  As a thumb rule, we select 25% of the sample size as the responders. Hence, we select 250 customers out of the 531 attriting customers. And rest 750 come from the 49,900 base. This sample of 1000 customers is a biased sample we will consider for our analysis.

Step 2 : Develop the regression model

We now build a logistic regression model on the biased sample selected. We make sure that all the assumptions of the logistic regression are met and we get a reasonable lift because the lift tends to decrease after the transformations.

Step 3 : Overlay equation on the population:

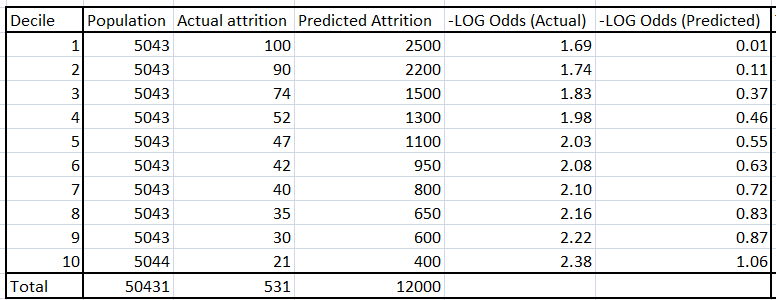
Using the equation found in step 2, get the number of attritors in each decile of the overall population. In the table below, -Log odds (Predicted) directly comes from the regression equation. Using this function, one can find the Predicted attrition for each decile.

wo_trans

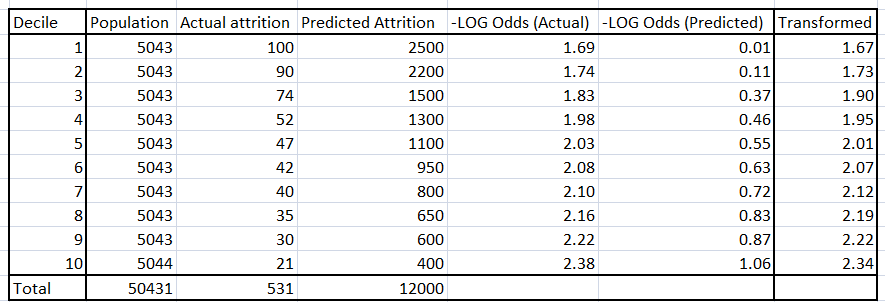
 Step 4: Solve for intercept and slope transformation

Using the actual and the predicted decile value of the log odds, we find the slope and the intercept required to transform the equation of the sample to the equation of the population. This equation is given by,

{- Log odds (actual)} = slope * {-Log odds(predicted)} + Intercept

Find the slope and intercept using the 10 data-points, each corresponding to each decile.

transformation

In this case slope is 0.63 and the intercept is 1.66 .

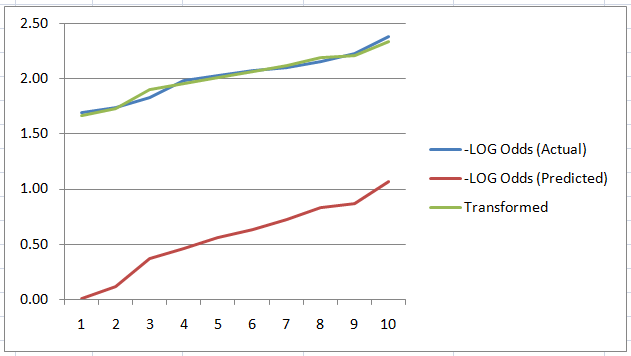
logit

As seen from the above figure, the actual and the transformed logit curve for each decile is much closer compared to the predicted curve.

Step 5: Validate the equation on out of time sample :

Once we reach a final equation of the logit function, we now validate the same on out of time samples. For the case in hand, we take a different cohort and compile the lift chart. If the model holds on out of time as well, we are good to go.

[stextbox id=”section”]End Notes:  [/stextbox]

Did you find the article useful? Share with us any other techniques you incorporate while solving a rare event problem.  Do let us know your thoughts about this article in the box below.

If you like what you just read & want to continue your analytics learning, subscribe to our emails or like our facebook page.

Tavish Srivastava
Tavish Srivastava

Tavish Srivastava, co-founder and Chief Strategy Officer of Analytics Vidhya, is an IIT Madras graduate and a passionate data-science professional with 8+ years of diverse experience in markets including the US, India and Singapore, domains including Digital Acquisitions, Customer Servicing and Customer Management, and industry including Retail Banking, Credit Cards and Insurance. He is fascinated by the idea of artificial intelligence inspired by human intelligence and enjoys every discussion, theory or even movie related to this idea.

Free Courses

Generative AI 4.7

Generative AI - A Way of Life

Explore Generative AI for beginners: create text and images, use top AI tools, learn practical skills, and ethics.
Large Language Models 4.5

Getting Started with Large Language Models

Master Large Language Models (LLMs) with this course, offering clear guidance in NLP and model training made simple.
Prompt Engineering 4.6

Building LLM Applications using Prompt Engineering

This free course guides you on building LLM apps, mastering prompt engineering, and developing chatbots with enterprise data.
LlamaIndex 4.8

Improving Real World RAG Systems: Key Challenges & Practical Solutions

Explore practical solutions, advanced retrieval strategies, and agentic RAG systems to improve context, relevance, and accuracy in AI-driven applications.
RAG systems using LlamaIndex 4.7

Microsoft Excel: Formulas & Functions

Master MS Excel for data analysis with key formulas, functions, and LookUp tools in this comprehensive course.

Recommended Articles

Responses From Readers

Clear

dimalvov
dimalvov

Hello Tavish it is a nice post. I usually prefer to oversample the cases with such probability that would equalize the proportions in cases/controls though.

123

Tavish
Tavish

Over sampling is a must. It will really helpful if you share how do you translate the found equation on oversample to actual population. Tavish

123
saras
saras

Hello you say "Using the equation found in step 2," but there is no equation given. Can you give this equation please and explain how you get the values given in the table below part 3 ? I am working on a real life problem related to rare events in a children's hospital. I would like to your method to see if I can predict readmission. thanks. saras

123

Tavish Srivastava
Tavish Srivastava

Hi Saras, Equation found in step 2 is the equation you get after running the regression model o biased sample. Table 3 can be directly generated similar to one you make for finding the ks of model. Do let us know of this is still not clear. Tavish

123
Mark
Mark

Very good post. Thanks! I am not sure how did you calculate the transformed value and slop/intercept. Could you explain more? Mark

123

Tavish
Tavish

Mark, What we are trying to do here is transform the found logistic equation using the actual unbiased sample. The first thing you need to do is to sort your data-points in the order of predicted attrition. Now decile your population and find the logit for actual attrition and predicted attrition. Now using the equation "{- Log odds (actual)} = slope * {-Log odds(predicted)} + Intercept " find the slope and intercept adjustment factor. Hope this helps. Tavish

123

Write for us

Write, captivate, and earn accolades and rewards for your work
  • Reach a Global Audience
  • Get Expert Feedback
  • Build Your Brand & Audience
  • Cash In on Your Knowledge
  • Join a Thriving Community
  • Level Up Your Data Science Game
imag

We use cookies essential for this site to function well. Please click to help us improve its usefulness with additional cookies. Learn about our use of cookies in our Privacy Policy & Cookies Policy.

Show details