Introduction
We have several machine learning algorithms at our disposal for model building. Doing data based prediction is now easier like never before. Whether it is a regression or classification problem, one can effortlessly achieve a reasonably high accuracy using a suitable algorithm. But, this is not the case everytime. Classification problems can sometimes get a bit tricky.
ML algorithms tend to tremble when faced with imbalanced classification data sets. Moreover, they result in biased predictions and misleading accuracies. But, why does it happen ? What factors deteriorate their performance ?
The answer is simple. With imbalanced data sets, an algorithm doesn’t get the necessary information about the minority class to make an accurate prediction. Hence, it is desirable to use ML algorithms with balanced data sets, especially in the realm of data science. When building a predictive model, it’s crucial to address the challenge of imbalanced data sets effectively. Then, how should we deal with imbalanced data sets? The methods are simple but tricky as described in this article.
In this tutorial, I’ve shared the important things you need to know to tackle imbalanced classification in R problems. In particular, I’ve kept my focus on imbalance in binary classification problems. As usual, I’ve kept the explanation simple and informative. Towards the end, I’ve provided a practical view of dealing with such data sets in R with ROSE package.

Table of contents
What is Imbalanced Classification ?
Imbalanced classification is a supervised learning problem where one class outnumbers other class by a large proportion. This problem is faced more frequently in binary classification problems than multi-level classification problems.
The term imbalanced refers to the disparity encountered in the dependent (response) variable. Therefore, an imbalanced classification problem is one in which the dependent variable exhibits an unequal distribution of classes. This means that the training set may contain significantly more instances of one class compared to others, leading to challenges in accurately predicting minority class instances. Similarly, when evaluating the model’s performance, it’s essential to consider its effectiveness across both the training set and the test set, ensuring robustness in handling imbalanced data distributions. In other words, a dataset that exhibits an unequal distribution between its classes is considered imbalanced.
Example of Imbalanced Classification in R
Consider a dataset with 100,000 observations, comprised of candidates who have applied for an internship at Harvard. Harvard, renowned for its exceptionally low acceptance rate, poses a formidable challenge for applicants. The dependent variable in this dataset indicates whether a candidate has been shortlisted (1) or not shortlisted (0). Upon analysis, it becomes evident that approximately 98% of candidates did not secure a spot, while a mere 2% were fortunate enough to receive an invitation. This scenario exemplifies a classic case of imbalanced classification, where techniques such as logistic regression can offer insights into predicting the likelihood of shortlisting based on various candidate attributes.
In real life, situations where imbalanced classes occur are quite common. Yes! For better understanding, here are some real-life examples. Please note that the degree of imbalance varies per situation.
- An automated inspection machine which detect products coming off manufacturing assembly line may find number of defective products significantly lower than non defective products.
- A test done to detect cancer in residents of a chosen area may find the number of cancer affected people significantly less than unaffected people.
- In credit card fraud detection, fraudulent transactions will be much lower than legitimate transactions.
- A manufacturing operating under six sigma principle may encounter 10 in a million defected products.
There are many more real life situations which result in imbalanced data set. Now you see, the chances of obtaining an imbalanced data is quite high. Hence, it’s important to learn to deal with such problems for every analyst.
Also Read: A Complete Tutorial to learn Data Science in R from Scratch
Why do Standard ML Algorithms Struggle with Accuracy on Imbalanced Data?
This is an interesting experiment to do. Try it! This way you will understand the importance of learning the ways to restructure imbalanced data. I’ve shown this in the practical section below.
Below are the reasons which leads to reduction in accuracy of ML algorithms on imbalanced data sets:
- ML algorithms struggle with accuracy because of the unequal distribution in dependent variable.
- This causes the performance of existing classifiers to get biased towards majority class.
- The algorithms are accuracy driven i.e. they aim to minimize the overall error to which the minority class contributes very little.
- ML algorithms assume that the data set has balanced class distributions.
- They also assume that errors obtained from different classes have same cost (explained below in detail).
What are the Methods to Deal with Imbalanced Datasets ?
The methods are widely known as ‘Sampling Methods’. Generally, these methods aim to modify an imbalanced data into balanced distribution using some mechanism. The modification occurs by altering the size of original data set and provide the same proportion of balance.
These methods have acquired higher importance, especially when dealing with a new dataset, after numerous research studies have demonstrated that balanced data yields superior classification performance compared to an imbalanced dataset. Therefore, it’s crucial to familiarize oneself with them.
Below are the methods used to treat imbalanced datasets:
- Undersampling
- Oversampling
- Synthetic Data Generation
- Cost Sensitive Learning
Let’s understand them one by one.
Undersampling
This method works with majority class. It reduces the number of observations from majority class to make the data set balanced. This method is best to use when the data set is huge and reducing the number of training samples helps to improve run time and storage troubles.
Undersampling methods are of 2 types: Random and Informative.
Random undersampling method randomly chooses observations from majority class which are eliminated until the data set gets balanced. Informative undersampling follows a pre-specified selection criterion to remove the observations from majority class.
Within informative undersampling, EasyEnsemble and BalanceCascade algorithms are known to produce good results. These algorithms are easy to understand and straightforward too.
EasyEnsemble: At first, it extracts several subsets of independent sample (with replacement) from majority class. Then, it develops multiple classifiers based on combination of each subset with minority class. As you see, it works just like a unsupervised learning algorithm.
BalanceCascade: It takes a supervised learning approach where it develops an ensemble of classifier and systematically selects which majority class to ensemble.
Do you see any problem with undersampling methods? Apparently, removing observations may cause the training data to lose important information pertaining to majority class.
Oversampling
This method works with minority class. It replicates the observations from minority class to balance the data. It is also known as upsampling. Similar to undersampling, this method also can be divided into two types: Random Oversampling and Informative Oversampling.
Random oversampling balances the data by randomly oversampling the minority class. Informative oversampling uses a pre-specified criterion and synthetically generates minority class observations.
An advantage of using this method is that it leads to no information loss. The disadvantage of using this method is that, since oversampling simply adds replicated observations in original data set, it ends up adding multiple observations of several types, thus leading to overfitting. Although, the training accuracy of such data set will be high, but the accuracy on unseen data will be worse.
Synthetic Data Generation
In simple words, instead of replicating and adding the observations from the minority class, it overcome imbalances by generates artificial data. It is also a type of oversampling technique.
In regards to synthetic data generation, synthetic minority oversampling technique (SMOTE) is a powerful and widely used method. SMOTE algorithm creates artificial data based on feature space (rather than data space) similarities from minority samples. We can also say, it generates a random set of minority class observations to shift the classifier learning bias towards minority class.
To generate artificial data, it uses bootstrapping and k-nearest neighbors. Precisely, it works this way:
- Take the difference between the feature vector (sample) under consideration and its nearest neighbor.
- Multiply this difference by a random number between 0 and 1
- Add it to the feature vector under consideration
- This causes the selection of a random point along the line segment between two specific features
R has a very well defined package which incorporates this techniques. We’ll look at it in practical section below.
Cost Sensitive Learning (CSL)
It is another commonly used method to handle classification problems with imbalanced data. It’s an interesting method. In simple words, this method evaluates the cost associated with misclassifying observations.
It does not create balanced data distribution. Instead, it highlights the imbalanced learning problem by using cost matrices which describes the cost for misclassification in a particular scenario. Recent researches have shown that cost sensitive learning have many a times outperformed sampling methods. Therefore, this method provides likely alternative to sampling methods.
Let’s understand it using an interesting example: A data set of passengers in given. We are interested to know if a person has bomb. The data set contains all the necessary information. A person carrying bomb is labeled as positive class. And, a person not carrying a bomb in labeled as negative class. The problem is to identify which class a person belongs to. Now, understand the cost matrix.
There in no cost associated with identifying a person with bomb as positive and a person without negative. Right ? But, the cost associated with identifying a person with bomb as negative (False Negative) is much more dangerous than identifying a person without bomb as positive (False Positive).
Cost Matrix
Cost Matrix is similar of confusion matrix. It’s just, we are here more concerned about false positives and false negatives (shown below). There is no cost penalty associated with True Positive and True Negatives as they are correctly identified.
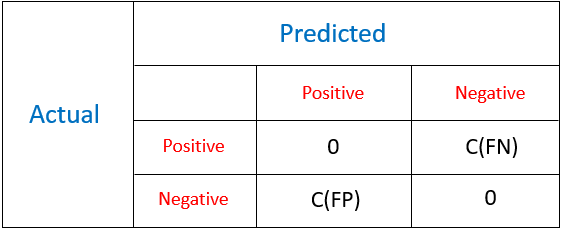
Cost Matrix
The goal of this method is to choose a classifier with lowest total cost.
Total Cost = C(FN)xFN + C(FP)xFPwhere,
- FN is the number of positive observations wrongly predicted
- FP is the number of negative examples wrongly predicted
- C(FN) and C(FP) corresponds to the costs associated with False Negative and False Positive respectively. Remember, C(FN) > C(FP).
There are other advanced methods as well for balancing imbalanced data sets. These are Cluster based sampling, adaptive synthetic sampling, border line SMOTE, SMOTEboost, DataBoost – IM, kernel based methods and many more. The basic working on these algorithm is almost similar as explained above. There are more intuitive methods which you can try for improved predictions:
- Using clustering, divide the majority class into K distinct cluster. There should be no overlap of observations among these clusters. Train each of these cluster with all observations from minority class. Finally, average your final prediction.
- Collect more data. Aim for more data having higher proportion of minority class. Otherwise, adding more data will not improve the proportion of class imbalance.
Which Performance Metrics to Use to Evaluate Accuracy ?
Choosing a performance metric is a critical aspect of working with imbalanced data. Most classification algorithms calculate accuracy based on the percentage of observations correctly classified. With imbalanced data, the results are high deceiving since minority classes hold minimum effect on overall accuracy.

The difference between confusion matrix and cost matrix is that, cost matrix provides information only about the misclassification cost, whereas confusion matrix describes the entire set of possibilities using TP, TN, FP, FN. In a cost matrix, the diagonal elements are zero. The most frequently used metrics are Accuracy & Error Rate.
Accuracy: (TP + TN)/(TP+TN+FP+FN)Error Rate = 1 - Accuracy = (FP+FN)/(TP+TN+FP+FN)As mentioned above, these metrics may provide deceiving results and are highly sensitive to changes in data. Further, various metrics can be derived from confusion matrix.
Better Measure to Calculate Accuracy
The resulting metrics provide a better measure to calculate accuracy while working on a imbalanced data set:
Precision
It is a measure of correctness achieved in positive prediction i.e. of observations labeled as positive, how many are actually labeled positive.
Precision = TP / (TP + FP)Recall
It is a measure of actual observations which are labeled (predicted) correctly i.e. how many observations of positive class are labeled correctly. It is also known as ‘Sensitivity’.
Recall = TP / (TP + FN)F measure
It combines precision and recall as a measure of effectiveness of classification in terms of ratio of weighted importance on either recall or precision as determined by β coefficient.
F measure = ((1 + β)² × Recall × Precision) / ( β² × Recall + Precision )
β is usually taken as 1.
Though, these methods are better than accuracy and error metric, but still ineffective in answering the important questions on classification. For example: precision does not tell us about negative prediction accuracy. Recall is more interesting in knowing actual positives. This suggest, we can still have a better metric to cater to our accuracy needs.
ROC
Fortunately, we have a ROC (Receiver Operating Characteristics) curve to measure the accuracy of a classification prediction. It’s the most widely used evaluation metric. ROC Curve is formed by plotting TP rate (Sensitivity) and FP rate (Specificity).
Specificity = TN / (TN + FP)Any point on ROC graph, corresponds to the performance of a single classifier on a given distribution. It is useful because if provides a visual representation of benefits (TP) and costs (FP) of a classification data. The larger the area under ROC curve, higher will be the accuracy.
There may be situations when ROC fails to deliver trustworthy performance. It has few shortcomings such as:
- It may provide overly optimistic performance results of highly skewed data.
- It does not provide confidence interval on classifier’s performance
- It fails to infer the significance of different classifier performance.
As alternative methods, we can use other visual representation metrics include PR curve, cost curves as well. Specifically, cost curves are known to possess the ability to describe a classifier’s performance over varying misclassification costs and class distributions in a visual format. In more than 90% instances, ROC curve is known to perform quite well.
Imbalanced Classification in R
Till here, we’ve learnt about some essential theoretical aspects of imbalanced classification. It’s time to learn to implement these techniques practically. In R, packages such as ROSE and DMwR helps us to perform sampling strategies quickly. We’ll work on a problem of binary classification.
ROSE (Random Over Sampling Examples) package helps us to generate artificial data based on sampling methods and smoothed bootstrap approach. This package has well defined accuracy functions to do the tasks quickly.
Let’s get started
#set path
> path <- "C:/Users/manish/desktop/Data/March 2016"
#set working directory
> setwd(path)
#install packages
> install.packages("ROSE")
> library(ROSE)Loading ROSE in R
The package ROSE comes with an inbuilt imbalanced data set named as hacide. It comprises of two files: hacide.train and hacide.test. Let’s load it in R environment:
> data(hacide)
> str(hacide.train)
'data.frame': 1000 obs. of 3 variables:
$ cls: Factor w/ 2 levels "0","1": 1 1 1 1 1 1 1 1 1 1 ...
$ x1 : num 0.2008 0.0166 0.2287 0.1264 0.6008 ...
$ x2 : num 0.678 1.5766 -0.5595 -0.0938 -0.2984 ...Check the Severity of Imbalance Dataset
As you can see, the data set contains 3 variable of 1000 observations. cls is the response variable. x1 and x2 are dependent variables. Let’s check the severity of imbalance in this data set:
#check table
table(hacide.train$cls)
0 1
980 20
#check classes distribution
prop.table(table(hacide.train$cls))
0 1
0.98 0.02Building a Model
As we see, this data set contains only 2% of positive cases and 98% of negative cases. This is a severely imbalanced data set. So, how badly can this affect our prediction accuracy ? Let’s build a model on this data. I’ll be using decision tree algorithm for modeling purpose.
> library(rpart)
> treeimb <- rpart(cls ~ ., data = hacide.train)
> pred.treeimb <- predict(treeimb, newdata = hacide.test)Checking Accuracy
Let’s check the accuracy of this prediction. To check accuracy, ROSE package has a function names accuracy.meas, it computes important metrics such as precision, recall & F measure.
> accuracy.meas(hacide.test$cls, pred.treeimb[,2])
Call:
accuracy.meas(response = hacide.test$cls, predicted = pred.treeimb[, 2])
Examples are labelled as positive when predicted is greater than 0.5
precision: 1.000
recall: 0.200
F: 0.167These metrics provide an interesting interpretation. With threshold value as 0.5, Precision = 1 says there are no false positives. Recall = 0.20 is very much low and indicates that we have higher number of false negatives. Threshold values can be altered also. F = 0.167 is also low and suggests weak accuracy of this model.
Final Accuracy Check using ROC Curve
We’ll check the final accuracy of this model using ROC curve. This will give us a clear picture, if this model is worth. Using the function roc.curve available in this package:
> roc.curve(hacide.test$cls, pred.treeimb[,2], plotit = F)Area under the curve (AUC): 0.600
AUC = 0.60 is a terribly low score. Therefore, it is necessary to balanced data before applying a machine learning algorithm. In this case, the algorithm gets biased toward the majority class and fails to map minority class.
Using Sampling Techniques to Improve Accuracy
We’ll use the sampling techniques and try to improve this prediction accuracy. This package provides a function named ovun.sample which enables oversampling, undersampling in one go.
Let’s start with oversampling and balance the data.
#over sampling
> data_balanced_over <- ovun.sample(cls ~ ., data = hacide.train, method = "over",N = 1960)$data
> table(data_balanced_over$cls)
0 1
980 980In the code above, method over instructs the algorithm to perform over sampling. N refers to number of observations in the resulting balanced set. In this case, originally we had 980 negative observations. So, I instructed this line of code to over sample minority class until it reaches 980 and the total data set comprises of 1960 samples.
Performing Undersampling
Similarly, we can perform undersampling as well. Remember, undersampling is done without replacement.
> data_balanced_under <- ovun.sample(cls ~ ., data = hacide.train, method = "under", N = 40, seed = 1)$data> table(data_balanced_under$cls)0 1 20 20
Now the data set is balanced. But, you see that we’ve lost significant information from the sample. Let’s do both undersampling and oversampling on this imbalanced data. This can be achieved using method = “both“. In this case, the minority class is oversampled with replacement and majority class is undersampled without replacement.
> data_balanced_both <- ovun.sample(cls ~ ., data = hacide.train, method = "both", p=0.5, N=1000, seed = 1)$data
> table(data_balanced_both$cls)
0 1
520 480p refers to the probability of positive class in newly generated sample.
Generating Data using ROSE
The data generated from oversampling have expected amount of repeated observations. Data generated from undersampling is deprived of important information from the original data. This leads to inaccuracies in the resulting performance. To encounter these issues, ROSE helps us to generate data synthetically as well. The data generated using ROSE is considered to provide better estimate of original data.
> data.rose <- ROSE(cls ~ ., data = hacide.train, seed = 1)$data
> table(data.rose$cls)
0 1
520 480This generated data has size equal to the original data set (1000 observations). Now, we’ve balanced data sets using 4 techniques. Let’s compute the model using each data and evaluate its accuracy.
#build decision tree models
> tree.rose <- rpart(cls ~ ., data = data.rose)
> tree.over <- rpart(cls ~ ., data = data_balanced_over)
> tree.under <- rpart(cls ~ ., data = data_balanced_under)
> tree.both <- rpart(cls ~ ., data = data_balanced_both)
#make predictions on unseen data
> pred.tree.rose <- predict(tree.rose, newdata = hacide.test)
> pred.tree.over <- predict(tree.over, newdata = hacide.test)
> pred.tree.under <- predict(tree.under, newdata = hacide.test)
> pred.tree.both <- predict(tree.both, newdata = hacide.test)It’s time to evaluate the accuracy of respective predictions. Using inbuilt function roc.curve allows us to capture roc metric.
#AUC ROSE
> roc.curve(hacide.test$cls, pred.tree.rose[,2])
Area under the curve (AUC): 0.989
#AUC Oversampling
roc.curve(hacide.test$cls, pred.tree.over[,2])
Area under the curve (AUC): 0.798
#AUC Undersampling
roc.curve(hacide.test$cls, pred.tree.under[,2])
Area under the curve (AUC): 0.867
#AUC Both
roc.curve(hacide.test$cls, pred.tree.both[,2])
Area under the curve (AUC): 0.798Here is the resultant ROC curve where:
- Black color represents ROSE curve
- Red color represents oversampling curve
- Green color represents undersampling curve
- Blue color represents both sampling curve
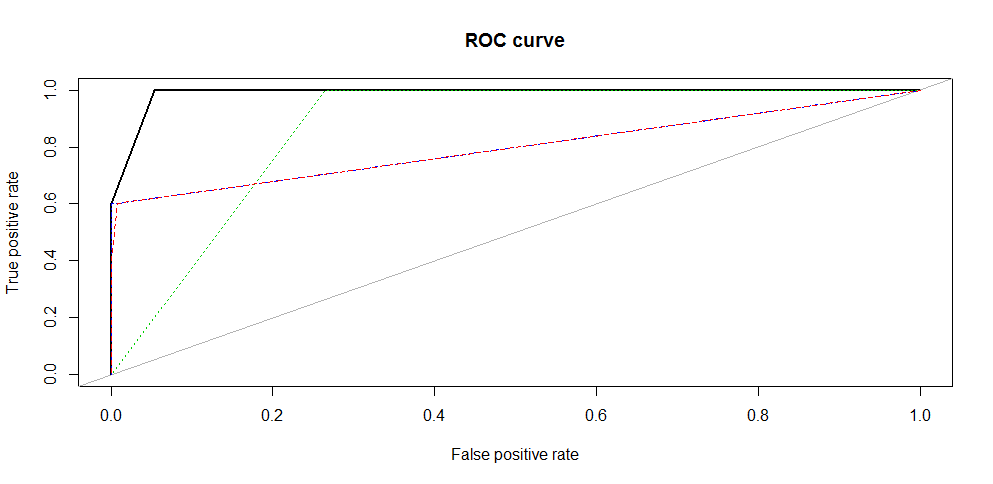
Hence, we get the highest accuracy from data obtained using ROSE algorithm. We see that the data generated using synthetic methods result in high accuracy as compared to sampling methods. This technique combined with a more robust algorithm (random forest, boosting) can lead to exceptionally high accuracy.
This package also provide us methods to check the model accuracy using holdout and bagging method. This helps us to ensure that our resultant predictions doesn’t suffer from high variance.
> ROSE.holdout <- ROSE.eval(cls ~ ., data = hacide.train, learner = rpart, method.assess = "holdout", extr.pred = function(obj)obj[,2], seed = 1)
> ROSE.holdout
Call:
ROSE.eval(formula = cls ~ ., data = hacide.train, learner = rpart,
extr.pred = function(obj) obj[, 2], method.assess = "holdout",
seed = 1)
Holdout estimate of auc: 0.985We see that our accuracy retains at ~ 0.98 and indicates that our predictors aren’t suffering from high variance. Similarly, you can use bootstrapping by setting method.assess to “BOOT”. The parameter extr.pred is a function which extracts the column of probabilities belonging to the positive class.
Conclusion
When faced with imbalanced classification in R, one might need to experiment with these methods to get the best suited sampling technique. In our case, we found that synthetic sampling technique outperformed the traditional oversampling and undersampling method. For better results, you can use advanced sampling methods which includes synthetic sampling with boosting methods.
In this article, I’ve discussed the important things one should know to deal with imbalanced data sets. For R users, dealing with such situations isn’t difficult since we are blessed with some powerful and awesome packages.
Did you find this article helpful ? Have you used these methods before? Do share your experience / suggestions in the comments section below.
o further enhance your skills in R and data science, consider enrolling in our AI/ML BlackBelt Plus program.
Frequently Asked Questions
A. In R, you can handle class imbalance by employing techniques such as oversampling, undersampling, or utilizing algorithmic approaches like cost-sensitive learning.
A. The three common methods are oversampling (increasing minority class samples), undersampling (decreasing majority class samples), and employing algorithms designed for imbalanced data.
A. Imbalanced datasets present challenges such as biased model performance, where the model may favor the majority class, leading to poor predictions for the minority class and potentially overlooking rare but significant patterns.
A. The challenge lies in effectively identifying and predicting minority class instances, as traditional algorithms often prioritize accuracy over sensitivity to the minority class, impacting overall model performance and decision-making.








Hi Manish, Great article.!!! Just a query...how do we arrive at the values for C(FP) & C(FN)?
This could either be based on domain knowledge or using the distribution of target data itself (say for every 5 instances in the data set 4 instances belong to class Y & 1 to class N then the cost of predicting a FalsePositive would be 4 times the cost of predicting a FalseNegative)
Nice Maniesh, Really get excellent information in both theory and practical side.
Here hacide.test$cls contains the target variable , but in general test data does not contains target . So what should we do ? I m getting this error : Error in accuracy.meas(y, pred.treeimb) : Response and predicted must have the same length. It cant be same since train response has diffrent length and pred.treeimb has diffrent length
Hello Rohit, In almost all Test data sets doesn't have dependent variable by default.. But we have to add that into test dataset. There are many ways to add variable into data set, But I'm suggesting you simplest way follow it test$dependent_variable<-" " I hope, it might helpful for you.
Good article, in real life most of time we will have imbalanced data set
Hi Manish, Happy to listen you love to help others, kindly suggest me book regarding R programming with statistical techniques.
I will be the annoying Python Person and ask, are there similar packages in Python? I searched without much luck..
There's a package available in python called [imbalanced-learn](https://github.com/scikit-learn-contrib/imbalanced-learn). You should check it out!
Perfect explanation!! Been trying to understand this topic since long, mostly during a logistic regression exercise of predicting customer churn...and finally! Just the necessary theory, coupled with a fantastic practical implementation. Great help
If we have unseen test set (ie, when we do not know the class labels of the target variable), how do we predict probabilities using the holdout approach? Can this algorithm be used to generate predicted probabilities for unseen data as well?
Hi Manish Thanks for the article. Is there a way to deal with imbalance when there are multiple classes
have you got the answer to your question ? if so then please help me.. I stuck in similar situation
"Error in rose.sampl(n, N, p, ind.majo, majoY, ind.mino, minoY, y, classy, : The current implementation of ROSE handles only continuous and categorical variables." Any clue besides the obvious why i would be getting this error even if my dependent is as in the example and my independent variables are continuous? Am i missing out something else? Kind regards and thank you in advance
Hi Manish, Its a great Article ...! I have A question on Sampling , the whole article is talking about reducing the bias in Dataset When the Dataset itself has unequal Classifiers, What's the point in pruning the samples which leads to equal/balanced Classifiers either by ROSE / OVUN /anyother package At this situation accuracy is high due to over fit....?. Please correct me if i am wrong
Please ignore over fit ... I wonder whether accuracy is valid...?
I work with extreme imbalanced dataset all the time. I used SMOTE , undersampling ,and the weight of the model . for example. c5.0 , xgboost Also, I need to tune the probability of the binary classification to get better accuracy. But, I found that ,for example, I use the 2014's data to build a good model (with 10-fold), but when I use the clean 2015's data to test ... then the overfittig problem comes ... . Are there anyone also meet this problem ? bty , I dont speak english ... I need google translator to help me ...
Sir, Can i know sir how you assign weight and how weighting works in RF. If you have some good tutorials or paper please refer me.
I have same problem too. Can anyone give solution for this problem? Hopefully there is. Thank you.
This is the most common problems faced by the researches in the Market research ( Imbalance data), So this article resolves the same .. Superb stuff
I afraid you have the wrong F measure, It should be beta square,rather than (1+beta) square
Hi Manish, if three someting wrong wrong with the F measure?we learn it is (1+beta's square),rather than the square of (1+beta)
Very well explained! Can the same technique be used for time series data too.
I am having a data set imbalance situation with 99% negative and 1% positive cases. SMOTE did not give me satisfactory result. Looking at boosting techniques now. Please discuss if any of you have faced such a situation.
Hi! Always we need balance our data set the best split is 50/50? Or we can balance in 70/30 for example? Thanks
Any function in any package which does the same task as accuracy.meas of ROSE package in R ? I am solving classification problem.
Thanks a megaton!!! You saved me a lot of work and investigation!!! I couldn't get the same accuracy on R as the one I was getting with Weka in Java, I thought it was an issue of R. Now I'm getting even better accuracy than in Java!!! :-)
Hi Manish There is error in Specificity formula. You have mentioned Specificity = TN / (TN + FP) where as Specificity = FP / (FP + TN)
Specificity is False positive Rate . But Formula mentioned True Negative Rate.. I am confused in these two terms. Could you please clear this doubt ?
Thank you so much Manish! Very clear and precise
Hi, everyone, how to assign weight to variable in random forest?
Very nicely explained .impressed with explanation and examples :)
Hi, I am still very new to R. Could anyone please explain to me why do we use [,2] in "accuracy.meas(hacide.test$cls, pred.treeimb[,2])" ?
As others have already posted, this is a fine article with intuitive explanations. Thanks!
Thanks a lot Manish! This is clearly understood article for imbalanced data.
very good explanation!!! i have one doubt, if i have more than two classes how can i extend this?
Great article/tutorial. I am following your same methodology to determine which method is best for a particular dataset that I am working with. However, I run into trouble when trying the ROSE algorithm: it creates negative numeric values when they should be positive. Is there a solution to this? Should all the variables be converted into factors? If anyone has encountered the problem, how did you overcome it?
Very good article! Thank you.