Deep learning models are based on activation functions that provide non-linearity and enable networks to learn complicated patterns. This article will discuss the Softplus activation function, what it is, and how it can be used in PyTorch. Softplus can be said to be a smooth form of the popular ReLU activation, that mitigates the drawbacks of ReLU but introduces its own drawbacks. We will discuss what Softplus is, its mathematical formula, its comparison with ReLU, what its advantages and limitations are and take a stroll through some PyTorch code utilizing it.
Table of contents
What is Softplus Activation Function?
Softplus activation function is a non-linear function of neural networks and is characterized by a smooth approximation of the ReLU function. In easier words, Softplus acts like ReLU in cases when the positive or negative input is very large, but a sharp corner at the zero point is absent. In its place, it rises smoothly and yields a marginal positive output to negative inputs instead of a firm zero. This continuous and differentiable behavior implies that Softplus is continuous and differentiable everywhere in contrast to ReLU which is discontinuous (with a sharp change of slope) at x = 0.
Why is Softplus used?
Softplus is selected by developers that prefer a more convenient activation that offers. non-zero gradients also where ReLU would otherwise be inactive. Gradient-based optimization can be spared major disruptions caused by the smoothness of Softplus (the gradient is shifting smoothly instead of stepping). It also inherently clips outputs (as ReLU does) yet the clipping is not to zero. In summary, Softplus is the softer version of ReLU: it is ReLU-like when the value is large but is better around zero and is nice and smooth.
Softplus Mathematical Formula
The Softplus is mathematically defined to be:
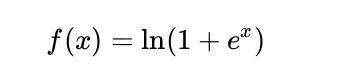
When x is large, ex is very large and therefore, ln(1 + ex) is very similar to ln(ex), equal to x. It implies that Softplus is nearly linear at large inputs, such as ReLU.
When x is large and negative, ex is very small, thus ln(1 + ex) is nearly ln(1), and this is 0. The values produced by Softplus are close to zero but never zero. To take on a value that is zero, x must approach negative infinity.
Another thing that is handy is that the derivative of Softplus is the sigmoid. The derivative of ln(1 + ex) is:
ex / (1 + ex)
This is the very sigmoid of x. It implies that at any moment, the slope of Softplus is sigmoid(x), that is, it has a non-zero gradient everywhere and is smooth. This renders Softplus useful in gradient-based learning since it does not have flat areas where the gradients vanish.
Using Softplus in PyTorch
PyTorch provides the activation Softplus as a native activation and thus can be easily used like ReLU or any other activation. An example of two simple ones is given below. The former uses Softplus on a small number of test values, and the latter demonstrates how to insert Softplus into a small neural network.
Softplus on Sample Inputs
The snippet below applies nn.Softplus to a small tensor so you can see how it behaves with negative, zero, and positive inputs.
import torch
import torch.nn as nn
# Create the Softplus activation
softplus = nn.Softplus() # default beta=1, threshold=20
# Sample inputs
x = torch.tensor([-2.0, -1.0, 0.0, 1.0, 2.0])
y = softplus(x)
print("Input:", x.tolist())
print("Softplus output:", y.tolist())
What this shows:
- At x = -2 and x = -1, the value of Softplus is small positive values rather than 0.
- The output is approximately 0.6931 at x =0, i.e. ln(2)
- In case of positive inputs such as 1 or 2, the results are a little bigger than the inputs since Softplus smoothes the curve. Softplus is approaching x as it increases.
The Softplus of PyTorch is represented by the formula ln(1 + exp(betax)). Its internal threshold value of 20 is to prevent a numerical overflow. Softplus is linear in large betax, meaning that in that case of PyTorch simply returns x.
Using Softplus in a Neural Network
Here is a simple PyTorch network that uses Softplus as the activation for its hidden layer.
import torch
import torch.nn as nn
class SimpleNet(nn.Module):
def __init__(self, input_size, hidden_size, output_size):
super(SimpleNet, self).__init__()
self.fc1 = nn.Linear(input_size, hidden_size)
self.activation = nn.Softplus()
self.fc2 = nn.Linear(hidden_size, output_size)
def forward(self, x):
x = self.fc1(x)
x = self.activation(x) # apply Softplus
x = self.fc2(x)
return x
# Create the model
model = SimpleNet(input_size=4, hidden_size=3, output_size=1)
print(model)
Passing an input through the model works as usual:
x_input = torch.randn(2, 4) # batch of 2 samples
y_output = model(x_input)
print("Input:\n", x_input)
print("Output:\n", y_output)
In this arrangement, Softplus activation is used so that the values exited in the first layer to the second layer are non-negative. The replacement of Softplus by an existing model may not need any other structural variation. It is only important to remember that Softplus might be a little slower in training and require more computation than ReLU.
The final layer may also be implemented with Softplus when there are positive values that a model should generate as outputs, e.g. scale parameters or positive regression objectives.
Softplus vs ReLU: Comparison Table
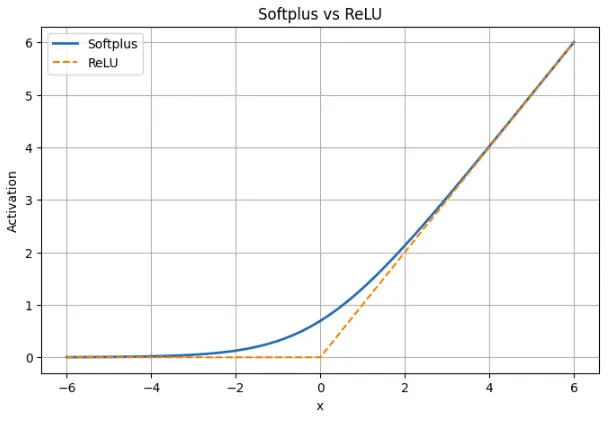
| Aspect | Softplus | ReLU |
|---|---|---|
| Definition | f(x) = ln(1 + ex) | f(x) = max(0, x) |
| Shape | Smooth transition across all x | Sharp kink at x = 0 |
| Behavior for x < 0 | Small positive output; never reaches zero | Output is exactly zero |
| Example at x = -2 | Softplus ≈ 0.13 | ReLU = 0 |
| Near x = 0 | Smooth and differentiable; value ≈ 0.693 | Not differentiable at 0 |
| Behavior for x > 0 | Almost linear, closely matches ReLU | Linear with slope 1 |
| Example at x = 5 | Softplus ≈ 5.0067 | ReLU = 5 |
| Gradient | Always non-zero; derivative is sigmoid(x) | Zero for x < 0, undefined at 0 |
| Risk of dead neurons | None | Possible for negative inputs |
| Sparsity | Does not produce exact zeros | Produces true zeros |
| Training effect | Stable gradient flow, smoother updates | Simple but can stop learning for some neurons |
An analog of ReLU is softplus. It is ReLU with very large positive or negative inputs but with the corner at zero removed. This prevents dead neurons as the gradient does not go to a zero. This comes at the price that Softplus does not generate true zeros meaning that it is not as sparse as ReLU. Softplus provides more comfortable training dynamics in the practice, but ReLU is still used because it is faster and simpler.
Benefits of Using Softplus
Softplus has some practical benefits that render it to be useful in some models.
- Everywhere smooth and differentiable
There are no sharp corners in Softplus. It is entirely differentiable to every input. This assists in maintaining gradients that may end up making optimization a little easier since the loss varies slower.
- Avoids dead neurons
ReLU can prevent updating when a neuron continuously gets negative input, as the gradient will be zero. Softplus does not give the exact zero value on negative numbers and thus all the neurons remain partially active and are updated on the gradient.
- Reacts more favorably to negative inputs
Softplus does not throw out the negative inputs by generating a zero value as ReLU does but rather generates a small positive value. This allows the model to retain a part of information of negative signals rather than losing all of it.
Concisely, Softplus maintains gradients flowing, prevents dead neurons and offers smooth behavior to be used in some architectures or tasks where continuity is important.
Limitations and Trade-offs of Softplus
There are also disadvantages of Softplus that restrict the frequency of its usage.
- More expensive to compute
Softplus uses exponential and logarithmic operations that are slower than the simple max(0, x) of ReLU. This additional overhead can be visibly felt on large models because ReLU is extremely optimized on most hardware.
- No true sparsity
ReLU generates perfect zeroes on negative examples, which can save computing time and occasionally aid in regularization. Softplus does not give a real zero and hence all the neurons are always not inactive. This eliminates the risk of dead neurons as well as the efficiency advantages of sparse activations.
- Gradually slow down the convergence of deep networks
ReLU is commonly used to train deep models. It has a sharp cutoff and linear positive region which can force learning. Softplus is smoother and might have slow updates particularly in very deep networks where the difference between layers is small.
To summarize, Softplus has nice mathematical properties and avoids issues like dead neurons, but these benefits don’t always translate to better results in deep networks. It is best used in cases where smoothness or positive outputs are important, rather than as a universal replacement for ReLU.
Conclusion
Softplus provides smooth, soft alternatives of ReLU to the neural networks. It learns gradients, does not kill neurons and is fully differentiable throughout the inputs. It is like ReLU at large values, but at zero, behaves more like a constant than ReLU because it produces non-zero output and slope. Meanwhile, it is associated with trade-offs. It is also slower to compute; it also does not generate real zeros and may not accelerate learning in deep networks as quickly as ReLU. Softplus is more effective in models, where gradients are smooth or where positive outputs are mandatory. In most other scenarios, it is a useful alternative to a default replacement of ReLU.
Frequently Asked Questions
A. Softplus prevents dead neurons by keeping gradients non-zero for all inputs, offering a smooth alternative to ReLU while still behaving similarly for large positive values.
A. It’s a good choice when your model benefits from smooth gradients or must output strictly positive values, like scale parameters or certain regression targets.
A. It’s slower to compute than ReLU, doesn’t create sparse activations, and can lead to slightly slower convergence in deep networks.





