24 minutes
Introduction
Time Series (referred as TS from now) is considered to be one of the less known skills in the data science space (Even I had little clue about it a couple of days back). I set myself on a journey to learn the basic steps for solving a Time Series problem and here I am sharing the same with you. These will definitely help you get a decent model in any future project you take up!
Before going through this article, I highly recommend reading A Complete Tutorial on Time Series Modeling in R and taking the free Time Series Forecasting course. It focuses on fundamental concepts and I will focus on using these concepts in solving a problem end-to-end along with codes in Python. Many resources exist for time series in R but very few are there for Python so I’ll be using Python in this article.
Are you a beginner looking for a place to start your data science journey? Here is a comprehensive course to assist you in your journey. Master Time Series, Machine Learning and Deep Learning through our Certified Blackbelt Program-
Learning Objectives:
- Learn the steps to create a Time Series forecast.
- Additional focus on Dickey-Fuller test & ARIMA (Autoregressive, moving average) models.
- Learn the concepts theoretically as well as with their implementation in python.
Table of Contents
What Is Time Series?
As the name suggests, TS is a collection of data points collected at constant time intervals. These are analyzed to determine the long term trend so as to forecast the future or perform some other form of analysis. But what makes a TS different from say a regular regression problem? There are 2 things:
- It is time dependent. So the basic assumption of a linear regression model that the observations are independent doesn’t hold in this case.
- Along with an increasing or decreasing trend, most TS have some form of seasonality trends, i.e. variations specific to a particular time frame. For example, if you see the sales of a woolen jacket over time, you will invariably find higher sales in winter seasons.
Because of the inherent properties of a TS, there are various steps involved in analyzing it. These are discussed in detail below. Lets start by loading a TS object in Python. We’ll be using the popular AirPassengers data set which can be downloaded here.
Please note that the aim of this article is to familiarize you with the various techniques used for TS in general. The example considered here is just for illustration and I will focus on coverage a breadth of topics and not making a very accurate forecast.
Loading and Handling Time Series in Pandas
Pandas has dedicated libraries for handling TS objects, particularly the datatime64[ns] class which stores time information and allows us to perform some operations really fast. Lets start by firing up the required libraries:
Month,#Passengers
1949-01,112
1949-02,118
1949-03,132
1949-04,129
1949-05,121
1949-06,135
1949-07,148
1949-08,148
1949-09,136
1949-10,119
1949-11,104
1949-12,118
1950-01,115
1950-02,126
1950-03,141
1950-04,135
1950-05,125
1950-06,149
1950-07,170
1950-08,170
1950-09,158
1950-10,133
1950-11,114
1950-12,140
1951-01,145
1951-02,150
1951-03,178
1951-04,163
1951-05,172
1951-06,178
1951-07,199
1951-08,199
1951-09,184
1951-10,162
1951-11,146
1951-12,166
1952-01,171
1952-02,180
1952-03,193
1952-04,181
1952-05,183
1952-06,218
1952-07,230
1952-08,242
1952-09,209
1952-10,191
1952-11,172
1952-12,194
1953-01,196
1953-02,196
1953-03,236
1953-04,235
1953-05,229
1953-06,243
1953-07,264
1953-08,272
1953-09,237
1953-10,211
1953-11,180
1953-12,201
1954-01,204
1954-02,188
1954-03,235
1954-04,227
1954-05,234
1954-06,264
1954-07,302
1954-08,293
1954-09,259
1954-10,229
1954-11,203
1954-12,229
1955-01,242
1955-02,233
1955-03,267
1955-04,269
1955-05,270
1955-06,315
1955-07,364
1955-08,347
1955-09,312
1955-10,274
1955-11,237
1955-12,278
1956-01,284
1956-02,277
1956-03,317
1956-04,313
1956-05,318
1956-06,374
1956-07,413
1956-08,405
1956-09,355
1956-10,306
1956-11,271
1956-12,306
1957-01,315
1957-02,301
1957-03,356
1957-04,348
1957-05,355
1957-06,422
1957-07,465
1957-08,467
1957-09,404
1957-10,347
1957-11,305
1957-12,336
1958-01,340
1958-02,318
1958-03,362
1958-04,348
1958-05,363
1958-06,435
1958-07,491
1958-08,505
1958-09,404
1958-10,359
1958-11,310
1958-12,337
1959-01,360
1959-02,342
1959-03,406
1959-04,396
1959-05,420
1959-06,472
1959-07,548
1959-08,559
1959-09,463
1959-10,407
1959-11,362
1959-12,405
1960-01,417
1960-02,391
1960-03,419
1960-04,461
1960-05,472
1960-06,535
1960-07,622
1960-08,606
1960-09,508
1960-10,461
1960-11,390
1960-12,432
Let’s understand the arguments one by one:
- parse_dates: This specifies the column which contains the date-time information. As we say above, the column name is ‘Month’.
- index_col: A key idea behind using Pandas for TS data is that the index has to be the variable depicting date-time information. So this argument tells pandas to use the ‘Month’ column as index.
- date_parser: This specifies a function which converts an input string into datetime variable. Be default Pandas reads data in format ‘YYYY-MM-DD HH:MM:SS’. If the data is not in this format, the format has to be manually defined. Something similar to the dataparse function defined here can be used for this purpose.
Now we can see that the data has time object as index and #Passengers as the column. We can cross-check the datatype of the index with the following command:
data.index
Notice the dtype=’datetime[ns]’ which confirms that it is a datetime object. As a personal preference, I would convert the column into a Series object to prevent referring to columns names every time I use the TS. Please feel free to use as a dataframe is that works better for you.
ts = data[‘#Passengers’]
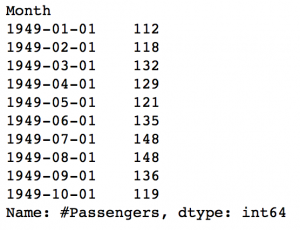
ts.head(10)
Before going further, I’ll discuss some indexing techniques for TS data. Lets start by selecting a particular value in the Series object. This can be done in following 2 ways:
#1. Specific the index as a string constant: ts['1949-01-01'] #2. Import the datetime library and use 'datetime' function: from datetime import datetime ts[datetime(1949,1,1)]
Both would return the value ‘112’ which can also be confirmed from previous output. Suppose we want all the data upto May 1949. This can be done in 2 ways:
#1. Specify the entire range: ts['1949-01-01':'1949-05-01'] #2. Use ':' if one of the indices is at ends: ts[:'1949-05-01']
Both would yield following output:
There are 2 things to note here:
- Unlike numeric indexing, the end index is included here. For instance, if we index a list as a[:5] then it would return the values at indices – [0,1,2,3,4]. But here the index ‘1949-05-01’ was included in the output.
- The indices have to be sorted for ranges to work. If you randomly shuffle the index, this won’t work.
Consider another instance where you need all the values of the year 1949. This can be done as:
ts['1949']
The month part was omitted. Similarly if you all days of a particular month, the day part can be omitted.
Now, lets move onto the analyzing the TS.
How to Check the Stationarity of a Time Series?
A TS is said to be stationary if its statistical properties such as mean, variance remain constant over time. But why is it important? Most of the TS models work on the assumption that the TS is stationary. Intuitively, we can sat that if a TS has a particular behaviour over time, there is a very high probability that it will follow the same in the future. Also, the theories related to stationary series are more mature and easier to implement as compared to non-stationary series.
Stationarity is defined using very strict criterion. However, for practical purposes we can assume the series to be stationary if it has constant statistical properties over time, ie. the following:
- constant mean
- constant variance
- an autocovariance that does not depend on time.
I’ll skip the details as it is very clearly defined in this article. Lets move onto the ways of testing stationarity. First and foremost is to simple plot the data and analyze visually. The data can be plotted using following command:
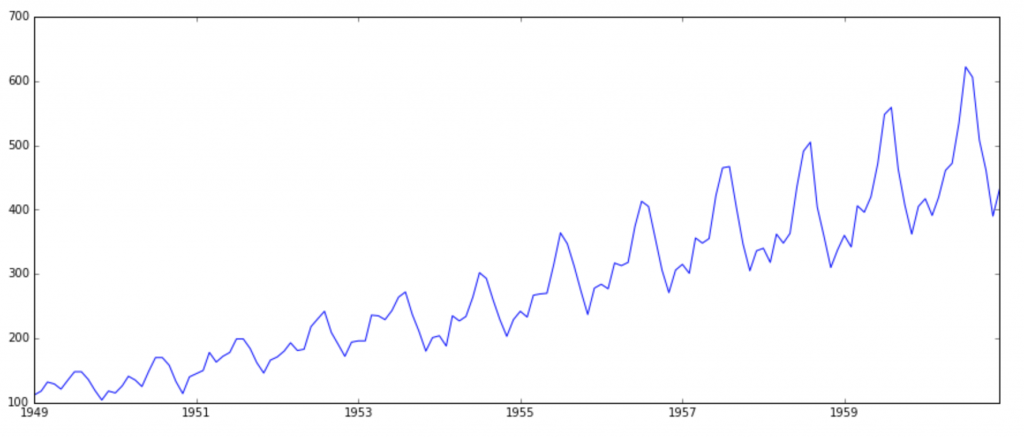
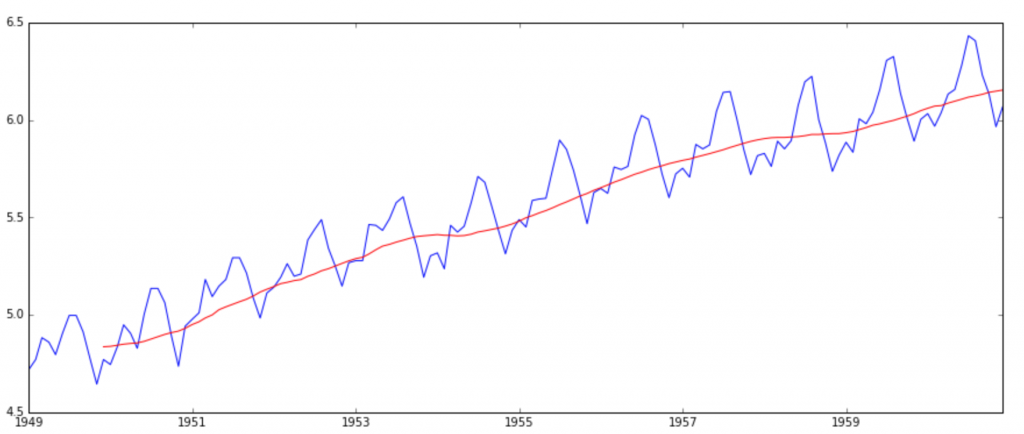
plt.plot(ts)
It is clearly evident that there is an overall increasing trend in the data along with some seasonal variations. However, it might not always be possible to make such visual inferences (we’ll see such cases later). So, more formally, we can check stationarity using the following:
- Plotting Rolling Statistics: We can plot the moving average or moving variance and see if it varies with time. By moving average/variance I mean that at any instant ‘t’, we’ll take the average/variance of the last year, i.e. last 12 months. But again this is more of a visual technique.
- Dickey-Fuller Test: This is one of the statistical tests for checking stationarity. Here the null hypothesis is that the TS is non-stationary. The test results comprise of a Test Statistic and some Critical Values for difference confidence levels. If the ‘Test Statistic’ is less than the ‘Critical Value’, we can reject the null hypothesis and say that the series is stationary. Refer this article for details.
These concepts might not sound very intuitive at this point. I recommend going through the prequel article. If you’re interested in some theoretical statistics, you can refer Introduction to Time Series and Forecasting by Brockwell and Davis. The book is a bit stats-heavy, but if you have the skill to read-between-lines, you can understand the concepts and tangentially touch the statistics.
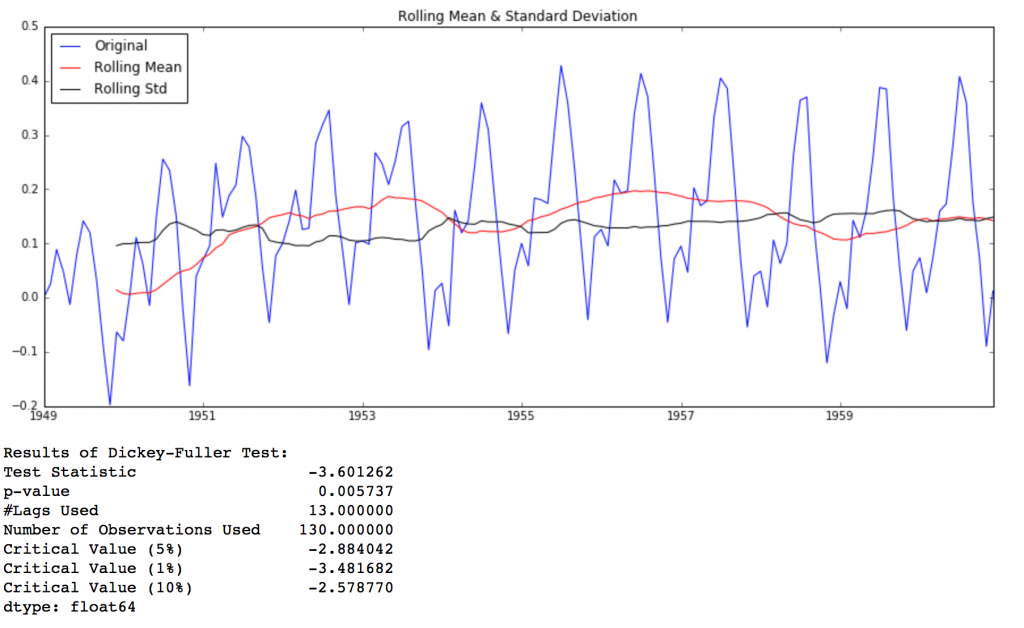
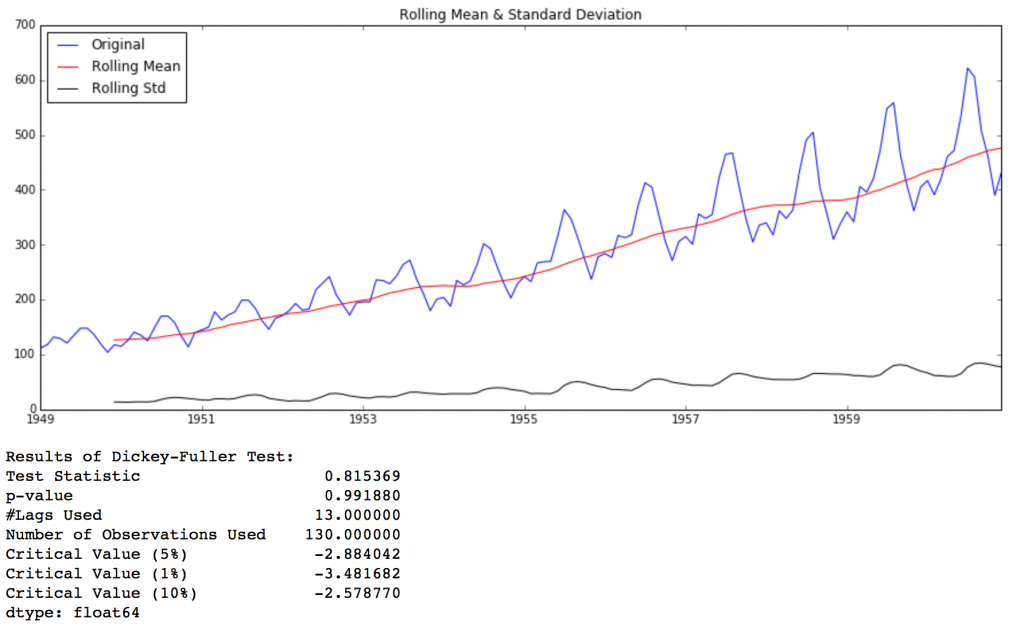
Back to checking stationarity, we’ll be using the rolling statistics plots along with Dickey-Fuller test results a lot so I have defined a function which takes a TS as input and generated them for us. Please note that I’ve plotted standard deviation instead of variance to keep the unit similar to mean.
from statsmodels.tsa.stattools import adfuller
def test_stationarity(timeseries):
#Determing rolling statistics
rolmean = pd.rolling_mean(timeseries, window=12)
rolstd = pd.rolling_std(timeseries, window=12)
#Plot rolling statistics:
orig = plt.plot(timeseries, color='blue',label='Original')
mean = plt.plot(rolmean, color='red', label='Rolling Mean')
std = plt.plot(rolstd, color='black', label = 'Rolling Std')
plt.legend(loc='best')
plt.title('Rolling Mean & Standard Deviation')
plt.show(block=False)
#Perform Dickey-Fuller test:
print 'Results of Dickey-Fuller Test:'
dftest = adfuller(timeseries, autolag='AIC')
dfoutput = pd.Series(dftest[0:4], index=['Test Statistic','p-value','#Lags Used','Number of Observations Used'])
for key,value in dftest[4].items():
dfoutput['Critical Value (%s)'%key] = value
print dfoutput
The code is pretty straight forward. Please feel free to discuss the code in comments if you face challenges in grasping it.
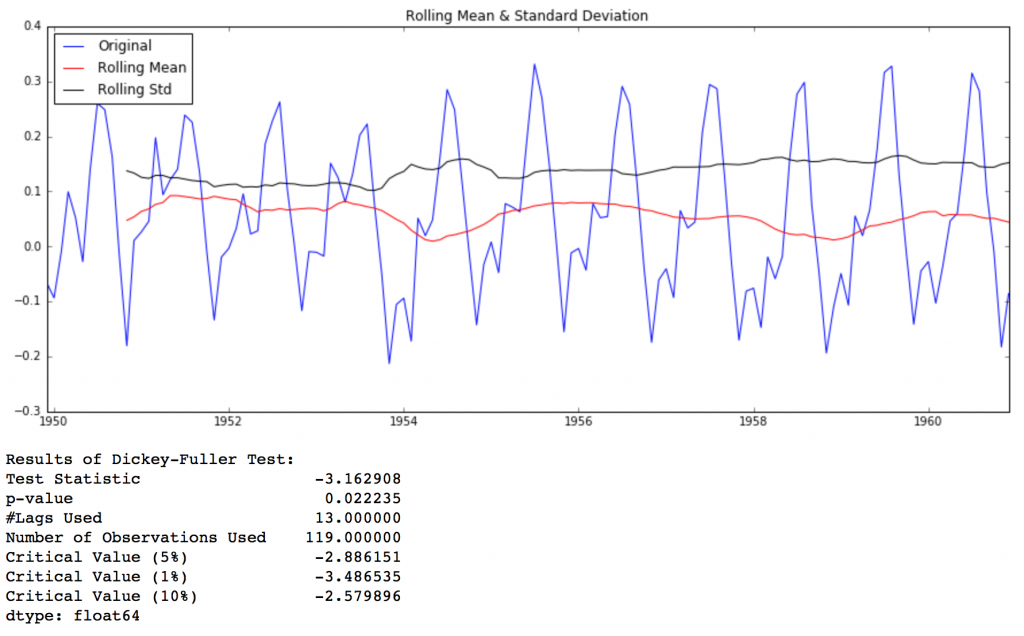
Let’s run it for our input series:
test_stationarity(ts)
Though the variation in standard deviation is small, mean is clearly increasing with time and this is not a stationary series. Also, the test statistic is way more than the critical values. Note that the signed values should be compared and not the absolute values.
Next, we’ll discuss the techniques that can be used to take this TS towards stationarity.
How to Make a Time Series Stationary?
Though stationarity assumption is taken in many TS models, almost none of practical time series are stationary. So statisticians have figured out ways to make series stationary, which we’ll discuss now. Actually, its almost impossible to make a series perfectly stationary, but we try to take it as close as possible.
Lets understand what is making a TS non-stationary. There are 2 major reasons behind non-stationaruty of a TS:
1. Trend – varying mean over time. For eg, in this case we saw that on average, the number of passengers was growing over time.
2. Seasonality – variations at specific time-frames. eg people might have a tendency to buy cars in a particular month because of pay increment or festivals.
The underlying principle is to model or estimate the trend and seasonality in the series and remove those from the series to get a stationary series. Then statistical forecasting techniques can be implemented on this series. The final step would be to convert the forecasted values into the original scale by applying trend and seasonality constraints back.
Note: I’ll be discussing a number of methods. Some might work well in this case and others might not. But the idea is to get a hang of all the methods and not focus on just the problem at hand.
Let’s start by working on the trend part.
Estimating & Eliminating Trend
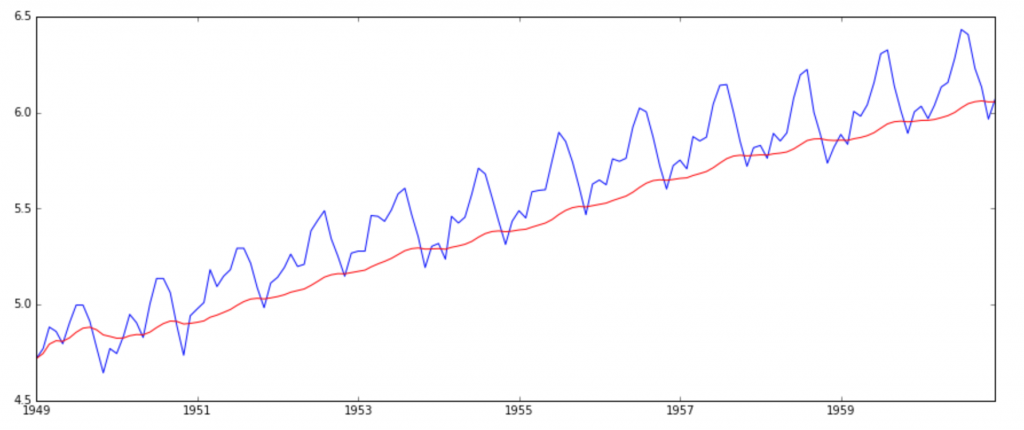
One of the first tricks to reduce trend can be transformation. For example, in this case we can clearly see that the there is a significant positive trend. So we can apply transformation which penalize higher values more than smaller values. These can be taking a log, square root, cube root, etc. Lets take a log transform here for simplicity:
ts_log = np.log(ts) plt.plot(ts_log)
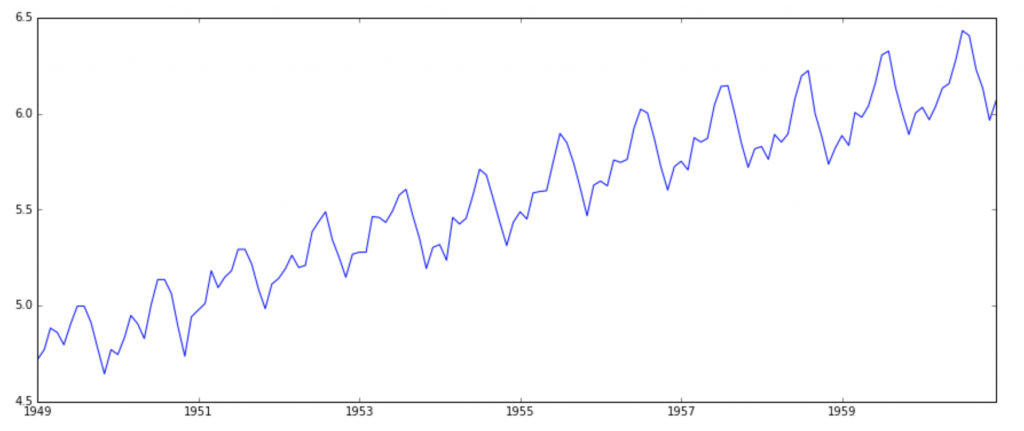
In this simpler case, it is easy to see a forward trend in the data. But its not very intuitive in presence of noise. So we can use some techniques to estimate or model this trend and then remove it from the series. There can be many ways of doing it and some of most commonly used are:
- Aggregation – taking average for a time period like monthly/weekly averages
- Smoothing – taking rolling averages
- Polynomial Fitting – fit a regression model
I will discuss smoothing here and you should try other techniques as well which might work out for other problems. Smoothing refers to taking rolling estimates, i.e. considering the past few instances. There are can be various ways but I will discuss two of those here.
Moving Average
In this approach, we take average of ‘k’ consecutive values depending on the frequency of time series. Here we can take the average over the past 1 year, i.e. last 12 values. Pandas has specific functions defined for determining rolling statistics.
moving_avg = pd.rolling_mean(ts_log,12) plt.plot(ts_log) plt.plot(moving_avg, color='red')
The red line shows the rolling mean. Lets subtract this from the original series. Note that since we are taking average of last 12 values, rolling mean is not defined for first 11 values. This can be observed as:
ts_log_moving_avg_diff = ts_log - moving_avg ts_log_moving_avg_diff.head(12)
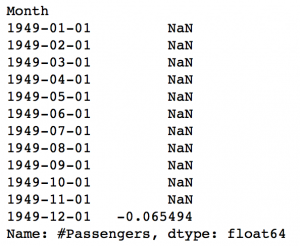
Notice the first 11 being Nan. Lets drop these NaN values and check the plots to test stationarity.
ts_log_moving_avg_diff.dropna(inplace=True) test_stationarity(ts_log_moving_avg_diff)
This looks like a much better series. The rolling values appear to be varying slightly but there is no specific trend. Also, the test statistic is smaller than the 5% critical values so we can say with 95% confidence that this is a stationary series.
However, a drawback in this particular approach is that the time-period has to be strictly defined. In this case we can take yearly averages but in complex situations like forecasting a stock price, its difficult to come up with a number. So we take a ‘weighted moving average’ where more recent values are given a higher weight. There can be many technique for assigning weights. A popular one is exponentially weighted moving average where weights are assigned to all the previous values with a decay factor. Find details here. This can be implemented in Pandas as:
expwighted_avg = pd.ewma(ts_log, halflife=12) plt.plot(ts_log) plt.plot(expwighted_avg, color='red')
Note that here the parameter ‘halflife’ is used to define the amount of exponential decay. This is just an assumption here and would depend largely on the business domain. Other parameters like span and center of mass can also be used to define decay which are discussed in the link shared above. Now, let’s remove this from series and check stationarity:
ts_log_ewma_diff = ts_log - expwighted_avg test_stationarity(ts_log_ewma_diff)
This TS has even lesser variations in mean and standard deviation in magnitude. Also, the test statistic is smaller than the 1% critical value, which is better than the previous case. Note that in this case, there will be no missing values as all values from starting are given weights. So it’ll work even with no previous values.
Eliminating Trend and Seasonality
The simple trend reduction techniques discussed before don’t work in all cases, particularly the ones with high seasonality. Let’s discuss two ways of removing trend and seasonality:
- Differencing – taking the difference with a particular time lag
- Decomposition – modeling both trend and seasonality and removing them from the model
Differencing
One of the most common methods of dealing with both trend and seasonality is differencing. In this technique, we take the difference of the observation at a particular instant with that at the previous instant. This mostly works well in improving stationarity. First-order differencing can be done in Pandas as:
ts_log_diff = ts_log - ts_log.shift() plt.plot(ts_log_diff)
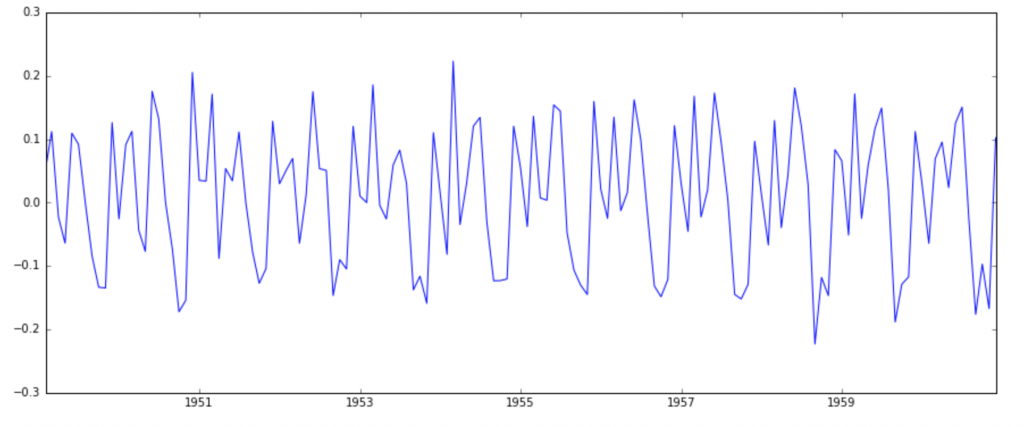
This appears to have reduced trend considerably. Lets verify using our plots:
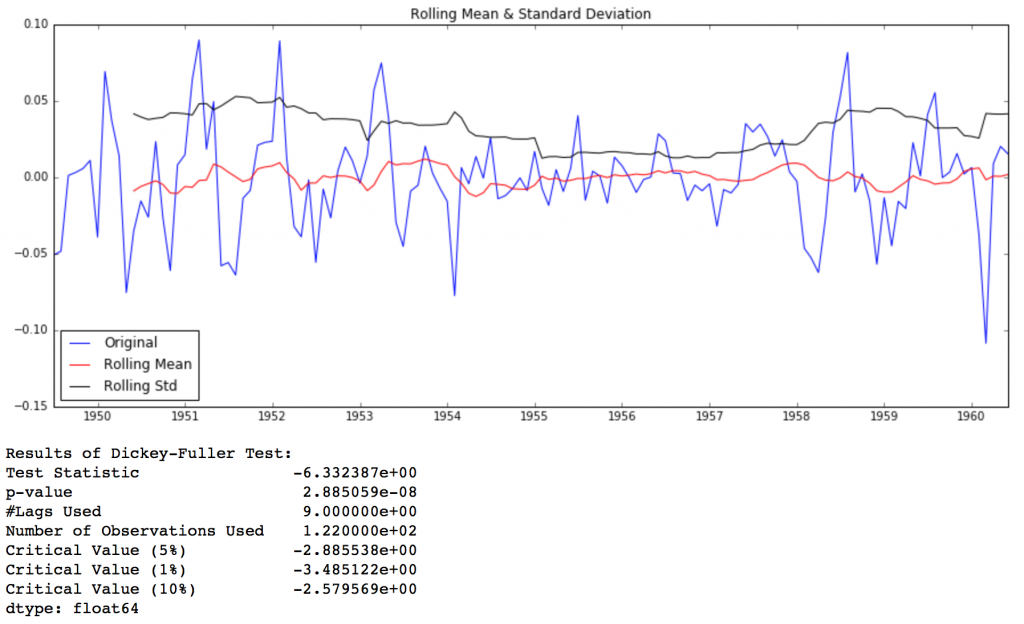
ts_log_diff.dropna(inplace=True) test_stationarity(ts_log_diff)
We can see that the mean and std variations have small variations with time. Also, the Dickey-Fuller test statistic is less than the 10% critical value, thus the TS is stationary with 90% confidence. We can also take second or third order differences which might get even better results in certain applications. I leave it to you to try them out.
Decomposing
In this approach, both trend and seasonality are modeled separately and the remaining part of the series is returned. I’ll skip the statistics and come to the results:
from statsmodels.tsa.seasonal import seasonal_decompose decomposition = seasonal_decompose(ts_log) trend = decomposition.trend seasonal = decomposition.seasonal residual = decomposition.resid plt.subplot(411) plt.plot(ts_log, label='Original') plt.legend(loc='best') plt.subplot(412) plt.plot(trend, label='Trend') plt.legend(loc='best') plt.subplot(413) plt.plot(seasonal,label='Seasonality') plt.legend(loc='best') plt.subplot(414) plt.plot(residual, label='Residuals') plt.legend(loc='best') plt.tight_layout()
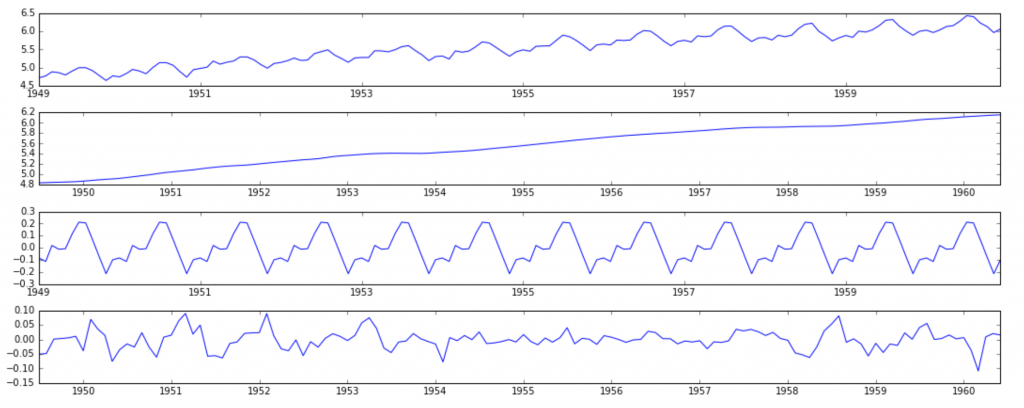
Here we can see that the trend, seasonality are separated out from data and we can model the residuals. Lets check stationarity of residuals:
ts_log_decompose = residual ts_log_decompose.dropna(inplace=True) test_stationarity(ts_log_decompose)
The Dickey-Fuller test statistic is significantly lower than the 1% critical value. So this TS is very close to stationary. You can try advanced decomposition techniques as well which can generate better results. Also, you should note that converting the residuals into original values for future data in not very intuitive in this case.
Forecasting a Time Series
We saw different techniques and all of them worked reasonably well for making the TS stationary. Lets make model on the TS after differencing as it is a very popular technique. Also, its relatively easier to add noise and seasonality back into predicted residuals in this case. Having performed the trend and seasonality estimation techniques, there can be two situations:
- A strictly stationary series with no dependence among the values. This is the easy case wherein we can model the residuals as white noise. But this is very rare.
- A series with significant dependence among values. In this case we need to use some statistical models like ARIMA to forecast the data.
Let me give you a brief introduction to ARIMA. I won’t go into the technical details but you should understand these concepts in detail if you wish to apply them more effectively. ARIMA stands for Auto-Regressive Integrated Moving Averages. The ARIMA forecasting for a stationary time series is nothing but a linear (like a linear regression) equation. The predictors depend on the parameters (p,d,q) of the ARIMA model:
- Number of AR (Auto-Regressive) terms (p): AR terms are just lags of dependent variable. For instance if p is 5, the predictors for x(t) will be x(t-1)….x(t-5).
- Number of MA (Moving Average) terms (q): MA terms are lagged forecast errors in prediction equation. For instance if q is 5, the predictors for x(t) will be e(t-1)….e(t-5) where e(i) is the difference between the moving average at ith instant and actual value.
- Number of Differences (d): These are the number of nonseasonal differences, i.e. in this case we took the first order difference. So either we can pass that variable and put d=0 or pass the original variable and put d=1. Both will generate same results.
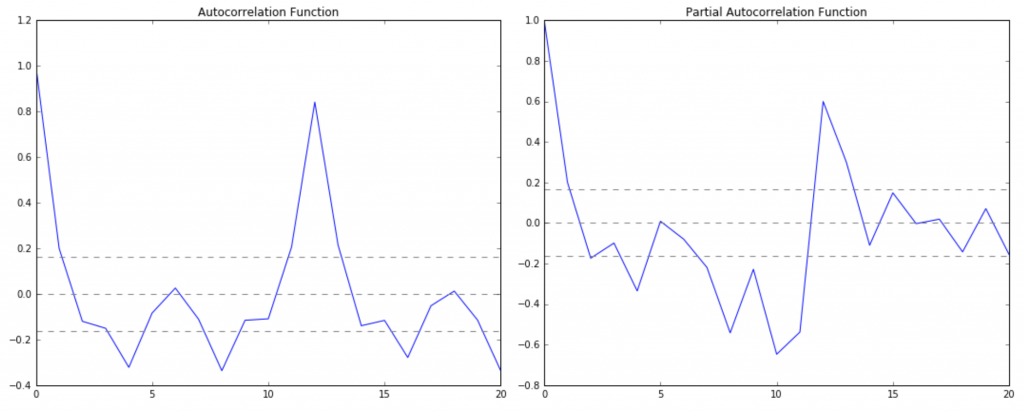
An importance concern here is how to determine the value of ‘p’ and ‘q’. We use two plots to determine these numbers. Lets discuss them first.
- Autocorrelation Function (ACF): It is a measure of the correlation between the the TS with a lagged version of itself. For instance at lag 5, ACF would compare series at time instant ‘t1’…’t2’ with series at instant ‘t1-5’…’t2-5’ (t1-5 and t2 being end points).
- Partial Autocorrelation Function (PACF): This measures the correlation between the TS with a lagged version of itself but after eliminating the variations already explained by the intervening comparisons. Eg at lag 5, it will check the correlation but remove the effects already explained by lags 1 to 4.
The ACF and PACF plots for the TS after differencing can be plotted as:
#ACF and PACF plots: from statsmodels.tsa.stattools import acf, pacf
lag_acf = acf(ts_log_diff, nlags=20) lag_pacf = pacf(ts_log_diff, nlags=20, method='ols')
#Plot ACF:
plt.subplot(121)
plt.plot(lag_acf)
plt.axhline(y=0,linestyle='--',color='gray')
plt.axhline(y=-1.96/np.sqrt(len(ts_log_diff)),linestyle='--',color='gray')
plt.axhline(y=1.96/np.sqrt(len(ts_log_diff)),linestyle='--',color='gray')
plt.title('Autocorrelation Function')
#Plot PACF:
plt.subplot(122)
plt.plot(lag_pacf)
plt.axhline(y=0,linestyle='--',color='gray')
plt.axhline(y=-1.96/np.sqrt(len(ts_log_diff)),linestyle='--',color='gray')
plt.axhline(y=1.96/np.sqrt(len(ts_log_diff)),linestyle='--',color='gray')
plt.title('Partial Autocorrelation Function')
plt.tight_layout()
In this plot, the two dotted lines on either sides of 0 are the confidence interevals. These can be used to determine the ‘p’ and ‘q’ values as:
- p – The lag value where the PACF chart crosses the upper confidence interval for the first time. If you notice closely, in this case p=2.
- q – The lag value where the ACF chart crosses the upper confidence interval for the first time. If you notice closely, in this case q=2.
Now, lets make 3 different ARIMA models considering individual as well as combined effects. I will also print the RSS for each. Please note that here RSS is for the values of residuals and not actual series.
We need to load the ARIMA model first:
from statsmodels.tsa.arima_model import ARIMA
The p,d,q values can be specified using the order argument of ARIMA which take a tuple (p,d,q). Let model the 3 cases:
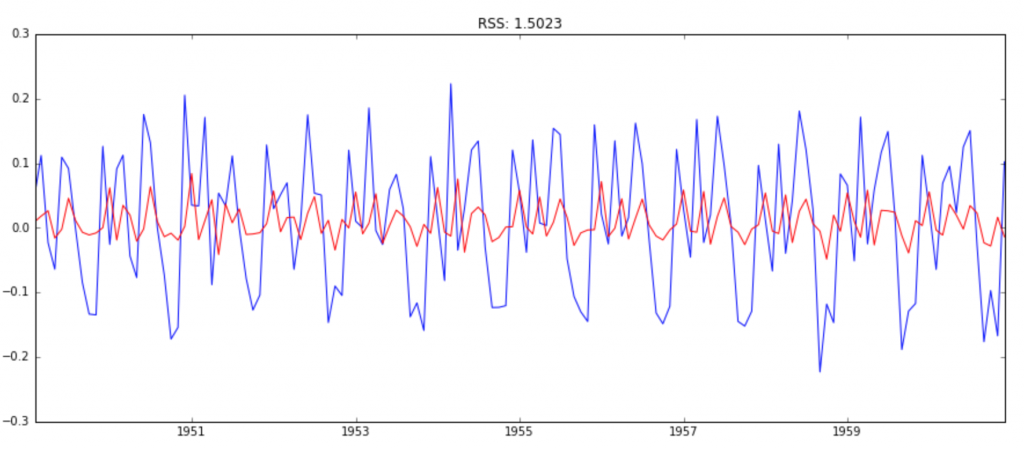
AR Model
model = ARIMA(ts_log, order=(2, 1, 0))
results_AR = model.fit(disp=-1)
plt.plot(ts_log_diff)
plt.plot(results_AR.fittedvalues, color='red')
plt.title('RSS: %.4f'% sum((results_AR.fittedvalues-ts_log_diff)**2))
MA Model
model = ARIMA(ts_log, order=(0, 1, 2))
results_MA = model.fit(disp=-1)
plt.plot(ts_log_diff)
plt.plot(results_MA.fittedvalues, color='red')
plt.title('RSS: %.4f'% sum((results_MA.fittedvalues-ts_log_diff)**2))
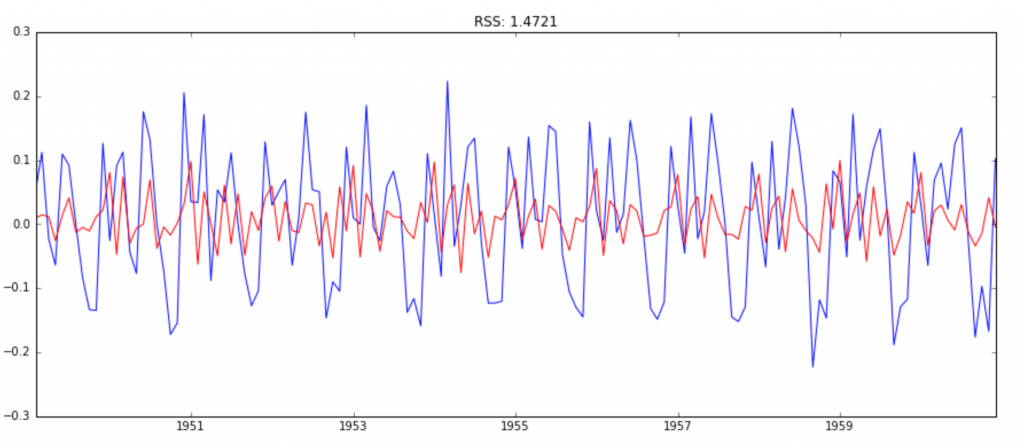
Combined Model
model = ARIMA(ts_log, order=(2, 1, 2))
results_ARIMA = model.fit(disp=-1)
plt.plot(ts_log_diff)
plt.plot(results_ARIMA.fittedvalues, color='red')
plt.title('RSS: %.4f'% sum((results_ARIMA.fittedvalues-ts_log_diff)**2))
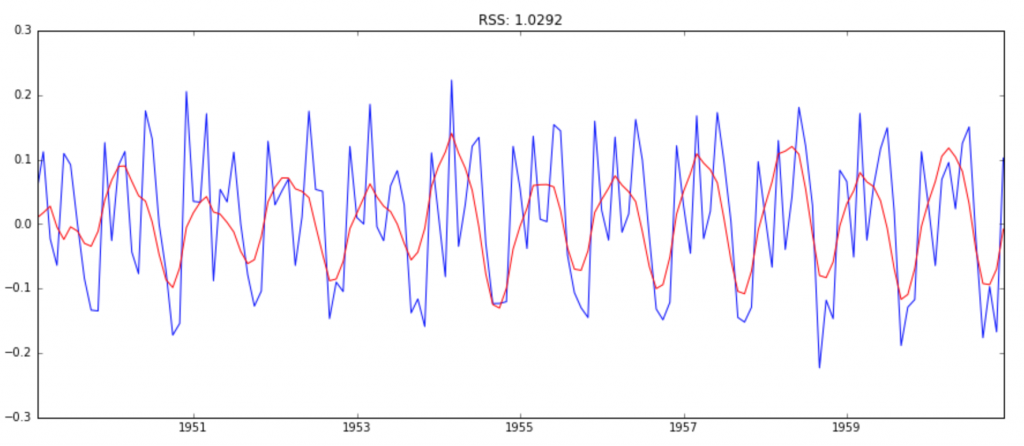
Here we can see that the AR and MA models have almost the same RSS but combined is significantly better. Now, we are left with 1 last step, i.e. taking these values back to the original scale.
Taking it back to original scale
Since the combined model gave best result, lets scale it back to the original values and see how well it performs there. First step would be to store the predicted results as a separate series and observe it.
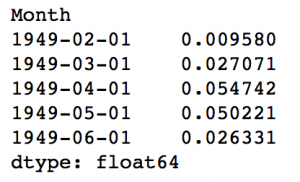
predictions_ARIMA_diff = pd.Series(results_ARIMA.fittedvalues, copy=True) print predictions_ARIMA_diff.head()
Notice that these start from ‘1949-02-01’ and not the first month. Why? This is because we took a lag by 1 and first element doesn’t have anything before it to subtract from. The way to convert the differencing to log scale is to add these differences consecutively to the base number. An easy way to do it is to first determine the cumulative sum at index and then add it to the base number. The cumulative sum can be found as:
predictions_ARIMA_diff_cumsum = predictions_ARIMA_diff.cumsum() print predictions_ARIMA_diff_cumsum.head()
You can quickly do some back of mind calculations using previous output to check if these are correct. Next we’ve to add them to base number. For this lets create a series with all values as base number and add the differences to it. This can be done as:
predictions_ARIMA_log = pd.Series(ts_log.ix[0], index=ts_log.index) predictions_ARIMA_log = predictions_ARIMA_log.add(predictions_ARIMA_diff_cumsum,fill_value=0) predictions_ARIMA_log.head()
Here the first element is base number itself and from thereon the values cumulatively added. Last step is to take the exponent and compare with the original series.
predictions_ARIMA = np.exp(predictions_ARIMA_log)
plt.plot(ts)
plt.plot(predictions_ARIMA)
plt.title('RMSE: %.4f'% np.sqrt(sum((predictions_ARIMA-ts)**2)/len(ts)))
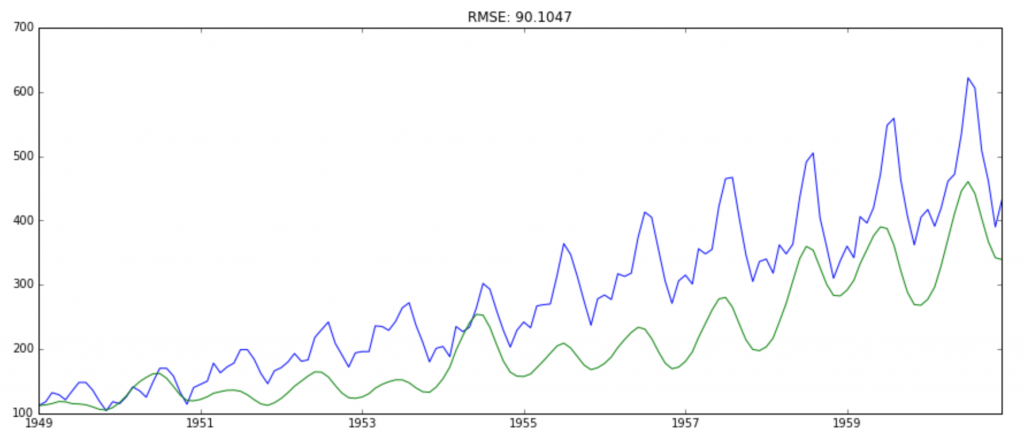
That’s all in Python. Well, let’s learn how to implement a time series forecast in R.
Time Series Forecast in R
Step 1: Reading data and calculating basic summary
Output
class(tsdata) "ts" > #Observations of the time series data > tsdata Jan Feb Mar Apr May Jun Jul Aug Sep Oct Nov Dec 1949 112 118 132 129 121 135 148 148 136 119 104 118 1950 115 126 141 135 125 149 170 170 158 133 114 140 1951 145 150 178 163 172 178 199 199 184 162 146 166 1952 171 180 193 181 183 218 230 242 209 191 172 194 1953 196 196 236 235 229 243 264 272 237 211 180 201 1954 204 188 235 227 234 264 302 293 259 229 203 229 1955 242 233 267 269 270 315 364 347 312 274 237 278 1956 284 277 317 313 318 374 413 405 355 306 271 306 1957 315 301 356 348 355 422 465 467 404 347 305 336 1958 340 318 362 348 363 435 491 505 404 359 310 337 1959 360 342 406 396 420 472 548 559 463 407 362 405 1960 417 391 419 461 472 535 622 606 508 461 390 432 > #Summary of the data and missi tsdata was converted to a data frame Data Frame Summary tsdata Dimensions: 144 x 1 Duplicates: 26 ---------------------------------------------------------------------------------------------------- No Variable Stats / Values Freqs (% of Valid) Graph Valid Missing ---- ---------- -------------------------- ----------------------- --------------------- -------- -- 1 tsdata Mean (sd) : 280.3 (120) 118 distinct values . : . 144 0 [ts] min < med < max: Start: 1949-01 : : . . : (100%) (0%) 104 < 265.5 < 622 End : 1960-12 : : : : : IQR (CV) : 180.5 (0.4) : : : : : : : : : : : : : : : . . ----------------------------------------------------------------------------------------------------
Step 2: Checking the cycle of Time Series Data and Plotting the Raw Data
Output
cycle(tsdata) Jan Feb Mar Apr May Jun Jul Aug Sep Oct Nov Dec 1949 1 2 3 4 5 6 7 8 9 10 11 12 1950 1 2 3 4 5 6 7 8 9 10 11 12 1951 1 2 3 4 5 6 7 8 9 10 11 12 1952 1 2 3 4 5 6 7 8 9 10 11 12 1953 1 2 3 4 5 6 7 8 9 10 11 12 1954 1 2 3 4 5 6 7 8 9 10 11 12 1955 1 2 3 4 5 6 7 8 9 10 11 12 1956 1 2 3 4 5 6 7 8 9 10 11 12 1957 1 2 3 4 5 6 7 8 9 10 11 12 1958 1 2 3 4 5 6 7 8 9 10 11 12 1959 1 2 3 4 5 6 7 8 9 10 11 12 1960 1 2 3 4 5 6 7 8 9 10 11 12

Step 3: Decomposing the time series data
Output

Step 4: Test the stationarity of data
Output
Augmented Dickey-Fuller Test data: tsdata Dickey-Fuller = -7.3186, Lag order = 5, p-value = 0.01 alternative hypothesis: stationary
the p-value is 0.01 which is <0.05, therefore, we reject the null hypothesis and hence time series is stationary.

The maximum lag is at 1 or 12 months, indicates a positive relationship with the 12-month cycle.
Autoplot the random time series observations from 7:138 which exclude the NA values

Step 5: Fitting the model
Output

Series: tsdata ARIMA(2,1,1)(0,1,0)[12] Coefficients: ar1 ar2 ma1 0.5960 0.2143 -0.9819 s.e. 0.0888 0.0880 0.0292 sigma^2 estimated as 132.3: log likelihood=-504.92 AIC=1017.85 AICc=1018.17 BIC=1029.35

Step 6: Forecasting
Output

Finally we have a forecast at the original scale. Not a very good forecast I would say but you got the idea right? Now, I leave it upto you to refine the methodology further and make a better solution.
Sample Projects
Now, its time to take the plunge and actually play with some other real datasets. So are you ready to take on the challenge? Test the techniques discussed in this post and accelerate your learning in Time Series Analysis with the following Practice Problems:
 | Practice Problem: Food Demand Forecasting Challenge | Forecast the demand of meals for a meal delivery company |
 | Practice Problem: Time Series Analyses | Forecast the passenger traffic for an intra-city rail system |
Conclusion
Through this article I have tried to give you a standard approach for solving time series problem. This couldn’t have come at a better time as today is our Mini DataHack which will challenge you to solve a similar problem. We’ve covered concepts of stationarity, how to take a time series closer to stationarity and finally forecasting the residuals. It was a long journey and I skipped some statistical details which I encourage you to refer using the suggested material. If you don’t want to copy-paste, you can download the iPython notebook with all the codes from my GitHub repository.
Frequently Asked Questions
A. The four main components of a time series are Trend, Seasonal, Cyclical, and Irregular.
A. Weather forecasts, stock market predictions, and predicting sales trends are some common examples of time series forecasts.
A. Time series forecasting is the technique of predicting future values by studying existing or past data.











Real thanks for a post which met my need
I'm glad you liked it :)
Thanks for great explanation related to timeseries. What is difference between holtwinters and arima forcast?
Holtwinters is double exponential smoothening method. ARIMA, forecasts by identifying p,d,q component of a series. Hope it helps.
Holt winters (at least the additive model) is a special case of arima model (a seasonal arima model). That would be an arima(p,d,q)(P,D,Q) where the second parentheses contains the seasonal effects. I would additionally recommend checking out any of Rob Hyndman's work on arima modeling, I find it to be very accessible.
Hi.. Thanks. for an informative article. I am eager to know on followings : a) how can we identify what should be nlags value to test with lag_acf = acf(ts_log_diff, nlags=20) lag_pacf = pacf(ts_log_diff, nlags=20, method='ols') b) How can we forecast for future time points (say 12 time points ahead). Can we use followings still ? predictions_ARIMA_log = pd.Series(ts_log.ix[0], index=ts_log.index) predictions_ARIMA_log = predictions_ARIMA_log.add(predictions_ARIMA_diff_cumsum,fill_value=0) ts_log is not available for future points. c) In one of the article ( A Complete Tutorial on Time Series Modeling in R,) referred by you , while performing adf says adf.test(diff(log(AirPassengers)), alternative="stationary", k=0) What is k , and how can we identify the value of k while performing the test.. while performing ARIMA says : fit <- arima(log(AirPassengers), c(0, 1, 1),seasonal = list(order = c(0, 1, 1), period = 12))) We can identify the (p,d,q) from ACF PACF plots . Please explain parameter seasonal = list(order = c(0, 1, 1) What values should we pass in seasonal parameter and how to identify it. It will be helpful if you guide on above.. Thanks in anticipation.
Hi Shan, Thanks for reaching out. Please find my responses below: a) So the ‘nlags’ doesn’t affect the output values. I just specifies how many values to display. So you can start with a small number and if you don’t find the crossing point within that, you can increase maximum upto the number of observations in data. b) ARIMA has a specific function for forecasting values. The ‘results_ARIMA’ variable here is of the type ‘ARIMAresults’ which has a ‘predict’ function. You can check the details as – http://statsmodels.sourceforge.net/devel/generated/statsmodels.tsa.arima_model.ARMAResults.predict.html#statsmodels.tsa.arima_model.ARMAResults.predict Please feel free to get back to me in case you face challenges in implementing this. You can also start a thread in the discussion forum which will allow more freedom of expression while discussing :) c) I’m not much experienced with R so let me read the code syntax. I’ll get back to you on this. Cheers!
Hi Shan, I guess you have started a separate discussion thread for your query 'c'. Lets continue the discussion there. For others who're reading this and interested in exploring further, please check out this link: http://discuss.analyticsvidhya.com/t/seasonal-parameter-in-arima-and-adf-test/7385/1 Cheers!
Thanks Aarshay for this write up. It is also recommended to not to go for combined models as p & q used together will nullify their impact on the model, hence, it is either a moving average or auto correlation along with differences, but here combined model has given the best results. Can you please correct my understanding around combined models.
I haven't read that p & q should not be combined. It's actually appears counter intuitive because if this was the case then ARIMA should not exist in the first place. Can you throw some light on why do you believe that they cancel out the effect of one another?
Hi! The article is the best available on Time Series with Python with great external links too for those who want to understand the stat behind also. I would like to request to please extend this article to predict out-of-sample data range also with different models to depict the better ones as you did for eliminating trend (taking rolling average and ewma). That will make it all fully fledged time-series article. Thanks in advance.
Hi Ayush! Thanks for your valuable feedback. Yes I think that component is necessary. But instead of extending this article, I'll probably write a separate post taking another case study. I'm a bit crunched for bandwidth but you can expect it sometime in this month. Stay tuned!
Thanks for the excellent article. I have 2 clarifications 1) In the Estimating & Eliminating Trend step, I have negative numbers. Could you please tell me what transformations could I apply. Log and Sqrt returns NAN? 2) Also, test_stationarity(ts_log_decompose,nlags=10) while executing specifies nlags not defined. Thanks in advance.
Hi Michael, Thanks for reaching out. Regarding your queries: 1. You can try scaling up your values and then applying transformations. Also, you might want to check if log transformation is actually required in your case. You can try a cube root as well. 2. Please remove the nlags argument and then run the code. I've updated the code above as well.
Nice article, you rarely see this range of models discussed in one place and in such a hands-on way. For anyone doing seasonal decomposition in Python, I'd like to shamelessly plug my `seasonal` package (PyPI or https://github.com/welch/seasonal) in addition to statsmodels seasonal_decompose. `seasonal` offers some richer and more robust detrending possibilities, and will also estimate your model's periodicity for you (convenient in a dev-ops setting with thousands of streams at hand). It also includes a robust periodogram for visualizing the periodicities in your data.
Thanks Will for sharing your library. It'll be helpful for everyone.
Can you please explain what is the dftest[0:4]?
the adfuller function returns a list with many values. I'm picking the first 4 using [0:4]. I've used the 5th value separately. You might want to print the dftest variable and you'll know.
Can we use this method for decimal data? Why the program gave me an error of "ValueError: You must specify a freq or x must be a pandas object with a timeseries index"?
I don't think it is a decimal error. Please check whether your index is a timeseries object.
Hi Aarshay Jain, One more question, When you fit model , you use ts_log as sampel, ie. model = ARIMA(ts_log, order=(2, 1, 2)) , but when you predict you use predict value as diff value : predictions_ARIMA_diff = pd.Series(results_ARIMA.fittedvalues, copy=True), is results_ARIMA.fittedvalues return log value or diff value? Thank you for your time.
actually while calling ARIMA I have set order = (2,1,2). Here the middle argument 1 means that ARIMA will automatically take a difference of 1 while making predictions.
What an excellent article on Time Series, more grease to your elbow. But the question is, is this method a package of analyzing Time Series related data or what? And can't we do the same on SPSS and have the same simple method as this? However, I have to commend you a lot for this wonderful presentation. God will continue to increase your knowledge.
Thanks Ayodeji! I'm not sure about SPSS and sorry I didn't get your questions - what do you mean "is this method a package of analyzing Time Series related data"? Please elaborate.
Hi Aarshay Jain I've tried the dickey-fuller test code with different dataset and then an error shown up like this: ValueError: too many values to unpack please give an advice thank you
please share the code..
Andrew, your are probably passing in a dataframe instead of a series, in the code Aarshay wrote up for the dftest. Specifically here: dftest = adfuller(timeseries.unstack(), autolag='AIC') note the .unstack() that I added -- transforming the df into a series -- when I also encountered the same error.
Hello, I am struggling on a question. Here, forecast is sowing upto 1960-12-01. Now based on the current measure, I want to forecast the upcoming years for example 1961-01-01 to 1965-12-01. How can I do this ?
Thanks Aarshay for this detailed and illustrative posts. one concern, the decomposition is not working for 12 months [of a single year] data. eg. in AirPassengers.csv if I take only the records of 1949 it fails to decompose giving below error: File "C:\anirban\install\Anaconda3\lib\site-packages\statsmodels\tsa\seasonal. py", line 88, in seasonal_decompose trend = convolution_filter(x, filt) File "C:\anirban\install\Anaconda3\lib\site-packages\statsmodels\tsa\filters\f iltertools.py", line 289, in convolution_filter result = signal.convolve(x, filt, mode='valid') File "C:\anirban\install\Anaconda3\lib\site-packages\scipy\signal\signaltools. py", line 470, in convolve return correlate(volume, kernel[slice_obj], mode) File "C:\anirban\install\Anaconda3\lib\site-packages\scipy\signal\signaltools. py", line 160, in correlate _check_valid_mode_shapes(in1.shape, in2.shape) File "C:\anirban\install\Anaconda3\lib\site-packages\scipy\signal\signaltools. py", line 72, in _check_valid_mode_shapes "in1 should have at least as many items as in2 in " ValueError: in1 should have at least as many items as in2 in every dimension for 'valid' mode. I think this is somehow related to the filter but not able to nail it since I am too novice. Please note - the code is exact replica of yours Any help will be appreciated, Thanks again :)
Great blog post, thanks for sharing this post. bawaseer ka ayurvedic ilaj
You are welcome :)
How to do the prediction for the future? start = len(ts) end = len(ts)+14 y_forecast = np.exp(results_ARIMA.predict(start, end)) This does not provide good results. Would you please expand your code and description to include one month ahead forecast?
Hi Thank You for sharing this post. i have one question: time series in pandas does only work with csv file because i want to forecast my database values for next 6 months. I did connect the python with mySQl database. i.e i have data in python with dataset not in csv file.So how can i used time series forecasting method. If you provide me code it will be huge help for me.
this problem is done.... by using data = pd.read_sql_query(cur,con).
In Dicket-fuller test my came Results of Dickey-Fuller Test: Test Statistic -2.287864 p-value 0.175912 #Lags Used 11.000000 Number of Observations Used 215.000000 Critical Value (1%) -3.461136 Critical Value (10%) -2.573986 Critical Value (5%) -2.875079 dtype: float64 My p value is so less? Its means my data is not normal ox not not suited to this model?
This problem is also done.
If test static (-2.287864) is greater than critical value (-3.46, -2.57, -2.87) then we can't reject the null hypothesis, the series is stationary. That said it is still non-stationary. If you increase the i value in ARIMA model, perhaps above condition may meet and you may get the good forecast values.
Hi Aarshay, I really enjoyed this but running on python 3, I've encountered a couple errors on the last portion. "plt.title('RSS: %.4f'% sum((results_MA.fittedvalues-ts_log_diff)**2)) pandas\tslib.pyx in pandas.tslib.Timestamp.__radd__ (pandas\tslib.c:14048)() pandas\tslib.pyx in pandas.tslib._Timestamp.__add__ (pandas\tslib.c:19022)() ValueError: Cannot add integral value to Timestamp without offset.' Googling around it seems that its a bug in statsmodel but if I was wondering perhaps if you or someone else ported it to python 3? Thanks
Thank you for this post. I find error in model = ARIMA(ts_log, order=(2, 1, 0)) and i unable to find the error.Please me
thank you for this example. i have one problem. When i tried to put model in my program its said ValueError: Given a pandas object and the index does not contain dates but in my dataset date is there. data = pd.read_sql_query(cur,con, index_col='datum', coerce_float=True, params=None) I dont know what is problem with this?
I still prefer gretl for building time series and econometric models easy to use its an open source just download and go
Hi, thank you for your sharing. I am using this model to predict play number of a song. When I input data with 'data = pd.read_csv('00play.csv', parse_dates='data', index_col='data',date_parser=dateparse)' There are some error 'TypeError: Only booleans, lists, and dictionaries are accepted for the 'parse_dates' parameter' if I delete this parameter parse_dates, is there any influence? Using data without parameter parse_dates, when making seasonal_decompose, another error is 'ValueError: freq D not understood. Please report if you think this in error.' please give an advice thank you
hi can you give me an idea in case of multiple time series forecasting
really liked this post. Thank you very much for sharing.
How to deal with the tendency of irregular time series data(data with different time interval)?
Hi, This is a very good blog and very useful. I could follow the entire process. But I did not understand how to forecast for next 12 months from the last value. In the current case the last value is 1960-12, I need to forecast till 1961-12 (12 values). How can I do that in the following code? It would be great if you kindly add that process and update this article. predictions_ARIMA_log = pd.Series(ts_log.ix[0], index=ts_log.index) predictions_ARIMA_log = predictions_ARIMA_log.add(predictions_ARIMA_diff_cumsum,fill_value=0)
Hi Aarshay, First of all thanks for this brilliant post. I am following a similar approach for forecasting a minute's data using previous hours data. I am using forecast function in statsmodels along with ARIMA model. Calculating the P, Q and D using the approach you mentioned in your post. However, I am facing a few problems: 1. At times the ARIMA throws an error for AR or MA parameter . 2. ARIMA in python takes a lot of time. Similar code in R takes less than 30 minutes for forecasting a months data. Am I missing something or ARIMA in python is inherently slow? 3. I get MLE not converging Warning almost every-time, why is that so. 4. ARIMA does not allow D value more than two, however, at times adfuller results in d value more than two. What should be done in this case. Looking forward to your suggestions. Thanks, Aaditya
Hi Arshay, This is very useful article. I got a small doubt about forecasting values. How can I get the forecast values from the following code? Suppose I want to print for next 1 year, how can I do that? Thanks, Satya predictions_arima_log = pd.Series(ts_log.ix[0], index=ts_log.index) predictions_arima_log = predictions_arima_log.add(predictions_arima_diff_cumsum,fill_value=0)
Thank you for such a detailed post. I was wondering what if the data was in Country-level? How can we deal with such time series data then?
For this code line: data = pd.read_csv('AirPassengers.csv', parse_dates='Month', index_col='Month',date_parser=dateparse) Does it work? I got error message in my Anaconda Python 2.7 because Python can't identify 'Month' as a list of Month column value for parameter parse_dates, so I changed to ['Month'], It works. Could anyone confirm it in Python 3? Thanks.
"ValueError: Cannot add integral value to Timestamp without offset." i keep getting this error whenever I use the ARIMA function and I was wondering if you could tell me what this means and how i could fix it. Im using the same data and steps as the example above.
Thanks for this great article, it greatly helped me get started with time series forecasting. What would be the additional steps if you wanted to make a more accurate forecast?
Really nice post, My question is how would different would the second part of the problem be if you were to use decomposing instead of differecing for forecasting the time-series?
Can someone please explain while creating ARIMA models you are using ts_log ( just a log time series) but while calculating RSS you are using ts_log_diff . Am i missing something here ?
Hey I'm a newbie in machine learning and wanted sort out an issue: What type of problems can be classified under time forecasting problem. Many tutorials begin with predicting stock prices for next few days, so is it a time forecast problem. Also is the Bike sharing Demand question from Kaggle a part of time forecasting question as we are given the demand for some dates and we need to predict demand for upcoming days.
How to select which model is better one for our data? Is there any parameters in data to select models ?
This is literally the BEST article I've ever seen on time-series analysis with Python. Very well explained. I wish the statsmodels documentation was this good (they give you the tools but don't show you how to use them!). I am very confused about ACF and PACF and how to read the charts to determine the proper P an Q. You concluded that p and q are both 2 and you mention "upper confidence level". I don't see the lines crossing the upper-confidence level dashed line at point 2 in ACF or PACF. Is this a typo? If not a typo, can you explain?
I wonder what your thoughts are on doing a decomposition, then performing ARIMA forecasting on each component (trend, seasonality, residual), then re-scaling back. Is this a sound method/approach? I did this and the prediction line looks like what I'd expect. I'm just wondering if this is a common practice.
Hi Aarshey.. great article. I have tested the code and working fine, however, I am not getting the years in X axis, I tried different date parse methods, but no luck. How did you get year values in X axis where as parse method converting Month column as string in %Y-%m-%d format?
I got confused on many points: 1- we do many transformations to get stationarity data and every transformation we get data with good stationarity and on the example, you got the best stationary after applying the Decomposing, then why did you use the ts_log_diff and ts_log data with ACF,PACF and ARIMA instead of using the Decomposing data !? 2- I did see many styles for ACF and PACF one like continuous graph and another one like pins, which one I should go for it? 3- what is the best and easiest way to detect AR and MA by ACF and PACF? some tutorials mention about every ARIMA model has a special ACF and PACF pattern and others mention about the intersection between the lags and the confidence upper line! 4-is there any way to automate the step of getting the AR and MA instead of trying to investigate the ACF and PACF plots?
thanks alot for the information, i learned a ton. Im just a little confused now that i have this model how to use it to predict the next point in time
Hi I am getting this error when I am writing the following codes, can anyone help? date1= lambda dates: pd.datetime.strptime(dates, '%Y-%m') dataset= pd.read_csv('AirPassangers.csv', parse_dates='Month', index_col='Month',date_parser=date1) This is what I am getting: ======== date1= lambda dates: pd.datetime.strptime(dates, '%Y-%m-%d') dataset= pd.read_csv('AirPassangers.csv', parse_dates='Month', index_col='Month',date_parser=date1) Traceback (most recent call last): File "", line 1, in dataset= pd.read_csv('AirPassangers.csv', parse_dates='Month', index_col='Month',date_parser=date1) File "C:\Users\dwiti.b\AppData\Local\Continuum\Anaconda2\lib\site-packages\pandas\io\parsers.py", line 562, in parser_f return _read(filepath_or_buffer, kwds) File "C:\Users\dwiti.b\AppData\Local\Continuum\Anaconda2\lib\site-packages\pandas\io\parsers.py", line 315, in _read parser = TextFileReader(filepath_or_buffer, **kwds) File "C:\Users\dwiti.b\AppData\Local\Continuum\Anaconda2\lib\site-packages\pandas\io\parsers.py", line 645, in __init__ self._make_engine(self.engine) File "C:\Users\dwiti.b\AppData\Local\Continuum\Anaconda2\lib\site-packages\pandas\io\parsers.py", line 799, in _make_engine self._engine = CParserWrapper(self.f, **self.options) File "C:\Users\dwiti.b\AppData\Local\Continuum\Anaconda2\lib\site-packages\pandas\io\parsers.py", line 1202, in __init__ ParserBase.__init__(self, kwds) File "C:\Users\dwiti.b\AppData\Local\Continuum\Anaconda2\lib\site-packages\pandas\io\parsers.py", line 893, in __init__ kwds.pop('parse_dates', False)) File "C:\Users\dwiti.b\AppData\Local\Continuum\Anaconda2\lib\site-packages\pandas\io\parsers.py", line 873, in _validate_parse_dates_arg raise TypeError(msg) TypeError: Only booleans, lists, and dictionaries are accepted for the 'parse_dates' parameter
thank you for this post. however do you have any tutorials on stock price prediction using artificial neural networks?
This is not a complete guide. This can be something to get you started. Time series analysis is not that limited.
Comments are Closed