DeepSeek Math V2 Guide: Smarter AI for Real Math

If you’ve been following the AI space lately, you’ve probably noticed something big: people don’t just care what an AI answers anymore, they care how it reaches that answer. And that’s exactly where DeepSeek Math V2 steps in. It’s an open-source model built specifically for real mathematical reasoning.

In this guide, I’ll walk you through what DeepSeek Math V2 is, why everyone is talking about its generator-verifier system, and how this model manages to solve complex proofs while checking its own work like a strict math teacher. If you’re curious about how AI is finally getting good at formal math, keep reading.

What is DeepSeek Math V2? 

DeepSeek Math V2 is DeepSeek-AI’s newest open-source LLM built specifically for mathematical reasoning and theorem proving. Launched at the end of 2025, it marks a big shift from AI models that simply return final answers to ones that actually show their work and justify every step.

What makes it special is its two-model generator–verifier setup. One model writes the proof, and the second model checks each step like a logic inspector. So instead of just solving a problem, DeepSeek Math V2 also evaluates whether its own reasoning makes sense. The team trained it with reinforcement learning, rewarding not just correct answers but clean, rigorous derivations.

And the results speak for themselves. DeepSeek Math V2 performs at the top level in major math competitions, scoring around 83.3% at IMO 2025 and 98.3% on the Putnam 2024. It surpasses earlier open models and comes surprisingly close to the best proprietary systems out there.

Key Features of DeepSeek Math V2 

• Massive scale: With 685B parameters built on DeepSeek-V3.2-ExpBase, the model handles extremely long proofs using multiple numeric formats (BF16, F8_E4M3, F32) and sparse attention for efficient computation.
• Self-verification: A dedicated verifier checks every proof step for logical consistency. If a step is wrong or a theorem is misapplied, the system flags it and the generator is retrained to avoid repeating the mistake. This feedback loop forces the model to refine its reasoning.
• Reinforcement training: The model was trained on mathematical literature and synthetic problems, then improved through proof-based reinforcement learning. The generator proposes solutions, the verifier scores them, and harder proofs yield stronger rewards, pushing the model toward deeper and more accurate derivations.
• Open source and accessible: The weights are released under Apache 2.0 and available on Hugging Face and GitHub. You can also try DeepSeek Math V2 directly through the free DeepSeek Chat interface, which supports non-commercial research and educational use.

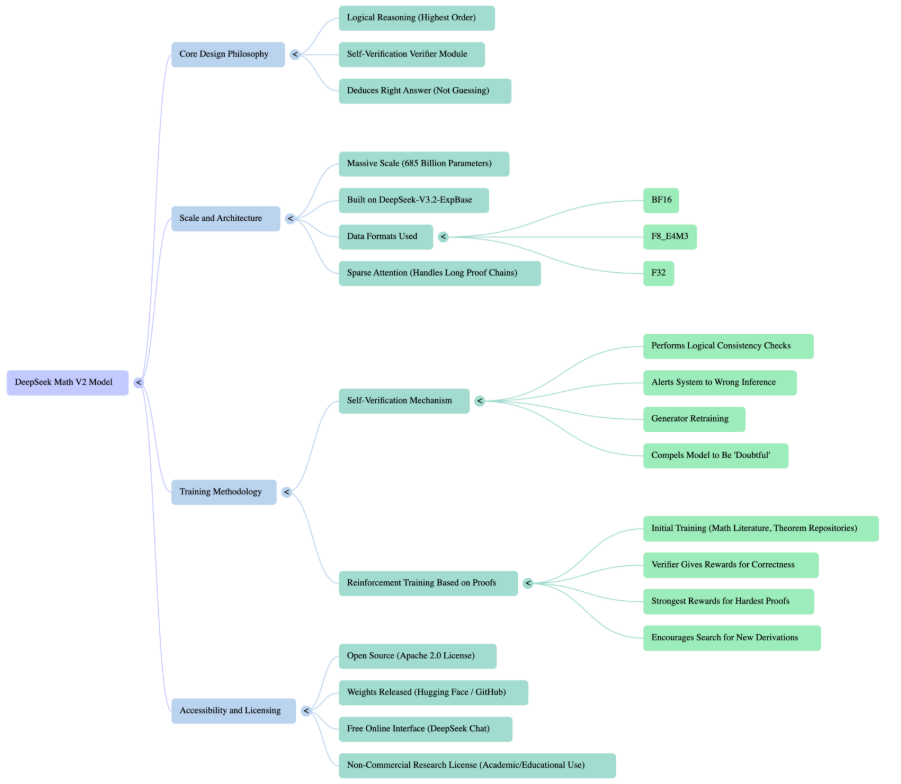
The Two-Model Architecture of DeepSeek Math V2

DeepSeek Math V2’s architecture presents two principal components that interact with each other: 

• Proof Generator: This large transformer LLM (DeepSeek-V3.2-Exp-Base) is responsible for creating step-by-step mathematical proofs based on the problem statement. 

• Proof Verifier: Although it is a smaller network, it is an extensively trained one that represents every proof with logical steps (for example, via an abstract syntax tree) and carries out the application of mathematical rules on them. It indicates the inconsistencies in the reasoning or the invalid manipulations that are not termed as ‘words’ and assigns a “score” to each proof. 

Training happens in two stages. First, the verifier is trained on known correct and incorrect proofs. Then the generator is trained with the verifier acting as its reward model. Every time the generator produces a proof, the verifier scores it. Wrong steps get penalized, fully correct proofs get rewarded, and over time the generator learns to produce clean, valid derivations.

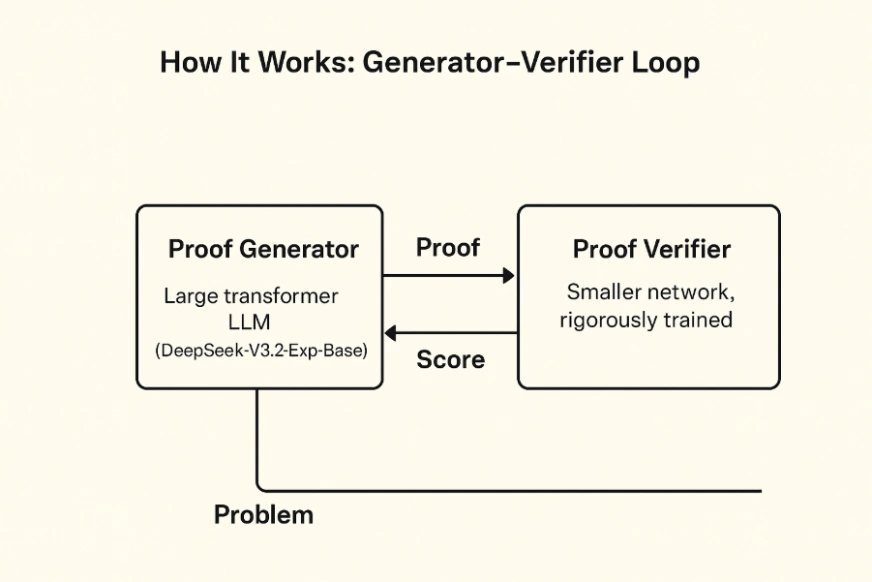
Multi-Pass Verification and Search

As the generator improves and starts producing more difficult proofs, the verifier receives extra compute such as additional search passes to catch subtler mistakes. This creates a moving target where the verifier always stays slightly ahead, pushing the generator to improve continuously.

During normal operation, the model also uses a multi-pass inference process. It generates many candidate proof drafts, and the verifier checks each one. DeepSeek Math V2 can branch in an MCTS-style search where it explores different proof paths, removes the ones with low verifier scores, and iterates on the promising ones. In simple terms, it keeps rewriting its work until the verifier approves it.

def generate_verified_proof(problem):
    root = initialize_state(problem)
    while not root.is_complete():
        children = expand(root, generator)
        for child in children:
            score = verifier.evaluate(child.proof_step)
            if score < THRESHOLD:
                prune(child)
        root = select_best(children)
    return root.full_proof

DeepSeek Math V2 ensures that every answer comes with clear, step-by-step reasoning, thanks to its mix of generation and real-time verification. This is a major upgrade from models that only aim for the final answer without showing how they reached it.

How to Access DeepSeek Math 2?

The model weights and code are publicly available under an Apache 2.0 license (DeepSeek additionally mentions a non-commercial research-friendly license). To try it out, you can:  

• Download from Hugging Face: The model is hosted on Hugging Face deepseek-ai/DeepSeekMath-V2 . Using the Hugging Face Transformers library, one can load the model and tokenizer. Keep in mind it’s huge, you’ll need at least several high-end GPUs (the repo recommends 8×A100) or TPU pods for inference. 

• DeepSeek Chat interface: If you don’t have massive compute, DeepSeek offers a free web demo at chat.deepseek.com . This “Chat with DeepSeek AI” allows interactive prompting (including math queries) without setup. It’s an easy way to see the model’s output on sample problems.  

• APIs and integration: You can deploy the model via any standard serving framework (e.g. DeepSeek’s GitHub has code for multi-pass inference). Tools like Apidog or FastAPI can help wrap the model in an API. For example, one might create an endpoint /solve-proof that takes a problem text and returns the model’s proof and verifier comments. 

Now, let’s try the model out!

Task 1: Generate a Step-by-Step Proof

Prerequisites: 

1. GPU with at least 40GB VRAM (e.g., A100, H100, or similar). 
2. Python environment (Python 3.10+) 
3. Install latest versions of: 

pip install transformers accelerate bitsandbytes torch –upgrade 

Step 1: Choose a Math Problem 

For this hands-on, we’ll be using the following problem which is very common in math olympiads: 

Let a, b, c be positive real numbers such that a + b + c = 1. Prove that a² + b² + c² ≥ 1/3.

Step 2: Python script to run the Model 

from transformers import AutoTokenizer, AutoModelForCausalLM
import torch

# Load model and tokenizer
model_id = "deepseek-ai/DeepSeek-Math-V2"
tokenizer = AutoTokenizer.from_pretrained(model_id, trust_remote_code=True)
model = AutoModelForCausalLM.from_pretrained(
    model_id,
    torch_dtype=torch.bfloat16,
    device_map="auto",
    trust_remote_code=True
)

# Prompt
prompt = """You are DeepSeek-Math-V2, a competition-level mathematical reasoning model.
Solve the following problem step by step. Provide a complete and rigorous proof.
Problem: Let a, b, c be positive real numbers such that a + b + c = 1. Prove that a² + b² + c² ≥ 1/3.
Solution:"""

# Tokenize and generate
inputs = tokenizer(prompt, return_tensors="pt").to(model.device)
outputs = model.generate(
    **inputs,
    max_new_tokens=512,
    temperature=0.2,
    top_p=0.95,
    do_sample=True
)

# Decode and print result
output_text = tokenizer.decode(outputs[0], skip_special_tokens=True)
print("\n=== Proof Output ===\n")
print(output_text)

# Step 3: Run the script
# In your terminal, run the following command:
# python deepseek_math_demo.py

Or if you require then you can test it on the web interface as well. 

Output:  

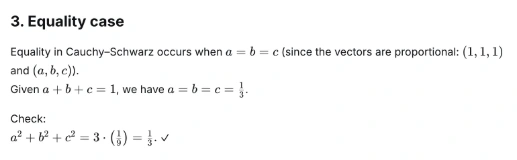
Task 2: Check the Correctness of a Mathematical Proof 

In this task, we will feed DeepSeek Math V2 a flawed math proof and ask its Verifier component to critique and validate the reasoning. It will basically show one of the most important features of DeepSeek Math V2, self-verification. 

Step 1: Define the Problem:

Step 2: Add the Verifier Prompt code:

from transformers import AutoTokenizer, AutoModelForCausalLM
import torch

model_id = "deepseek-ai/DeepSeek-Math-V2"
tokenizer = AutoTokenizer.from_pretrained(model_id, trust_remote_code=True)
model = AutoModelForCausalLM.from_pretrained(
    model_id,
    torch_dtype=torch.bfloat16,
    device_map="auto",
    trust_remote_code=True
)

# Incorrect proof for DeepSeek to verify
incorrect_proof = """
Claim: For all real numbers x, x^2 + 2x + 5 ≥ 0.
Proof: Since x^2 is always positive and 2x + 5 is always positive, their sum is always positive. Hence x^2 + 2x + 5 ≥ 0 for all real x.
"""

prompt = f"""You are the DeepSeek Math V2 Verifier.
Your task is to critically analyze the following proof, identify incorrect reasoning,
and provide a corrected, rigorous explanation.
Proof to verify:
{incorrect_proof}
Please provide:
1. Whether the proof is correct or incorrect.
2. Which steps contain mistakes.
3. A corrected proof.
"""

inputs = tokenizer(prompt, return_tensors="pt").to(model.device)
outputs = model.generate(
    **inputs,
    max_new_tokens=600,
    temperature=0.2,
    top_p=0.95,
    do_sample=True
)

print("\n=== Verifier Output ===\n")
print(tokenizer.decode(outputs[0], skip_special_tokens=True))

# Step 3: Run the script
# In your terminal, run the following command:
# python deepseek_verifier_demo.py 

Output: 

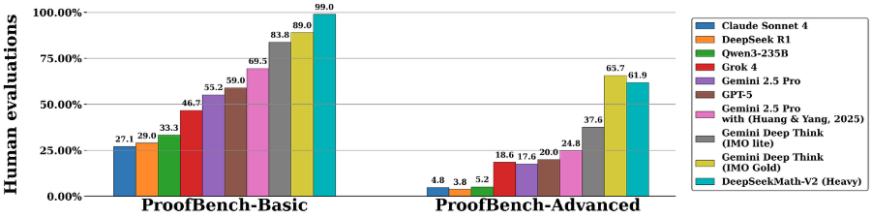
Performance and Benchmarks 

DeepSeek Math V2 delivers standout results across major math benchmarks:

• International Math Olympiad (IMO) 2025: Scored around 83.3 percent by fully solving problems 1 to 5 and partially solving problem 6. This matches top closed-source systems, even before its official contest entry.
• Canadian Math Olympiad (CMO) 2024: Scored about 73.8 percent by fully solving 4 of 6 problems and partially solving the rest.
• Putnam Exam 2024: Achieved 98.3 percent (118 out of 120 points) under scaled compute, only missing partial credit on the toughest questions.
• ProofBench (DeepMind): Received about 99 percent approval on basic proofs and 62 percent on advanced proofs, outperforming GPT-4, Claude 4, and Gemini on structured reasoning.

In side-by-side comparisons, DeepSeek Math V2 consistently beats leading models on proof accuracy by 15 to 20 percent. Many models still guess or skip steps, while DeepSeek’s strict verification loop reduces error rates significantly, with reports showing up to 40 percent fewer reasoning mistakes than speed-focused systems.

Applications and Significance 

DeepSeek Math V2 is not just strong in competitions. It pushes AI closer to formal verification by treating every problem as a proof-checking task. Here are the main ways it can be used:

• Education and tutoring: It can grade math assignments, check student proofs, and provide step-by-step hints or practice problems.
• Research assistance: Useful for exploring early ideas, spotting weak reasoning, and generating new approaches in areas like cryptography and number theory.
• Theorem-proving systems: It can support tools like Lean or Coq by helping translate natural-language reasoning into formal proofs.
• Quality control: It can verify complex calculations in fields such as aerospace, cryptography, and algorithm design where accuracy is critical.

Also Read:

• How DeepSeek Trained AI 30 Times Cheaper?
• DeepSeek’s New OCR Compresses Documents By 10x
• DeepSeek-V3.2-Exp: 50% Cheaper, 3x Faster, Maximum Value

Conclusion 

DeepSeek Math V2 is a powerful tool among AI’s math-related tasks. It connects a vast transformer backbone with new proof-checking loops, achieves record scores in contests, and is made available to the community for free. The development of AI has always been the case in DeepSeek Math V2 that self-verifying is the core of deep thinking, not only of larger models or data.

Try it out today and let me know your thoughts in the comment section below!