Linear Algebra for Data Science With Python
This article was published as a part of the Data Science Blogathon.
Introduction
Linear Algebra, a branch of mathematics, is very much useful in Data Science. We can mathematically operate on large amounts of data by using Linear Algebra.
Most algorithms used in ML use Linear Algebra, especially matrices. As most of the data is represented in matrix form.
Now that we know how L. A is used, let’s just get into it!!! We’ll start with the basics — VECTORS
Vectors
[1] is the definition that is available on Wikipedia. Most people understand it, but to make it simpler you can just say that a vector is:“In mathematics and physics, vector is a term that refers colloquially to some quantities that cannot be expressed by a single number, or to elements of some vector spaces.“ [1]
It is a term that refers to a quantity that has both magnitude and direction.
It is the fundamental building block of linear algebra. Now if you take a look at the definition that is from the Wiki you can see that — quantities cannot be expressed by a single number. Meaning, that they have a dimension and it can be anything.
A dimensionality of a vector is determined by the number of numerical elements in that vector.
Example: A vector with 4 elements will have a dimensionality of four.
The magnitude of a vector is calculated by using the formula:
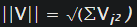 Applying Vectors using Python
Applying Vectors using PythonNumpy arrays are n-dimensional array data structures that can be used to represent both vectors and matrices.
import numpy as np
v = np.array([1,2,3,4,5]) #vectorBasic Vector Operations
Scalar Multiplication with Python:
Python Code:
Vector Addition and Subtraction with Python:
import numpy as np
A = np.array([1,2,3,4]) #vector1
B = np.array([-4,-3, -2, -1]) #vector2
print(A+B) #vector Addition
print(A-B) #vector SubtractionVector Dot Products:
Dot product takes 2 equal dimension vectors and returns a single scalar value by summing the products of vectors corresponding components.
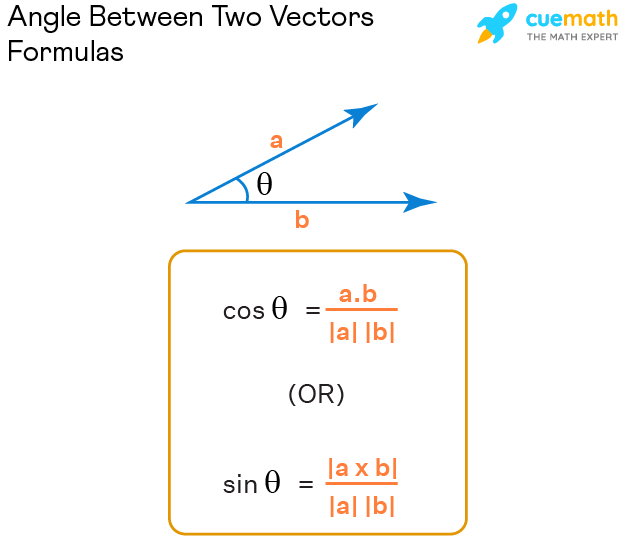
The formula is

The dot product is both commutative and distributive.
a.b = b.c
a.(b+c) = a.b + a.c
The resulting scalar value represents how much one vector goes into the other.
If two vectors are perpendicular, then their dot product is 0, as neither goes into the other. The dot product can also be used to find the magnitude of a vector and the angle between two vectors.
Example for dot product using python:
import numpy as np
A = np.array([1,2,3,4]) #vector1
B = np.array([-4,-3, -2, -1]) #vector2
print(np.dot(A, B)) #dot productMatrices
It’s a quantity with m rows and n columns of data. We can combine multiple vectors into a matrix for each that matrix is one of the vectors. Matrices are helpful because they allow us to perform operations on large amounts of data, such as representing entire systems of equations in a matrix quantity. We can even access the elements by using the row and column numbers.
Example for matrix using python
import numpy as np A = np.array([[1,2],[3,4]]) #matrix print(A[1,1]) #accessing the elements of the matrix A
Matrix Operations
Matrix Addition and Subtraction With Python
import numpy as np A = np.array([[1,2],[3,4]]) #matrix1 B = np.array([[-3,-2],[-4,-5]]) #matrix2 print(A+B) #Addition print(A-B) #Subtraction
Matrix Multiplication
It works by computing the dot product between each row of the first matrix and each column of the 2nd matrix. If the matrices are having then dimensions m x n and k x l. If n = k, only then are we able to perform the multiplication.
Example with Python
There are two ways to do this. One is using the “@” and the other is to use the .matmul() from numpy module
import numpy as np A = np.array([[1,2],[3,4]]) #matrix1 B = np.array([[-3,-2],[-4,-5]]) #matrix2 print(np.matmul(A, B)) print(A@B)
Both the print statements give the same result.
Special Matrices
There are particularly 3 types of special matrices.
Identity Matrix
A square matrix with diagonal elements as 1 and remaining as 0. Any matrix multiplied with the identity matrix is itself.
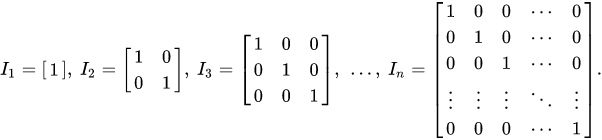
Image from Wikipedia
In python, we can create an identity matrix by using the
.eye() method from numpy import numpy as np identity = np.eye(4) #creates a 4x4 matrixTranspose Matrix
It is computed by swapping the rows and cols of a matrix. It is denoted by “T”
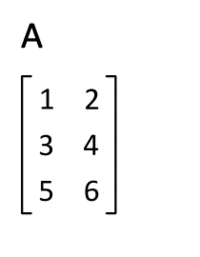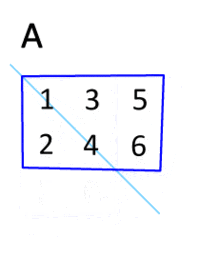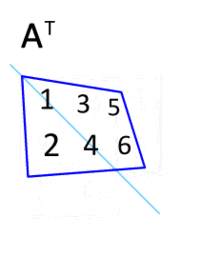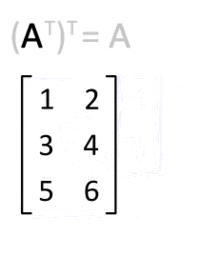
Image from Wikipedia
In python, we can use .T to transpose the matrix.
import numpy as np A = np.array([[1,2],[3,4]]) #matrix A_trans = A.T
Permutation Matrix
It’s a square matrix that allows us to flip rows and columns of a separate matrix. It’s kind of similar to identity where every element is 0 except for one element in a row which is 1.
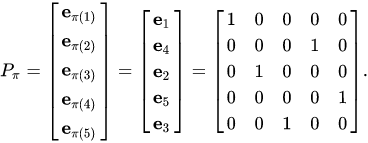
Image from Wikipedia
To flip rows in a matrix A we multiply a permutation matrix P on the left (PA). To flip cols, we multiply a permutation matrix P on the right (AP)
Click here to know how to implement this in python.
Linear System in Matrix Form
An extremely useful application of matrices is for solving systems of linear equations.
Let’s take a look at an example.
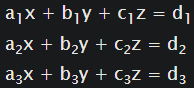
We can solve such linear systems by using Numpy’s linalg submodule.
Example:
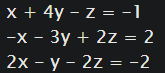
We converted the above linear equation system into matrices.
A = np.array([[1,4,-1],[-1,-3,-2],[2, -1, -2]])
b = np.array([-1,2,-2])
x, y, z = np.linalg.solve(A, b)Inverse Matrix
[2] Wikipedia“In linear algebra, an n-by-n square matrix A is called invertible (also nonsingular or nondegenerate), if there exists an n-by-n square matrix B such that AB = BA = I” [2]
As mentioned above the product of the inverse of a matrix and itself is identity. Not all matrices have an inverse. Those who don’t have an inverse are called singular matrices.
Example with Python:
import numpy as np
A = np.array([[1,2],[3,4]])
print(np.linalg.inv(A))Miscellaneous
We can create a matrix or vector consisting of zeros by using the zeros() of NumPy
Example:
import numpy as np
print(np.zeros((3,2)) #prints a matrix of dimensions 3x2- “norm” of a matrix can be found by using Numpy’s linalg submodule.
Example:
import numpy as np
A = np.array([2,-4,1])
A_norm = np.linalg.norm(A) #gives 4.5825
In this blog we learned:
- Definition of Matrix
- How to implement them in python
- Different matrix Operations and their implementation with Python
- Special Matrices and their implementation with Python
That’s it for the blog guys. I hope you found this helpful if you did follow me on LinkedIn.
If you like my work, you can buy me a cup of coffee: dataguy6@ybl
The media shown in this article is not owned by Analytics Vidhya and is used at the Author’s discretion.











