Dummy Variable Trap in Machine Learning Explained Simply

In machine learning with categorical data, it is common to encode the categories as dummy variables (sometimes called one hot encoding) to encode categories as numerical values. This is a significant step since there are many algorithms that do not operate on other things other than numbers like linear regression. Nevertheless, there is one of the mistakes that beginners are likely to make. It is referred to as the dummy variable trap. This problem is better understood at the outset to avoid the confounding of model outcomes and other unwarranted flaws.

What Are Dummy Variables and Why are They Important? 

Most machine learning algorithms are only able to accept numerical input. This poses a problem in case our data is about red, blue, and green or any other category. Dummy variable helps to resolve this issue by transforming categorical data into numbers. 

A binary variable is a dummy variable and takes 0 or 1. The use of a dummy variable corresponds to a single category and whether the category is present or not with regards to a particular data point. 

As a case in point, consider a dataset that has a nominal factor known as Color, which can assume three values, i.e., Red, Green, and Blue. To transform this feature into numbers we construct three new columns: 

• Color_Red 
• Color_Green 
• Color_Blue 

The value of each of these columns will be 1 in one row and 0 in the remaining rows. 

• Assuming a Red data point, then Color Red is 1 and the rest of the two columns are 0. 
• In case of the color Green, then the color of Green is 1 and the rest are 0. 
• When it is Blue, then Color-Blue = 1 and Color-Other = 0. 

This is because, the approach enables models to learn categorical data without misleading information. As an example, coding Red = 1, Green = 2 and Blue = 3 would falsely indicate that Blue is more than Green and Green is more than Red. Most models would consider these numbers to have an order to them which is not what we desire. 

Succinctly, dummy variables are a safe and clean means of incorporating categorical variables into machine learning models that need numerical data. 

What Is the Dummy Variable Trap?

One of the most common issues that arises while encoding categorical variables is the dummy variable trap. This problem occurs when all categories of a single feature are converted into dummy variables and an intercept term is included in the model. While this encoding may look correct at first glance, it introduces perfect multicollinearity, meaning that some of the variables carry redundant information.

In practical terms, the dummy variable trap happens when one dummy variable can be completely predicted using the others. Since each observation belongs to exactly one category, the dummy variables for that feature always sum to one. This creates a linear dependency between the columns, violating the assumption that predictors should be independent.

Dummy Variable Trap Explained with a Categorical Feature

To understand this more clearly, consider a categorical feature such as Marital Status with three categories: Single, Married, and Divorced. If we create one dummy variable for each category, every row in the dataset will contain exactly one value of 1 and two values of 0. This leads to the relationship:

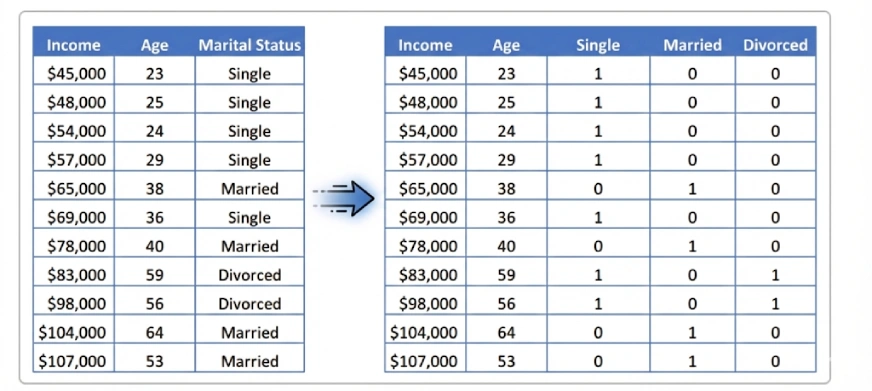
Single + Married + Divorced = 1

Since this relationship is unconditionally true, one of the columns is redundant. When one is neither a Single nor Married, then he must be Divorced. The other columns can give the same conclusion. The error is the dummy variable trap. The use of dummy variables to represent each category, and a constant term, creates perfect multicollinearity.

In this case, there are possibilities of some of the dummy variables being perfectly correlated with others. An example of this is two dummy columns which move in a fixed opposite direction with one 1 when the other is 0. This implies that they are carrying duplicating information. Because of this, the model cannot ascertain a distinct impact of every variable.

Mathematically, it happens that the feature matrix is not full rank, that is, they are singular. When that occurs then the linear regression cannot calculate a unique model coefficient solution.

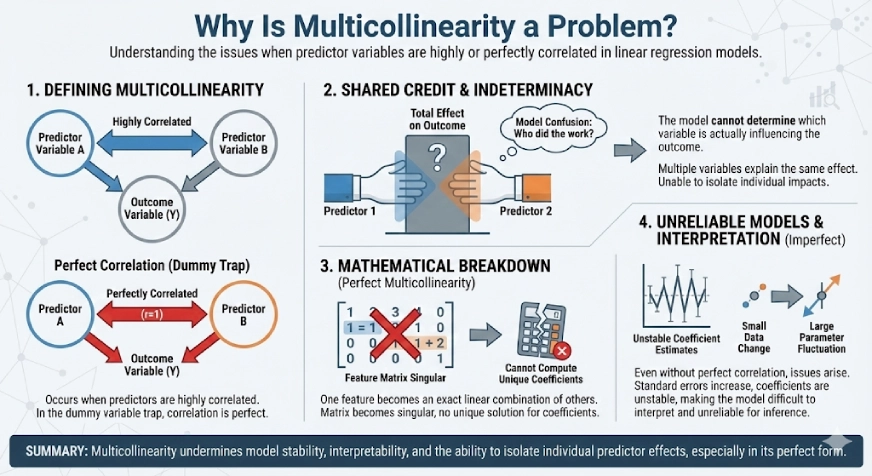
Why Is Multicollinearity a Problem?

Multicollinearity occurs when two or more predictor variables are highly correlated with each other. In the case of the dummy variable trap, this correlation is perfect, which makes it especially problematic for linear regression models.

When predictors are perfectly correlated, the model cannot determine which variable is actually influencing the outcome. Multiple variables end up explaining the same effect, similar to giving credit for the same work to more than one person. As a result, the model loses the ability to isolate the individual impact of each predictor.

In situations of perfect multicollinearity, the mathematics behind linear regression breaks down. One feature becomes an exact linear combination of others, making the feature matrix singular. Because of this, the model cannot compute a unique set of coefficients, and there is no single “correct” solution.

Even when multicollinearity is not perfect, it can still cause serious issues. Coefficient estimates become unstable, standard errors increase, and small changes in the data can lead to large fluctuations in the model parameters. This makes the model difficult to interpret and unreliable for inference.

Example: Dummy Variable Trap in Action 

To put this point in context, let us consider a basic example. 

Let us consider a small set of ice cream sales. One of the categorical features is Flavor, and the other numeric target is Sales. The data set consists of three flavors, namely Chocolate, Vanilla and Strawberry. 

We start with the creation of a pandas DataFrame. 

import pandas as pd 
 
# Sample dataset 
df = pd.DataFrame({ 
    'Flavor': ['Chocolate', 'Chocolate', 'Vanilla', 'Vanilla', 'Strawberry', 'Strawberry'], 
    'Sales': [15, 15, 12, 12, 10, 10] 
}) 
 
print(df 

Output:

   Flavor        Sales
0  Chocolate        15
1  Chocolate        15
2  Vanilla          12
3  Vanilla          12
4  Strawberry       10
5  Strawberry       10

This produces a simple table. Each flavor appears twice. Each has the same sales value. 

We then change the Flavor column into dummy variables. To illustrate the problem of dummy variables, we will artificially generate a dummy column in each category. 

# Create dummy variables for all categories 
dummies_all = pd.get_dummies(df['Flavor'], drop_first=False) 
 
print(dummies_all) 

Output:

   Chocolate   Strawberry   Vanilla
0      True        False      False
1      True        False      False
2     False        False       True
3     False        False       True
4     False         True      False
5     False         True      False

This results in three new columns.

• Chocolate
• Vanilla
• Strawberry

The number of 0s and 1s is limited to each column. 

A column such as Chocolate would be 1 in the event of Chocolate flavor. The others are 0. The same argument goes through on the other flavors. 

Now observe something of significance. The dummy values in each row are always equal to 1. 

FlavorChocolate + FlavorVanilla + FlavorStrawberry = 1 

This implies that there is an unnecessary column. Assuming that there are two columns with 0, the third one must be 1. That additional column does not provide any new information to the model. 

It is the dummy variable trap. If we add all the three dummy variables and neglecting to add an intercept term to a regression equation, we achieve perfect multicollinearity. The model is unable to estimate distinctive coefficients. 

The following section will show how to prevent this issue in the right way. 

Avoiding the Dummy Variable Trap 

The dummy variable trap is easy to avoid once you understand why it occurs. The key idea is to remove redundancy created by encoding all categories of a feature. By using one fewer dummy variable than the number of categories, you eliminate perfect multicollinearity while preserving all the information needed by the model. The following steps show how to correctly encode categorical variables and safely interpret them in a linear regression setting.

Use k -1 Dummy Variables (Choose a Baseline Category)

The resolution to the dummy variable trap is easy. One less dummy variable than the categories. 

If a categorical feature has k different values, then form only k -1 dummy columns. The category that you omit turns out to be the category of reference, which is also the baseline. 

There is nothing lost by dropping one of the dummy columns. When the values of all dummies are 0 of a row, the current observation falls under the category of the baseline. 

There are three ice cream flavors in our case. That is to say that we are to have two dummy variables. We will eliminate one of the flavours and make it our baseline. 

Preventing the Dummy Variable Trap Using pandas

By convention, one category is dropped during encoding. In pandas, this is easily handled using drop_first=True. 

# Create dummy variables while dropping one category 
df_encoded = pd.get_dummies(df, columns=['Flavor'], drop_first=True) 
 
print(df_encoded)

Output:

   Sales   Flavor_Strawberry   Flavor_Vanilla
0   15          False              False
1   15          False              False
2   12          False               True
3   12          False               True
4   10           True              False
5   10           True              False

The encoded dataset now looks like this: 

• Sales 
• Flavor_Strawberry 
• Flavor_Vanilla 

Chocolate does not have its column. Chocolate has become the reference point. 

The rows are all easy to understand. When the Strawberry is 0 and Vanilla is 0, then the flavor should be Chocolate. The redundancy is now non-existent. The independent variables are the dummy ones. 

Then, it is how we escape the trap of the dummy variable. 

Interpreting the Encoded Data in a Linear Model 

Now let’s fit a simple linear regression model. We will predict Sales using the dummy variables. 

This example focuses only on the dummy variables for clarity. 

from sklearn.linear_model import LinearRegression 
 
# Features and target 
X = df_encoded[['Flavor_Strawberry', 'Flavor_Vanilla']] 
y = df_encoded['Sales'] 
 
# Fit the model 
model = LinearRegression(fit_intercept=True) 
model.fit(X, y) 
 
print("Intercept:", model.intercept_) 
print("Coefficients:", model.coef_) 

Output:

Intercept: 15.0
Coefficients: [-5.  -3.]

• ntercept (15) represents the average sales for the baseline category (Chocolate).
• Strawberry coefficient (-5) means Strawberry sells 5 units less than Chocolate.
• Vanilla coefficient (-3) means Vanilla sells 3 units less than Chocolate.

Each coefficient shows the effect of a category relative to the baseline, resulting in stable and interpretable outputs without multicollinearity. 

Best Practices and Takeaways 

Once you are aware of the trap of the dummy variable, it will be simple to avoid it. Follow one simple rule. When a categorical feature has k categories, then only k -1 dummy variables are used. 

The category that you omit turns out to be the reference category. All other categories are paralleled to it. This eliminates the ideal multicollinearity that would occur in case they are all included. 

This is mostly done right with the assistance of most modern tools. Pandas has the drop_first=True option in get_dummies, which will automatically drop one dummy column. The OneHotEncoder of scikit learn also has a drop parameter that can be utilised to do this safely. Most statistical packages, e.g., R or statsmodels, automatically omit one category in case a model has an intercept. 

Nevertheless, you are advised to be conscious of your tools. Whenever you generate dummy variables manually, be sure to drop one of the categories yourself. 

The elimination of one dummy is possible as it eliminates redundancy. It sets a baseline. The other coefficients have now displayed the difference between each category and that baseline. No information is lost. In the case of all the dummy values being 0, a given observation is in the reference category. 

The key takeaway is simple. Categorical data can be greatly incorporated into regression models using dummy variables. Never have more than one less dummy than the number of categories. This ensures that your model is stable, interpretable and does not have multicollinearity due to redundant variables. 

Conclusion 

Dummy variables are a necessary resource to deal with categorical data in machine learning models that need numbers. They permit representatives of categories to appear within correct or acceptable sense without any meaning of false order. Nonetheless, a dummy variable that uses an intercept and a dummy variable created upon each category results to the dummy variable trap. This will result in perfect multicollinearity, such that a variable will be redundant, and the model will not be able to determine unique coefficients. 

The solution is simple. When there are k categories of a feature, then only k -1 dummy variables should be used. The omitted category takes the form of the baseline. This eliminates duplication, maintains the model constant and results are readily interpreted.

If you want to learn all the basics of Machine Learning, checkout our Introduction to AI/ML FREE course!

Frequently Asked Questions