Part 18: Step by Step Guide to Master NLP – Topic Modelling using LDA (Probabilistic Approach)

This article was published as a part of the Data Science Blogathon

Introduction

This article is part of an ongoing blog series on Natural Language Processing (NLP).  In the previous part of this series, we completed our discussion on pLSA, which is a probabilistic framework for Topic Modelling. But we have seen some of the limitations of pLSA, so to resolve those limitations LDA comes into the picture.

So, In this article, we will discuss the probabilistic or Bayesian approach to understand the LDA. In the next article, we will also discuss the matrix factorization technique to understand the LDA and also see some more important concepts about Topic Modelling.

This is part-18 of the blog series on the Step by Step Guide to Natural Language Processing.

Table of Contents

1. What is Latent Dirichlet Allocation (LDA)?

2. LDA in a nutshell

3. Why do we need Dirichlet Distributions?

4. What are Dirichlet Distributions?

5. Probabilistic approach of LDA

6. Gibbs Sampling

Latent Dirichlet Allocation (LDA)

LDA stands for Latent Dirichlet Allocation. It is considered a Bayesian version of pLSA. In particular, it uses priors from Dirichlet distributions for both the document-topic and word-topic distributions, lending itself to better generalization. It is a particularly popular method for fitting a topic model.

The main assumption that LDA makes is that each document is generated by a statistical generative process i.e, each document is a mixture of topics, and each topic is a mixture of words. This algorithm exactly finding the weight of connections between documents and topics and between topics and words.

Image Source: Google Images

Since this technique treats each document as a mixture of topics, and each topic as a mixture of words so this allows documents to “overlap” each other in terms of content, rather than being divided into discrete groups, in a way that mirrors the typical use of natural language.

Image Source: Google Images

Let’s see what are the input and output to the LDA Algorithm?

Input: Document-term matrix, number of topics, and number of iterations.

Output: The top words in each topic. It is your job as a human to interpret this and see if the results make sense. If not, try altering the parameters such as terms in the document-term matrix, number of topics, number of iteration, etc. Stop when the topics make sense.

LDA in a nutshell

Let’s understand the meaning of each word in the title, as I think it contains everything that we need to know to understand how LDA works. LDA consists of the following three words:

• Latent
• Dirichlet
• Allocation

Now, understand the meaning of each word in a detailed manner:

Latent

Latent refers to everything that we don’t know a priori and are hidden in the data. Here, the themes or topics that the document consists of are unknown, but they are believed to be present as the text is generated based on those topics.

Dirichlet

It is a ‘distribution of distributions’ or you can understand it as a ‘family of distributions’.

But now a question comes to the mind or also we can say a doubt comes:

What does this mean as ‘distribution of distributions’?

Let’s understand this thing with the help of the following example:

Imagine you have a machine that produces dice and we have control over whether the machine will always produce a dice with equal weight to all sides, or will there be any bias for some sides.

So, this machine producing dice is considered as distribution since it produces dice of different types. Also, we know that the dice itself is a distribution since we can get multiple values when we roll a dice either fair or biased. This is the exact meaning of what it means to be a distribution of distributions and this is what Dirichlet is.

What does this represent in the context of Topic Modelling?

In the context of topic modelling, the Dirichlet is the distribution of topics in documents and the distribution of words in the topic.

Allocation

Once we have Dirichlet in our hands, we will allocate topics to the documents and words of the document to topics.

In short, the summary of all the above discussion is given below:

• ‘Latent’ represents that the model discovers the ‘yet-to-be-found’ or hidden topics from the documents.
• ‘Dirichlet’ represents LDA’s assumption that the distribution of topics in a document and the distribution of words in topics are both Dirichlet distributions.
• ‘Allocation’ represents the distribution of topics in the document.

That’s it. This is what LDA is in a nutshell.

Why do we need Dirichlet Distributions?

Dirichlet Distributions helps us to encode the intuition that documents are related to a few topics.

Importance-1:

In practical terms, this results in better disambiguation of words and a more precise assignment of documents to topics.

If we choose the random distribution, then the documents would be evenly distributed across all the topics. This implies that the documents have the same probability of being about one specific topic than to all topics at the same time.

But In real life, however, we know they are more sparsely distributed. Mostly, we can see most documents are tied to just one topic, while there’s still some probability to belong to multiple ones. And so happens between topics and words also.

So, Dirichlet distributions help us to model this type of behavior in a very natural way.

Importance-2: 

Let’s understand the importance of Dirichlet distribution with the help of the following example:

Imagine we have to compare the probability distributions of topic mixtures. Assume that the corpus on which we are focusing has documents from 3 very different subject areas. In these types of models, we want the type of distribution that gives very much weight to one specific topic and doesn’t give that much weight to the rest of other topics at all.

For Example, If we have 3 topics present in our corpus, then some specific probability distributions we would like to see are as follow:

• Mixture P: 90% topic A, 5% topic B, 5% topic C
• Mixture Q: 5% topic A, 90% topic B, 5% topic C
• Mixture R: 5% topic A, 5% topic B, 90% topic C

Now, if we draw a random probability distribution from this Dirichlet distribution that is parameterized by large weights on a single topic, we would likely get a distribution that strongly resembles either of the mixtures from P, Q, or R. And the possibility for us to sample a distribution that is 33% topic A, 33% topic B, and 33% topic C is very very less.

That’s essentially done with the help of Dirichlet distribution, a way of sampling probability distributions of a specific type.

Hope you understand the importance of Dirichlet distribution in LDA!

Test Your Previous Knowledge

1. In Linguistic Morphology which of the following process is used for reducing infected words to their root form?

• Stemming
• Rooting
• Text-profiling
• All of the above

2. Topic Modelling is ________ machine learning problem?

• Supervised
• Unsupervised
• Reinforcement
• Ensemble

3. Which of the following is not considered to be an NLP task?

• Image captioning
• Optical Character Recognition
• Machine Translation
• Image Classification

What are Dirichlet Distributions?

A Dirichlet distribution Dir(α) is a way to model a Probability Mass Function, which gives probabilities for discrete random variables.

Let’s understand this with the help of an example of rolling a die, which we also discuss in the above section of the article.

• It is a discrete random variable: The result is unpredictable, and the possible values can be 1, 2, 3, 4, 5, or 6.
• If we have a fair dice, then a PMF would give the probabilities such as [0.16, 0.16, 0.16, 0.16, 0.16, 0.16]
• If we have biased dice, then a PMF could return the probabilities: such as [0.25, 0.15, 0.15, 0.15, 0.15, 0.15], i.e, obtaining a one is higher than the other sides of the dice.

In the example with documents, topics, and words, we’ll have two PMFs:

ϴtd: the probability of topic k occurring in document d

Фwt: the probability of word w occurring in topic k

The α in Dir(α) is known as the concentration parameter, and rules the trend of the distribution to be:

• Uniform (α =1),
• Concentrated (α > 1),
• Sparse (α < 1)

By using a concentration parameter α < 1 the above probabilities will be closer to the real world. In other words, they follow Dirichlet distributions. Therefore, 

ϴtd ~ Dir( α) and  Фwt ~ Dir(β), 

where α and β rule each distribution and both have values < 1.

Self Learning: If you want to know more about or in-depth about Dirichlet distributions refer to the following links:

Link-1,  Link-2

Probabilistic Approach of LDA

In our discussion on LDA, we see that LDA says is that each word in each document comes from a topic and the topic is selected from a per-document distribution over topics. So we have two matrices- one related to topic and document and the other related to word and topic.

ϴtd = P(t|d) which represents the probability distribution of topics in documents
Фwt = P(w|t) which represents the probability distribution of words in topics

And, the probability of a word given document i.e. P(w|d) is equal to:

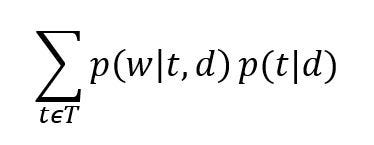
where 

T represents the total number of topics.

W represents the total number of words in our dictionary for all the documents.

If we assume conditional independence, we can say that

P(w|t,d) = P(w|t)

And hence the expression of P(w|d) reduces to:

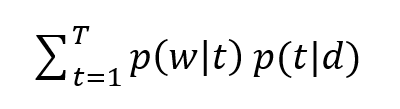
i.e, it is the dot product of ϴtd and Фwt for each topic t.

Now, let’ see the step by step procedure of the probabilistic approach for LDA is shown below:

Step-1

Go through each of the documents in a corpus and randomly assign each word in the document to one of K topics (K is chosen beforehand or given by the user).

Step-2

With the help of random assignment, we got the topic representations for all the documents and word distributions of all the topics, but these are not very good ones.

Step-3

So, to improve upon them

For each document d, we go through each word w and compute the following:

• p(topic t | document d): represents the proportion of words present in document d that are assigned to topic t of the corpus.
• p(word w | topic t): represents the proportion of assignments to topic t, over all documents d, that comes from word w.

Step-4

Reassign word w a new topic t’, where we choose topic t’ with probability p(topic t’ | document d)* p(word w | topic t’)

This generative model predicts the probability that topic t’ generate word w.

Step-5

Repeating step-4 a large number of times, up to we reach a steady-state and at that state the topic assignments are pretty good. And finally, we use these assignments to determine the topic mixtures of each document.

Step-6

After completing a certain number of iterations, we achieved a steady state where the document topic and topic term distributions are fairly good. And this becomes the convergence point of LDA.

Problem with above steps

In the above process, if our guess of the weights is wrong, then the actual data that we observe will be very unlikely under our assumed weights and data generating process. Therefore, to resolve that issue we are trying to maximize the likelihood of our data given these two matrices.

To identify the correct weights, we will use an algorithm known as Gibbs sampling. Let’s now understand Gibbs sampling and its working in LDA in the next section.

Test Your Knowledge

1. While extracting features or terms from the document, the number of topics is recommended to be?

• Higher number
• Lower number
• Between 0 and 1
• Between -1 and 1

2. Which of the following statements are true with respect to LDA?

• Documents exhibit multiple topics
• LDA is a probabilistic model with a corresponding generative process
• A topic is a distribution over a fixed vocabulary
• All of these

Gibbs Sampling

It is an algorithm that can be used for successively sampling conditional distributions of variables, whose distribution over states converges to the true distribution in the long run.

Here, In this blog post, we will not going to discuss the maths behind Gibbs Sampling but will try to give an intuition on how Gibbs Sampling work to identify topics in the documents.

As we discussed earlier, we will assume that we know ϴ and Ф matrices. Now we will slowly change these matrices and get to an answer that maximizes the likelihood of the data that we have. This process is done on a word-by-word basis by changing the topic assignment of one word.

Assumption: We will assume that we don’t know the topic assignment of the given word but we know the assignment of all other words in the text and we will try to find the topics that will be assigned to this word.

In mathematical terms, we are trying to find the conditional probability distribution of a single word’s topic assignment conditioned on the rest of the topic assignments.

Ignoring all the mathematical calculations, we will get a conditional probability equation that looks like this for a single word w in document d that belongs to topic k:

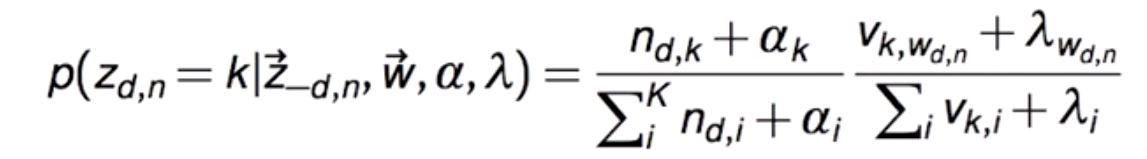
where:

n_(d,k): represents how many time a document d use topic k

v_(k,w): represents how many times a topic k uses the given word

α_k: Dirichlet parameter for the document to topic distribution

λ_w: Dirichlet parameter for the topic to word distribution

If you observe carefully in the above expression, we divide that complete expression into two parts. Now, let’s see the importance of each part.

The first part tells us how much each topic is present in a document and the second part tells how much each topic likes a word.

Here we have to note that for each word, we will get a vector of probabilities that will explain how likely this word belongs to each of the topics. In the above equation, we also observe that the Dirichlet parameters can also act as smoothing parameters when the terms n(d,k) or v(k,w) goes to zero which means that there will still be some possibility that the word will choose a topic going forward.

After including Gibbs sampling in our probabilistic approach of LDA, the pictorial representation of all the steps is as follows:

                                 Image Source: Google Images

Finally, as a concluding step or just outline the intuition behind the training process with Gibbs Sampling:

• Randomly assign a topic to each word in the initial documents of the corpus.
• Reassign the topic of each word such that each document contains the minimum possible topics.
• Also, reassign the word of each topic such that each word is assigned the minimum possible topics.

For more about this topic, please have a look here.

Homework Problems

Question-1: Find out some of the differences between LSA and LDA Topic modelling techniques.

Question-2: Why LDA is known as the Bayesian Version of pLSA?

Question-3: Which limitations of pLSA are overcome by the LDA?

If you want to learn more about the LDA, then read the following paper:

                    Read the Paper

Other Blog Posts by Me

You can also check my previous blog posts.

Previous Data Science Blog posts.

LinkedIn

Here is my Linkedin profile in case you want to connect with me. I’ll be happy to be connected with you.

Email

For any queries, you can mail me on Gmail.

End Notes

Thanks for reading!

I hope that you have enjoyed the article. If you like it, share it with your friends also. Something not mentioned or want to share your thoughts? Feel free to comment below And I’ll get back to you. 😉

Chirag Goyal

I am a B.Tech. student (Computer Science major) currently in the pre-final year of my undergrad. My interest lies in the field of Data Science and Machine Learning. I have been pursuing this interest and am eager to work more in these directions. I feel proud to share that I am one of the best students in my class who has a desire to learn many new things in my field.