Introduction
Large language models (LLMs) have dramatically reshaped computational mathematics. These advanced AI systems, designed to process and mimic human-like text, are now pushing boundaries in mathematical fields. Their ability to understand and manipulate complex concepts has made them invaluable in research and development. Among these innovations stands Paramanu-Ganita, a creation of Gyan AI Research. This model, though only 208 million parameters strong, outshines many of its larger counterparts. It’s specifically built to excel in mathematical reasoning, demonstrating that smaller models can indeed perform exceptionally well in specialized domains. In this article, we will explore the development and capabilities of the Paramanu-Ganita AI model.

Table of Contents
The Rise of Smaller Scale Models
While large-scale LLMs have spearheaded numerous AI breakthroughs, they come with significant challenges. Their vast size demands extensive computational power and energy, making them expensive and less accessible. This has prompted a search for more viable alternatives.
Smaller, domain-specific models like Paramanu-Ganita prove advantageous. By focusing on specific areas, such as mathematics, these models achieve higher efficiency and effectiveness. Paramanu-Ganita, for instance, requires fewer resources and yet operates faster than larger models. This makes it ideal for environments with limited resources. Its specialization in mathematics allows for refined performance, often surpassing generalist models in related tasks.
This shift towards smaller, specialized models is likely to influence the future direction of AI, particularly in technical and scientific fields where depth of knowledge is crucial.
Development of Paramanu-Ganita
Paramanu-Ganita was developed with a clear focus: to create a powerful, yet smaller-scale language model that excels in mathematical reasoning. This approach counters the trend of building ever-larger models. It instead focuses on optimizing for specific domains to achieve high performance with less computational demand.
Training and Development Process
The training of Paramanu-Ganita involved a curated mathematical corpus, selected to enhance its problem-solving capabilities within the mathematical domain. It was developed using an Auto-Regressive (AR) decoder and trained from scratch. Impressively, it managed to reach its objectives with just 146 hours of training on an Nvidia A100 GPU. This is just a fraction of the time larger models require.

Unique Features and Technical Specifications
Paramanu-Ganita stands out with its 208 million parameters, a significantly smaller number compared to the billions often found in large LLMs. This model supports a large context size of 4096, allowing it to handle complex mathematical computations effectively. Despite its compact size, it maintains high efficiency and speed, capable of running on lower-spec hardware without performance loss.
Performance Analysis
Paramanu-Ganita’s design greatly enhances its ability to perform complex mathematical reasoning. Its success in specific benchmarks like GSM8k highlights its ability to handle complex mathematical problems efficiently, setting a new standard for how language models can contribute to computational mathematics.
Comparison with Other LLMs like LLaMa, Falcon, and PaLM
Paramanu-Ganita has been directly compared with larger LLMs such as LLaMa, Falcon, and PaLM. It shows superior performance, particularly in mathematical benchmarks, where it outperforms these models by significant margins. For example, despite its smaller size, it outperforms Falcon 7B by 32.6% points and PaLM 8B by 35.3% points in mathematical reasoning.
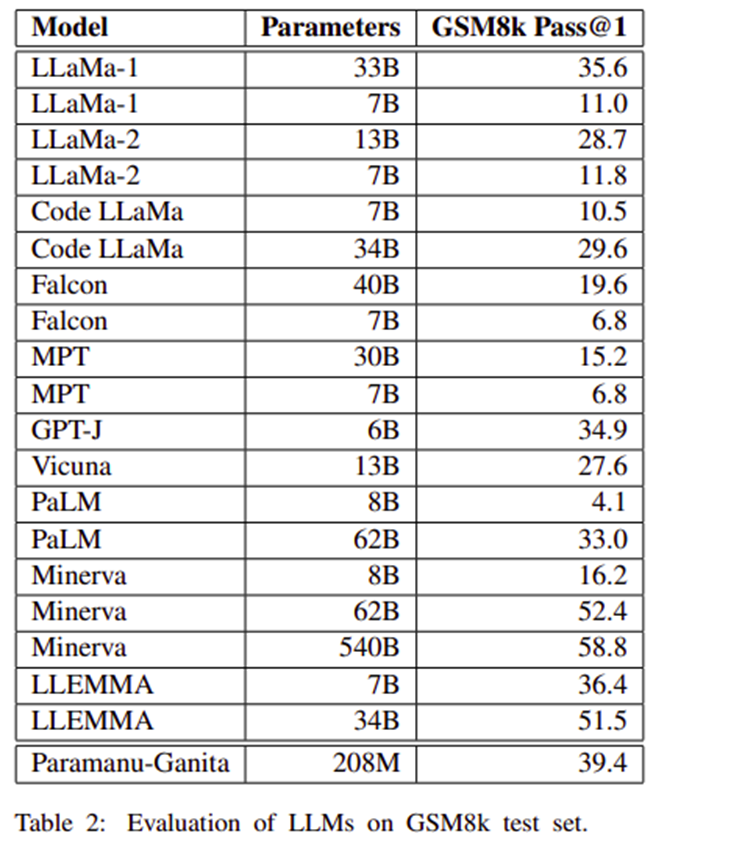
Detailed Performance Metrics on GSM8k Benchmarks
On the GSM8k benchmark, which evaluates the mathematical reasoning capabilities of language models, Paramanu-Ganita achieved remarkable results. It scored higher than many larger models, demonstrating a Pass@1 accuracy that surpasses LLaMa-1 7B and Falcon 7B by over 28% and 32% points, respectively. This impressive performance underlines its efficiency and specialized capability in handling mathematical tasks, confirming the success of its focused and efficient design philosophy.
Implications and Innovations
One of the key innovations of Paramanu-Ganita is its cost-effectiveness. The model requires significantly less computational power and training time compared to larger models, making it more accessible and easier to deploy in various settings. This efficiency does not compromise its performance, making it a practical choice for many organizations.
The characteristics of Paramanu-Ganita make it well-suited for educational purposes, where it can assist in teaching complex mathematical concepts. In professional environments, its capabilities can be leveraged for research in theoretical mathematics, engineering, economics, and data science, providing high-level computational support.
Future Directions
The development team behind Paramanu-Ganita is actively working on an extensive study to train multiple pre-trained mathematical language models from scratch. They aim to investigate whether various combinations of resources—such as mathematical books, web-crawled content, ArXiv math papers, and source code from relevant programming languages—enhance the reasoning capabilities of these models.
Additionally, the team plans to incorporate mathematical question-and-answer pairs from popular forums like StackExchange and Reddit into the training process. This effort is designed to assess the full potential of these models and their ability to excel on the GSM8K benchmark, a popular math benchmark.
By exploring these diverse datasets and model sizes, the team hopes to further improve the reasoning ability of Paramanu-Ganita and potentially surpass the performance of state-of-the-art LLMs, despite Paramanu-Ganita’s relatively smaller size of 208 million parameters.
Paramanu-Ganita’s success opens the door to broader impacts in AI, particularly in how smaller, specialized models could be designed for other domains. Its achievements encourage further exploration into how such models can be utilized in computational mathematics. Ongoing research in this domain shows potential in handling algorithmic complexity, optimization problems, and beyond. Similar models thus hold the power to reshape the landscape of AI-driven research and application.
Conclusion
Paramanu-Ganita marks a significant step forward in AI-driven mathematical problem-solving. This model challenges the need for larger language models by proving that smaller, domain-specific solutions can be highly effective. With outstanding performance on benchmarks like GSM8k and a design that emphasizes cost-efficiency and reduced resource needs, Paramanu-Ganita exemplifies the potential of specialized models to revolutionize technical fields. As it evolves, it promises to broaden the impact of AI, introducing more accessible and impactful computational tools across various sectors, and setting new standards for AI applications in computational mathematics and beyond.







