Simple Framework to crack a Kaggle problem statement

It is an exciting times at Kaggle: 5 simultaneous competitions with significant prize value – Santa is definitely out there looking for good data scientists across the globe! I have put in at least one shot in all the 5 competitions. Every attempt enlightens me with new tricks to make a better prediction. Even though I started competing on this forum just 4 months back, I feel confident of getting a decent score in first attempt. In this article, I will share a few tips and tricks to approach these competitions.

Big Question : What is Kaggle?

Here is how Wiki defines Kaggle : “Kaggle is a platform for predictive modelling and analytics competitions on which companies and researchers post their data and statisticians and data miners from all over the world compete to produce the best models.”

Kaggle competitions are all about making the best prediction – by hook or by crook. This process can involve significant labor such as the Santa problem or might involve some common Kaggle tricks such as Data Science London Problem.

Some Hacks to Keep in mind before competing:

Competing with the best data scientists can be challenging. Especially so, if some of them have been doing so for years. I know a few people who have well automated scripts to perform most of the data exploration! These people are out deciding on best algorithms when rest of the world is still figuring out the nuances of the data.

Here are a few things you need to keep in mind before starting a problem on Kaggle :

1. Like all good things in life, winning a Kaggle competition is all about hard work. Get ready to devote long hours wondering on the same problem for days/weeks/months.
2. Team up with a good team mate for competing in initial competitions. Good team mate is some one with similar bent of mind and thought process, but might have complementary skills on tool / domain / work experience.
3. Be ready to do a lot of feature engineering – that is what differentiates the best from the rest.
4. Do a preliminary research on the domain and the problem. There might be good research papers with non-conventional effective solutions available on the internet.
5. Make simple initial solutions and submit them to get a sense on how much gap you need to cover
6. Always be open to start from scratch
7. Experiment with different algorithms and be prepared to prepare ensembles.

The list is not exhaustive, but covers a significant portion. Now let’s look at a simple framework to approach a Kaggle problem. Participants are challenged at each step of this framework by Kaggle.

Framework to approach a Kaggle Problem

Next, we will take you through a step by step process of taking a simple shot on a Kaggle statement. The process generally involve following pieces :

1. Importing the training / test population : Kaggle challenges you to import the training / test dataset. In general, this is not very straight forward. For example in following problems, training data needs to messaged well before we start working on the model.

Here are two problem statements where you need to extract data from multiple excel files :

a. Driver Telematic Analysis

b. BCI Challenge @ NER 2015

2. Sampling the population : In general the population size is huge and might not be the best idea to train using the entire population. For example, “Sentiment Analysis fro Movie Review” with an enormous number of phrases might be a bad idea to build an initial dictionary. Choosing this sample can be done randomly or in a stratified way.

3. Choosing the right attributes : This is the most critical step which distinguishes different submissions on Kaggle. In general we use Principle component analysis, factor analysis, Information Value, Weight of Evidence to do this part. But there is no set procedure to do this.

4. Compare different ensemble / simple models : Once we have the input and the target variables, we start building different models. The choice of model depends on the evaluation metrics, type of input / target variable, distribution of population on target values etc.

In this article we will start with the first step leveraging the BCI challenge. We will start with the problem statement and then define the scope of this article. After reading this article, I believe you can start competing on Kaggle and start your journey to discover the new era of Analytics & Machine Learning.

Kaggle Problem

Twenty-six healthy subjects took part in this study (13 male, mean age = 28.8±5.4 (SD), range 20-37). All subjects reported normal or corrected-to-normal vision and had no previous experience with the P300-Speller paradigm or any other BCI application. Subject’s brain activity was recorded with 56 passive Ag/AgCl EEG sensors (VSM-CTF compatible system) whose placement followed the extended 10-20 system. Their signals were sampled at 600 Hz and were all referenced to the nose. The ground electrode was placed on the shoulder and impedences were kept below 10 kΩ.

The subjects had to go through five copy spelling sessions. Each session consisted of twelve 5-letter words, except the fifth which consisted of twenty 5-letter words. You need to build Error Potential detection algorithm, capable of detecting the erroneous feedback online.

Your Task

You have two folders called Test and Train. Each of these folders contains a number of files (These files can be downloaded from here). Each of these files contain data entry on the subject for every 5 mili seconds. At a few points we observe FeedBack Event, which is denoted by flag 1. We need to pull 261 observations starting from this response for 1 variable :

1. Cz

Finally you need to put these information in the same row as that of subject – feedback number combination. For instance, if we are looking for subject – 02, 1 st response : we need to look for first 261 observations on the 1 attribute from the first feedback event.

Solution

First thing first, let’s import all the required libraries and initialize the subjects which are part of training or test,

from __future__ import division
import numpy as np
import pandas as pd

train_subs = ['02','06','07','11','12','13','14','16','17','18','20','21','22','23','24','26']

test_subs = ['01','03','04','05','08','09','10','15','19','25']

Once we have all the libraries defined and subject list created, the second step is to create dataframe which can hold our extracted data:

train = pd.DataFrame(columns=[‘subject’,’session’,’feedback_num’,’start_pos’] + [‘Cz’ + s for s in map(str,range(261))] ,index=range(5440))

After creating a dataframe, we need to open individual file and extract relevant data. Then we need to store this extracted data in the already created dataframe.

[stextbox id="grey"]
 counter = 0
 data = {}
 for i in train_subs:
    for j in range(1,6):
        temp = pd.read_csv('train/Data_S' + i + '_Sess0'  + str(j) + '.csv')
        fb = temp.query('FeedBackEvent == 1',engine='python')['FeedBackEvent']
        counter2 = 0
        for k in fb.index:
             temp2 = temp.loc[int(k):int(k)+260,'Cz']
             temp2.index = ['Cz' + s for s in map(str,range(261))]
             train.loc[counter,['Cz' + s for s in map(str,range(261))]] = temp2
             train.loc[counter,'session'] = j
             train.loc[counter, 'subject'] = i
             train.loc[counter, 'feedback_num'] = counter2
             train.loc[counter, 'start_pos'] = k
             counter +=1
             counter2 +=1
    print 'subject ', i
train.to_csv('train_6var.csv',ignore_index=True)[/stextbox]

Once we have all the information in a single place, we can now start doing some initial analysis. For instance, lets find the first two principle components and plot the target variable to see how infused are the responders and non-responders. You can use the following code to do this analysis :

pca2 = PCA(n_components=2, whiten=True)

y = pd.read_csv(‘TrainLabels.csv’).values[:,1].ravel()

pca2.fit(np.r_[train, test])
X_pca = pca2.transform(train)
i0 = np.argwhere(y == 0)[:, 0] i1 = np.argwhere(y == 1)[:, 0] X0 = X_pca[i0, :] X1 = X_pca[i1, :] plt.plot(X0[:, 0], X0[:, 1], ‘ro’)
plt.plot(X1[:, 0], X1[:, 1], ‘b*’)

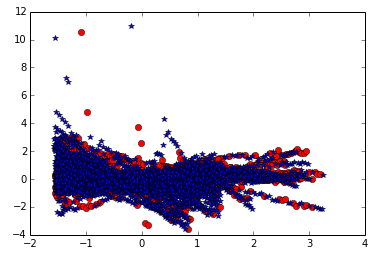
As you can see from the above image that the responders and non responders are well segregated from each other using the currently available attributes. Hence, with only a single variable you can implement machine learning tools to bring out decent predictions.

End Notes

Once you have extracted the relevant data using Python, you can start implementing various initial analysis and prediction by machine learning algorithms. In next few articles we will take you through the entire process to build a simple solution and will be closing at a decent place on leadership board in Kaggle. We will also take up a few more examples of data extraction which includes extraction of data from picture files or extracting data from websites.

Did you find the article useful? Share with us if you have done similar pieces on tools like R and SAS. Do let us know your thoughts about this article in the box below.

If you like what you just read & want to continue your analytics learning, subscribe to our emails, follow us on twitter or like our facebook page.

Tavish Srivastava

Tavish Srivastava, co-founder and Chief Strategy Officer of Analytics Vidhya, is an IIT Madras graduate and a passionate data-science professional with 8+ years of diverse experience in markets including the US, India and Singapore, domains including Digital Acquisitions, Customer Servicing and Customer Management, and industry including Retail Banking, Credit Cards and Insurance. He is fascinated by the idea of artificial intelligence inspired by human intelligence and enjoys every discussion, theory or even movie related to this idea.