Why You Shouldn’t Just Delete Outliers

This article was published as a part of the Data Science Blogathon.

Introduction

Outliers are a very important and crucial aspect of Data Analysis. While doing data preprocessing for a Data Science project, we always think about the extreme values present in the dataset, i.e, should we keep those values for our analysis or we have to just delete them from our dataset.

Let’s highlight the difference between natural and non-natural outliers?

The non-natural outliers are those which are caused by measurement errors, wrong data collection, or wrong data entry whereas natural outliers could be the use case of fraudulent transactions in banking data, etc.

No matter how alert you are during the data collection, every Data Analyst has felt the frustration of finding the outliers. Outliers are one of those problems which we come across almost every time while doing machine learning modeling.

Now, a question comes to mind: ” Are Outliers and Noise the same”?

The answer to this question is “No” since outliers are different from the noise data.

• Noise is considered as a random error or the variance in a measured variable.

• The process of noise removal should be done before outlier detection.

Table of Contents

👉 What are Outliers?

👉 When are outliers dangerous?

👉 Which statistics are affected by the outliers?

👉 When to drop or keep outliers?

What are Outliers?

In terms of statistics, Outliers can be defined as,

“An Outlier is that observation which is significantly different from all other observations.”

From this definition, we can conclude that an outlier is something that is an odd-one-out or the one that is different from the crowd. Some statisticians formally define outliers as ‘Observations having a different underlying behavior than the rest of the observations’.

Alternatively, outliers are those observations that are significantly different from other observations.

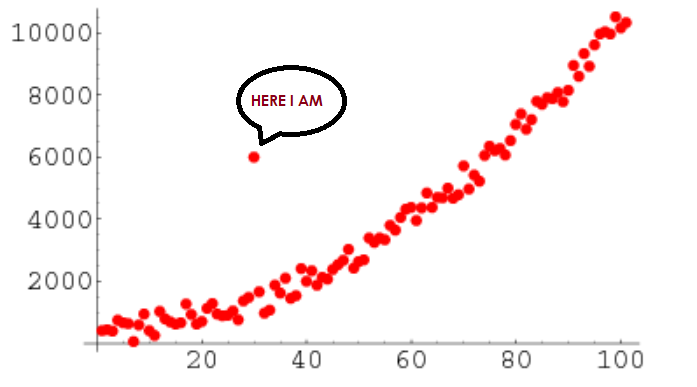
Fig. Image showing an outlier

Image Source: link

An analogy of Outliers in Real-life Examples,

Example-1: In a class, we have 100 students and one student who always scores marks on the higher side concerning other students and its score is not much dependent on the Difficulty level of the exam. So, here we consider that guy as an outlier.

Example-2:  let’s have to find the average salary of a group of people and accidentally Bill Gates or Elon Musk-like people entered the group. So, think now about the average salary of new groups of people. Here average salary is not a true representation due to outliers.

When are outliers dangerous?

Outliers are not always dangerous for our problem statement. In fact, outliers sometimes can be helpful indicators.

They represent errors in the measurement, bad data collection(not careful while data collection), or simply show those variables that are not considered while collecting the data. Many data analysts are directly tempted to delete outliers. However, this is sometimes the wrong choice for our predictive analysis. One cannot recognize outliers while collecting the data for the problem statement; you won’t know what data points are outliers until you begin analyzing the data. Since some of the statistical tests are sensitive to the outliers and therefore, the ability to detect them and treat them accordingly is an important part of data analytics.

Let’s consider the following three different scenarios,

Scenario-1: Let’s we have a data of Age for population and the age of a people in that data is 356, and we know that the age value 356 is not possible, so here this data point considered as an outlier and we not know what value we have to replace to this value. So, we have to remove the data point completely from our dataset.

Fig. Showing point for Age=356

Image Source: link

Scenario-2: Let’s have a use case of credit card fraud detection, outlier analysis becomes important because here, the exception rather than the rule may be of interest to the analyst.

Scenario-3: Let’s have a regression problem, whereas hours of study are the independent variable and marks are a dependent variable. We have some outliers present, so they attract the line of regression to our side. To resolve this, we can create an IQ column then the outlier behavior may be justified from the IQ column.

Fig. Effect of outliers on the regression line

Image Source: link

From these three scenarios, we conclude that the role of outliers is different for different problem statements. So, the main problem is what we have to do with outliers, but finding the outliers in our dataset is not a very difficult task.

Which statistics are affected by the outliers?

Let’s discuss one by one for each statistic,

👉 Mean: It is the only measure of central tendency that is always affected by an outlier since it is calculated as the sum of the observed values and then divide by the total number of observations. Since in the expression of mean, the total sum is included, and due to outliers, there are some abnormal values i.e. Outliers will affect this sum.

For Example, the Let’s outlier is having a bigger positive value than the other values that will make the sum large enough so that the mean will also be slightly larger while if the outlier has a very small value, then the mean will also become a bit smaller. Hence the presence of outliers in our dataset can largely affect the mean.

👉 Standard deviation (SD): It is calculated with the help of every observation in the data set. It is a sensitive measure because it will be influenced by outliers since standard deviation is calculated by taking the difference of sample case from the mean, outliers will affect Standard deviation.

👉 Median: The median is defined as the middle value in a particular distribution. It is the data point at which half of the observations are above, and half of the observations are below wrt that point. It is not affected by outliers, therefore the median is preferred as a measure of central tendency when a distribution has extreme observations.

👉 Inter-Quartile Range (IQR): The IQR is the difference between the 75th and 25th percentile. The IQR is more resistant to outliers. The IQR by definition only covers the middle 50% of the data, so outliers are well outside this range and the presence of a small number of outliers is not likely to change this significantly. If you add an outlier, the IQR will change to another set of data points that are probably not that dissimilar to the previous ones (in most datasets), hence it is “resistant” to change. This is especially the case of a large dataset.

Now if you add some crazy extreme data point at the end, the 75th and 25th percentile doesn’t change much, because extreme outliers or no, 75% of the data still lies below roughly the same amount.

👉Range: Most affected by the outliers since it is the difference b/w the max and min value present in the dataset.

When to drop or keep outliers?

I believe that the dropping outlier is always a harsh step and should be taken only in extreme conditions when we’re very sure that the outlier is due to a measurement error, which we generally do not know while doing analysis.

Sometimes outliers indicate a mistake in data collection. Other times, though, they can influence a data set, so it’s important to keep them to better understand the dataset in the big picture.

Below are some examples that give you a clear idea about when you should and shouldn’t drop outliers.

Drop an outlier if:

👉 You know that it’s completely wrong

For example, if you have a really good sense of how range our data should fall in, like people’s ages, which we discussed above in scenario-1, you can safely drop values outside of that range.

👉 You have a lot of data in hand

When you have a lot of data in your hands, then your sample won’t be hurt by dropping a questionable outlier.

👉 You have an option to going back

You can go back and recollect and verify the questionable observations.

Don’t drop an outlier if:

👉 Your results are critical

 When your results are critical, then even minor changes will matter a lot.

For example, You can feel better about dropping outliers of the dataset in which there are people’s favorite TV shows, but not about the temperatures at which airplane seals fail.

👉 There are a lot of outliers

By definition, Outliers are rare.

For example, Let’s 25% of your data be outliers, then it means that something is interesting going on with your data that you need to look further into. You can relate this with scenario-2 which we discussed in the above section.

End Notes

Thanks for reading!

If you liked this and want to know more, go visit my other articles on Data Science and Machine Learning by clicking on the Link

Please feel free to contact me on Linkedin, Email.

Something not mentioned or want to share your thoughts? Feel free to comment below And I’ll get back to you.

About the author

Chirag Goyal

Currently, I am pursuing my Bachelor of Technology (B.Tech) in Computer Science and Engineering from the Indian Institute of Technology Jodhpur(IITJ). I am very enthusiastic about Machine learning, Deep Learning, and Artificial Intelligence.

The media shown in this article are not owned by Analytics Vidhya and is used at the Author’s discretion. 

Chirag Goyal

I am a B.Tech. student (Computer Science major) currently in the pre-final year of my undergrad. My interest lies in the field of Data Science and Machine Learning. I have been pursuing this interest and am eager to work more in these directions. I feel proud to share that I am one of the best students in my class who has a desire to learn many new things in my field.