Interview Prep
Career
GenAI
Prompt Engg
ChatGPT
LLM
Langchain
RAG
AI Agents
Machine Learning
Deep Learning
GenAI Tools
LLMOps
Python
NLP
SQL
AIML Projects

Reading list

Machine Learning Basics for a Newbie
6 Steps of Machine learning Lifecycle Introduction to Predictive Modeling
Introduction to Exploratory Data Analysis & Data Insights Descriptive Statistics Inferential Statistics How to Understand Population Distributions?
Reading Data Files into Python Different Variable Datatypes
Probability for Data Science Basic Concepts of Probability Axioms of Probability Conditional Probability
Central Tendencies for Continuous Variables Spread of Data KDE plots for Continuous Variable Overview of Distribution for Continuous variables Normal Distribution Skewed Distribution Skeweness and Kurtosis Distribution for Continuous Variable
Central Tendencies for Categorical Variables Understanding Discrete Distributions Performing EDA on Categorical Variables
Dealing with Missing Values Understanding Outliers Identifying Outliers in Data Outlier Detection in Python Outliers Detection Using IQR, Z-score, LOF and DBSCAN
Sample and Population Central Limit Theorem Confidence Interval and Margin of Error
Bivariate Analysis Introduction
Covariance Pearson Correlation Spearman's Correlation & Kendall's Tau Correlation versus Causation Tabular and Graphical methods for Bivariate Analysis Performing Bivariate Analysis on Continuous-Continuous Variables
Tabular and Graphical methods for Continuous-Categorical Variables Introduction to Hypothesis Testing P-value Two sample Z-test T-test T-test vs Z-test Performing Bivariate Analysis on Continuous-Catagorical variables
Chi-Squares Test Bivariate Analysis on Categorical Categorical Variables
Multivariate Analysis A Comprehensive Guide to Data Exploration The Data Science behind IPL
Supervised Learning vs Unsupervised Learning Reinforcement Learning Generative and Descriminative Models Parametric and Non Parametric model
Machine Learning Pipeline Preparing Dataset Build a Benchmark Model: Regression Build a Benchmark Model: Classification
Evaluation Metrics for Machine Learning Everyone should know Confusion Matrix Accuracy Precision and Recall AUC-ROC Log Loss R2 and Adjusted R2
Dealing with Missing Values Replacing Missing Values Imputing Missing Values in Data Working with Categorical Variables Working with Outliers Preprocessing Data for Model Building
Understanding Cost Function Understanding Gradient Descent Math Behind Gradient Descent Assumptions of Linear Regression Implement Linear Regression from Scratch Train Linear Regression in Python Implementing Linear Regression in R Diagnosing Residual Plots in Linear Regression Models Generalized Linear Models Introduction to Logistic Regression Odds Ratio Implementing Logistic Regression from Scratch Introduction to Scikit-learn in Python Train Logistic Regression in python Multiclass using Logistic Regression How to use Multinomial and Ordinal Logistic Regression in R ? Challenges with Linear Regression Introduction to Regularisation Implementing Regularisation Ridge Regression Lasso Regression
Introduction to K Nearest Neighbours Determining the Right Value of K in KNN Implement KNN from Scratch Implement KNN in Python
Bias Variance Tradeoff Introduction to Overfitting and Underfitting Visualizing Overfitting and Underfitting Selecting the Right Model What is Validation? Hold-Out Validation Understanding K Fold Cross Validation
Introduction to Feature Selection Feature Selection Algorithms Missing Value Ratio Low Variance Filter High Correlation Filter Backward Feature Elimination Forward Feature Selection Implement Feature Selection in Python Implement Feature Selection in R
Introduction to Decision Tree Purity in Decision Tree Terminologies Related to Decision Tree How to Select Best Split Point in Decision Tree? Chi-Squares Information Gain Reduction in Variance Optimizing Performance of Decision Tree Train Decision Tree using Scikit Learn Pruning of Decision Trees
Introduction to Feature Engineering Feature Transformation Feature Scaling Feature Engineering Frequency Encoding Automated Feature Engineering: Feature Tools
Introduction to Naive Bayes Conditional Probability and Bayes Theorem Introduction to Bayesian Adjustment Rating: The Incredible Concept Behind Online Ratings! Working of Naive Bayes Math behind Naive Bayes Types of Naive Bayes Implementation of Naive Bayes
Understanding how to solve Multiclass and Multilabled Classification Problem Evaluation Metrics: Multi Class Classification
Introduction to Ensemble Techniques Basic Ensemble Techniques Implementing Basic Ensemble Techniques Finding Optimal Weights of Ensemble Learner using Neural Network Why Ensemble Models Work well?
Introduction to Stacking Implementing Stacking Variants of Stacking Implementing Variants of Stacking Introduction to Blending Bootstrap Sampling Introduction to Random Sampling Hyper-parameters of Random Forest Implementing Random Forest Out-of-Bag (OOB) Score in the Random Forest IPL Team Win Prediction Project Using Machine Learning Introduction to Boosting Gradient Boosting Algorithm Math behind GBM Implementing GBM in python Regularized Greedy Forests Extreme Gradient Boosting Implementing XGBM in python Tuning Hyperparameters of XGBoost in Python Implement XGBM in R/H2O Adaptive Boosting Implementing Adaptive Boosing LightGBM Implementing LightGBM in Python Catboost Implementing Catboost in Python
Different Hyperparameter Tuning methods Implementing Different Hyperparameter Tuning methods GridsearchCV RandomizedsearchCV Bayesian Optimization for Hyperparameter Tuning Hyperopt
Understanding SVM Algorithm SVM Kernels In-depth Intuition and Practical Implementation SVM Kernel Tricks Kernels and Hyperparameters in SVM Implementing SVM from Scratch in Python and R
Introduction to Principal Component Analysis Steps to Perform Principal Compound Analysis Computation of Covariance Matrix Finding Eigenvectors and Eigenvalues Implementing PCA in python Visualizing PCA A Brief Introduction to Linear Discriminant Analysis Introduction to Factor Analysis
Introduction to Clustering Applications of Clustering Evaluation Metrics for Clustering Understanding K-Means Implementation of K-Means in Python Implementation of K-Means in R Choosing Right Value for K Profiling Market Segments using K-Means Clustering Hierarchical Clustering Implementation of Hierarchial Clustering DBSCAN Defining Similarity between clusters Build Better and Accurate Clusters with Gaussian Mixture Models
Understand Basics of Recommendation Engine with Case Study
8 Ways to Improve Accuracy of Machine Learning Models
Introduction to Dask Working with CuML
Introduction to Machine Learning Interpretability Framework and Interpretable Models model Agnostic Methods for Interpretability Implementing Interpretable Model Understanding SHAP Out-of-Core ML Introduction to Interpretable Machine Learning Models Model Agnostic Methods for Interpretability Game Theory & Shapley Values
Introduction to Machine Learning Interpretability Framework and Interpretable Models model Agnostic Methods for Interpretability Implementing Interpretable Model Understanding SHAP Out-of-Core ML Introduction to Interpretable Machine Learning Models Model Agnostic Methods for Interpretability Game Theory & Shapley Values
Introduction to AutoML Implementation of MLBox Introduction to PyCaret TPOT Auto-Sklearn EvalML
Pickle and Joblib Introduction to Model Deployment
Deploying Machine Learning Model using Streamlit Deploying ML Models in Docker Deploy Using Streamlit Deploy on Heroku Deploy Using Netlify Introduction to Amazon Sagemaker Setting up Amazon SageMaker Using SageMaker Endpoint to Generate Inference Deploy on Microsoft Azure Cloud Introduction to Flask for Model Deploying ML model using Flask
Model Deployment in Android Model Deployment in Iphone

Extracting right variables for your Regression model

Tavish Srivastava
Tavish Srivastava Last Updated : 25 Jun, 2020
4 min read

Getting the right variables in your model and cleaning them can make or break your model.

The precision of the model depends on the breadth (diversity) and depth (spread of data and correct transformations) of variables. This article will take you through some of the techniques used in the industry to create or transform variables. We will also cover the techniques used in the industry to select the right set of variables out of an exhaustive list created in our next article on the subject.

variables2

[stextbox id=’section’]Types of variables:[/stextbox]

Let’s categorize the possible variables to make the discussion easier and our analysis more structured. Following are the categories of variables we will discuss in this article :

1. Basic variable set

2. Derived variable set

3. Mathematically transformed variable set

4. Bin Variable set

5. Co-variant variable set

types_of_variables

Following is a business case we will consider for creating these variable sets :

Predict the total business of a insurance branch in next 3 months.

[stextbox id=”section”]1. Creating the basic variable set :  [/stextbox]

Get this step right and you are half done. There is no set procedure to get the right set of base variables. There are two approaches to get the set of exhaustive base variable set. Following are the approaches :

1. Create hypothesis which can possibly affect the  dependent variable (Here we don’t even care if the data for this variable is even available)

2. Enlist all variables available (Here we don’t even care if this variable can possibly affect the dependent variable)

Here, we try to find all possible variable which can be collected in the analysis without thinking of shortlisting them for the final model. Each of these hypothesis falls in one of the following 3 categories :

a. Demographic variables : These variable defines quantifiable statistics for a data-point.  In the current business case we will include variables like : Location of the branch, Number of Sales managers, Mix of designation in the branch etc.

b. Behavioral variables :  These variables comes from the past performance  of the subject. In the current case we will include variables like business done by branch in last quarter, Ticket size of the business done by branch, performance metrics of the sales managers in the branch.

c. Psychometric variables : For the current business case we will want to include variables like Net Promoter score of the branch, Employee satisfaction score of the branch etc. These types of variables which generally come from surveys are the psychometric variables.

[stextbox id=”section”]2. Creating the derived variable set :  [/stextbox]

 After completing the list of the basic variables we  move on to the derived variables. These variables have a better predictive power and are very stable. These variables are combination of more than one basic variable. Let’s see how can we form derived variables for the case in hand. Following are the possible variables :

a .Revenue generated per resource = Revenue of the branch / Number of sales managers

b. Revenue on investment of the branch = Revenue of the branch / Total Cost of branch

c. Vintage of the branch = Today’s date  – Date of branch opening

d. Ratio of Senior to Junior employee = # Senior employee/ # Junior employee

This list can go on. Try hard to create all possible combination which are expected to influence the dependent variable. For some more ideas on derived variables, read this article.

[stextbox id=”section”]3. Creating the Mathematically transformed set :  [/stextbox]

Till this step we already have all the basic and derived variables. Now is the time to find the best possible transformation for each of these variables. Try to check all possible mathematical transformation such as Sine, Cosine, Logarithmic, Exponential , Square, Square root etc. Once you have all the transformation for each of the variables, you have to choose the transformation that best mimics the dependent variable. This transformation should come from both business sense and statistical method. Following is what I do to choose the best transformation for each variable :

Make a regression model with only 2 steps (step-wise) and the actual dependent variable. Choose the transformation that enter the model in these 2 steps. Check if the transformation found as the best fit makes business sense and use it in the final model. For the current problem in hand Log(Total Revenue) is possibly a better variable than Total Revenue as the marginal addition on prediction will go down as the total revenue increases.

[stextbox id=”section”]4. Creating the Bin Variable set :  [/stextbox]

 Creating bin variables is very essential in regression model. Find the bivariate plot between dependent variable and all other independent variables listed till now. Find the intervals where the relationship breaks in the bivariate. For the case in hand, lets say the performance of the branch is best if “Ratio of Senior to Junior employee” is between 0.9 to 1.1 . In such case we will create a bin variable between 0.9 and 1.1. It will look like as follows :

Bin = 1    for    0.9 <Ratio < 1.1

Bin = 0    otherwise

We will include this bin variable in the regression model.

[stextbox id=”section”]5. Creating the Co-variant variable set :  [/stextbox]

 Here comes the X-factor for our regression model. This step incorporate the best cuts of a CART model and significantly raises the prediction power of the regression model. For more details on this technique, please read this article.

[stextbox id=”section”]Next steps to complete the regression model :  [/stextbox]

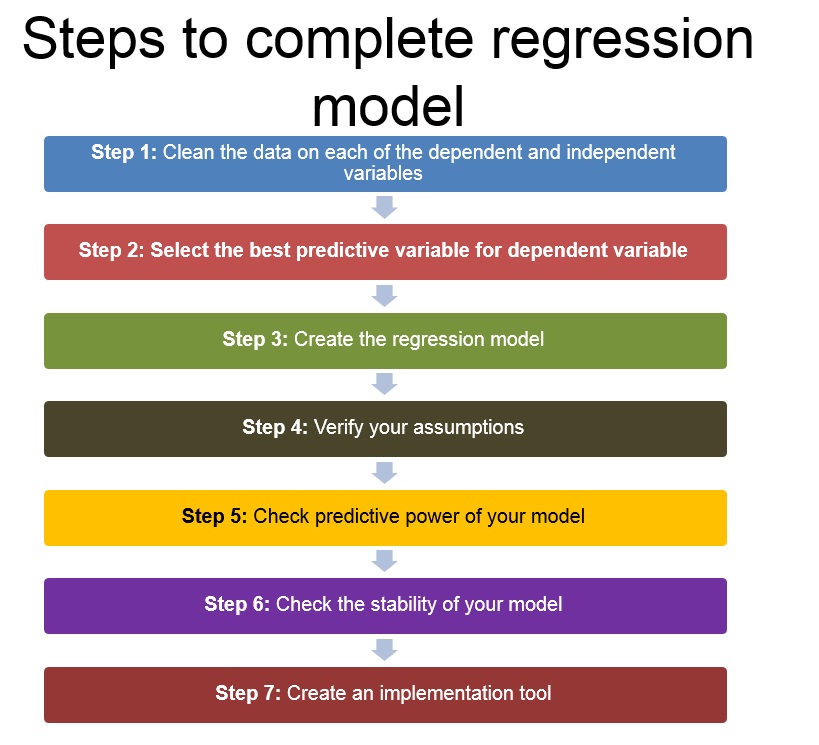
 After we are done with the variable collection, following is the order to complete the regression model :

1. Clean the data on each of the dependent and independent variables.

2. Select the best predictive variable for the dependent variable

3. Create the regression model

4. Check the assumptions of the regression model using diagnostic plots (for more details, read this article)

5. Check the predictive power of the model

6. Check the stability of the model

7. Create the implementation tool

steps_regression_model

[stextbox id=”section”]End notes :  [/stextbox]

The more exhaustive our starting hypothesis the better is the predictive power of the model.Did you find the article useful? Share with us any other variable sets you incorporate in your model.  Do let us know your thoughts about this article in the box below.

If you like what you just read & want to continue your analytics learning, subscribe to our emails or like our facebook page.

Tavish Srivastava
Tavish Srivastava

Tavish Srivastava, co-founder and Chief Strategy Officer of Analytics Vidhya, is an IIT Madras graduate and a passionate data-science professional with 8+ years of diverse experience in markets including the US, India and Singapore, domains including Digital Acquisitions, Customer Servicing and Customer Management, and industry including Retail Banking, Credit Cards and Insurance. He is fascinated by the idea of artificial intelligence inspired by human intelligence and enjoys every discussion, theory or even movie related to this idea.

Free Courses

Generative AI 4.7

Generative AI - A Way of Life

Explore Generative AI for beginners: create text and images, use top AI tools, learn practical skills, and ethics.
Large Language Models 4.5

Getting Started with Large Language Models

Master Large Language Models (LLMs) with this course, offering clear guidance in NLP and model training made simple.
Prompt Engineering 4.6

Building LLM Applications using Prompt Engineering

This free course guides you on building LLM apps, mastering prompt engineering, and developing chatbots with enterprise data.
LlamaIndex 4.8

Improving Real World RAG Systems: Key Challenges & Practical Solutions

Explore practical solutions, advanced retrieval strategies, and agentic RAG systems to improve context, relevance, and accuracy in AI-driven applications.
RAG systems using LlamaIndex 4.7

Microsoft Excel: Formulas & Functions

Master MS Excel for data analysis with key formulas, functions, and LookUp tools in this comprehensive course.

Recommended Articles

Responses From Readers

Clear

Rachit
Rachit

Hi Kunal, This article is helpful and gives structured understanding of Regression Model. I would also request you to explain these steps through a case study which can help us in understanding how we 1. clean data 2. select predictors (challenges of dummy variables in case of categorical variables). 3. Verify assumptions 4. Model Validation

123

Kunal Jain
Kunal Jain

Rachit, Thanks for the suggestion. Would cover this through one of the articles in coming days. Stay tuned! Thanks, Kunal

123
rohit
rohit

HI Kunal, Can you just give example of transformation of variables and how do we interpret this transformed variables. For example: Y=10 Log(x1)+1000/(x2)+100 sqrt(x3) And also how should we decide which tranformation goes in favour of our model. Thanks, Rohit

123

Tavish Srivastava
Tavish Srivastava

Rohit, When you have a transformed variable in your kitty, the relationship between x and y is no longer linear. Hence the interpretation of coefficient is made in terms of the transformed variable. In your example, a unit increase in the value of log x1 increases the value of y by 10. Coming to your second question, an easy way to choose transformed variables is to build a step wise regression model for all the transformed variables coming from one input variable and choose the final 2 variables entering the model. This makes sure that the cgi squared value of the transformed variable is high. If the original variable has a much higher chi squared value, the transformed variables will not add much value to your model. Hope this helps. Tavish

123
Arindam
Arindam

How do you interpret the trignometric function of independent var in business sense. Can you explain with an example. Thanks.

123

Write for us

Write, captivate, and earn accolades and rewards for your work
  • Reach a Global Audience
  • Get Expert Feedback
  • Build Your Brand & Audience
  • Cash In on Your Knowledge
  • Join a Thriving Community
  • Level Up Your Data Science Game
imag

We use cookies essential for this site to function well. Please click to help us improve its usefulness with additional cookies. Learn about our use of cookies in our Privacy Policy & Cookies Policy.

Show details